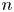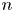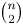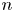Refine search
Actions for selected content:
4 results
On the distribution of winners’ scores in a round-robin tournament
- Part of
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 36 / Issue 4 / October 2022
- Published online by Cambridge University Press:
- 06 August 2021, pp. 1098-1102
-
- Article
- Export citation
Optimal and myopic search in a binary random vector
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 35 / Issue 2 / June 1998
- Published online by Cambridge University Press:
- 14 July 2016, pp. 463-472
- Print publication:
- June 1998
-
- Article
- Export citation
A new autoregressive time series model in exponential variables (NEAR(1))
-
- Journal:
- Advances in Applied Probability / Volume 13 / Issue 4 / December 1981
- Published online by Cambridge University Press:
- 01 July 2016, pp. 826-845
- Print publication:
- December 1981
-
- Article
- Export citation
The supremum distribution of another Gaussian process
-
- Journal:
- Journal of Applied Probability / Volume 18 / Issue 1 / March 1981
- Published online by Cambridge University Press:
- 14 July 2016, pp. 131-138
- Print publication:
- March 1981
-
- Article
- Export citation