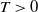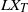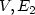Refine search
Actions for selected content:
36 results
Professional and part-time potters and painters: modelling the production of Athenian black- and red-figure painted pottery
-
- Journal:
- The Journal of Hellenic Studies , First View
- Published online by Cambridge University Press:
- 26 August 2025, pp. 1-22
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
11 - Numerical Simulations
-
- Book:
- Probability Theory for Quantitative Scientists
- Published online:
- 24 July 2025
- Print publication:
- 14 August 2025, pp 289-303
-
- Chapter
- Export citation
Doubly Robust-Type Estimation for Covariate Adjustment in Latent Variable Modeling
-
- Journal:
- Psychometrika / Volume 72 / Issue 4 / December 2007
- Published online by Cambridge University Press:
- 01 January 2025, pp. 535-549
-
- Article
- Export citation
5 - Computational Inference
- from Part I - Concepts from Modeling, Inference, and Computing
-
- Book:
- Data Modeling for the Sciences
- Published online:
- 17 August 2023
- Print publication:
- 31 August 2023, pp 163-212
-
- Chapter
- Export citation
5 - Review of Mathematical and Statistical Concepts
-
- Book:
- Data Science for the Geosciences
- Published online:
- 25 August 2023
- Print publication:
- 17 August 2023, pp 204-239
-
- Chapter
- Export citation
8 - Monte Carlo Methods
-
- Book:
- Liquid Crystals and their Computer Simulations
- Published online:
- 21 July 2022
- Print publication:
- 28 July 2022, pp 359-378
-
- Chapter
- Export citation
Comparison of the dose perturbation arising from conventional and the novel PEEK prosthesis materials during high energy radiotherapy with 15 MV photons
-
- Journal:
- Journal of Radiotherapy in Practice / Volume 22 / 2023
- Published online by Cambridge University Press:
- 30 September 2021, e17
-
- Article
- Export citation
Exact simulation for multivariate Itô diffusions
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 52 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 03 December 2020, pp. 1003-1034
- Print publication:
- December 2020
-
- Article
- Export citation
Modelling and inference of maize pollen emission rate with a Lagrangian dispersal model using Monte Carlo method
-
- Journal:
- The Journal of Agricultural Science / Volume 158 / Issue 5 / July 2020
- Published online by Cambridge University Press:
- 01 October 2020, pp. 383-395
-
- Article
- Export citation
Simulation of elliptic and hypo-elliptic conditional diffusions
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 52 / Issue 1 / March 2020
- Published online by Cambridge University Press:
- 29 April 2020, pp. 173-212
- Print publication:
- March 2020
-
- Article
- Export citation
A multilevel approach towards unbiased sampling of random elliptic partial differential equations
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 50 / Issue 4 / December 2018
- Published online by Cambridge University Press:
- 29 November 2018, pp. 1007-1031
- Print publication:
- December 2018
-
- Article
- Export citation
Estimating true incidence of O157 and non-O157 Shiga toxin-producing Escherichia coli illness in Germany based on notification data of haemolytic uraemic syndrome
-
- Journal:
- Epidemiology & Infection / Volume 144 / Issue 15 / November 2016
- Published online by Cambridge University Press:
- 29 July 2016, pp. 3305-3315
-
- Article
-
- You have access
- HTML
- Export citation
Optimal importance sampling for the Laplace transform of exponential Brownian functionals
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 53 / Issue 2 / June 2016
- Published online by Cambridge University Press:
- 21 June 2016, pp. 531-542
- Print publication:
- June 2016
-
- Article
- Export citation
An Implicit Algorithm of Solving Nonlinear Filtering Problems
-
- Journal:
- Communications in Computational Physics / Volume 16 / Issue 2 / August 2014
- Published online by Cambridge University Press:
- 03 June 2015, pp. 382-402
- Print publication:
- August 2014
-
- Article
- Export citation
Random Construction of Interpolating Sets for High-Dimensional Integration
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 51 / Issue 1 / March 2014
- Published online by Cambridge University Press:
- 30 January 2018, pp. 92-105
- Print publication:
- March 2014
-
- Article
-
- You have access
- Export citation
Gaskinetic Solutions for High Knudsen Number Planar Jet Impingement Flows
-
- Journal:
- Communications in Computational Physics / Volume 14 / Issue 4 / October 2013
- Published online by Cambridge University Press:
- 03 June 2015, pp. 960-978
- Print publication:
- October 2013
-
- Article
- Export citation
An improved derandomized approximation algorithmfor the max-controlledset problem
-
- Journal:
- RAIRO - Theoretical Informatics and Applications / Volume 45 / Issue 2 / April 2011
- Published online by Cambridge University Press:
- 28 February 2011, pp. 181-196
- Print publication:
- April 2011
-
- Article
- Export citation
Stochastic Monotonicity and Continuity Properties of the Extinction Time of Bellman-Harris Branching Processes: An Application to Epidemic Modelling
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 47 / Issue 1 / March 2010
- Published online by Cambridge University Press:
- 14 July 2016, pp. 58-71
- Print publication:
- March 2010
-
- Article
-
- You have access
- Export citation
Méthodologie d'analyse et d'optimisation des tolérances dans un contexte de conception intégrée : TOL_ANALYSES
-
- Journal:
- Mechanics & Industry / Volume 9 / Issue 5 / September 2008
- Published online by Cambridge University Press:
- 14 March 2009, pp. 381-395
- Print publication:
- September 2008
-
- Article
- Export citation