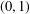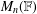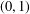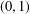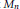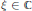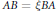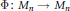Refine search
Actions for selected content:
10 results
1 - Introduction: A First Data Science Problem
-
- Book:
- Mathematical Methods in Data Science
- Published online:
- 04 November 2025
- Print publication:
- 30 October 2025, pp 1-66
-
- Chapter
- Export citation
2 - Least Squares: Geometric, Algebraic, and Numerical Aspects
-
- Book:
- Mathematical Methods in Data Science
- Published online:
- 04 November 2025
- Print publication:
- 30 October 2025, pp 67-127
-
- Chapter
- Export citation
A Theorem on the Rank of a Product of Matrices with Illustration of Its Use in Goodness of Fit Testing
-
- Journal:
- Psychometrika / Volume 80 / Issue 4 / December 2015
- Published online by Cambridge University Press:
- 01 January 2025, pp. 938-948
-
- Article
- Export citation

Time-Variant and Quasi-separable Systems
- Matrix Theory, Recursions and Computations
-
- Published online:
- 24 October 2024
- Print publication:
- 31 October 2024
2 - Review of Mathematics
-
- Book:
- Applied Hydrology
- Published online:
- 09 July 2024
- Print publication:
- 04 July 2024, pp 11-35
-
- Chapter
- Export citation
2 - Multimodal Graphs and Matrices
-
- Book:
- Multimodal Political Networks
- Published online:
- 12 May 2021
- Print publication:
- 27 May 2021, pp 20-52
-
- Chapter
- Export citation

Invitation to Linear Programming and Game Theory
-
- Published online:
- 11 March 2021
- Print publication:
- 11 March 2021
Appendix B - Notation
-
- Book:
- Statistics
- Published online:
- 11 June 2020
- Print publication:
- 08 November 2018, pp 727-740
-
- Chapter
- Export citation
ON MINIMAL SETS OF
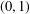 $(0,1)$ -MATRICES WHOSE PAIRWISE PRODUCTS FORM A BASIS FOR
$(0,1)$ -MATRICES WHOSE PAIRWISE PRODUCTS FORM A BASIS FOR 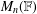 $M_{n}(\mathbb{F})$
$M_{n}(\mathbb{F})$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 98 / Issue 3 / December 2018
- Published online by Cambridge University Press:
- 28 August 2018, pp. 402-413
- Print publication:
- December 2018
-
- Article
-
- You have access
- Export citation
General Preservers of Quasi-Commutativity
-
- Journal:
- Canadian Journal of Mathematics / Volume 62 / Issue 4 / 01 August 2010
- Published online by Cambridge University Press:
- 20 November 2018, pp. 758-786
- Print publication:
- 01 August 2010
-
- Article
-
- You have access
- Export citation