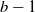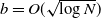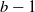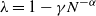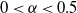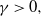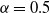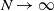Refine search
Actions for selected content:
2 results
Steady-state analysis of load-balancing algorithms in the sub-Halfin–Whitt regime
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 57 / Issue 2 / June 2020
- Published online by Cambridge University Press:
- 16 July 2020, pp. 578-596
- Print publication:
- June 2020
-
- Article
- Export citation
Staffing Many-Server Systems with Admission Control and Retrials
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 47 / Issue 2 / June 2015
- Published online by Cambridge University Press:
- 22 February 2016, pp. 450-475
- Print publication:
- June 2015
-
- Article
-
- You have access
- Export citation