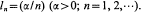In a coverage problem introduced by Dvoretzky (1956) the circle is covered with lengths The associated indexed martingale can be considered as a set of random densities with respect to Lebesgue measure, of which the limit is a random measure. The total masses of the set constitute a new martingale. From a theorem of Shepp (1972), this martingale does not converge in a space 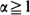if 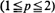. If 0 < α < 1 it converges in all spaces 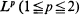, and in this paper we demonstrate that it converges in all spaces Lp for p > 2. We also obtain quite precise estimates for the moments of the total mass of the limit measure, showing that the characteristic function of this total mass is an entire function of order 1/(1 − α). Thus in some sense the mass is distributed in a bounded domain.

This paper presents some limit theorems for the simple branching process allowing immigration, {Xn }, when the offspring mean is infinite. It is shown that there exists a function U such that {e –n U/(Xn )} converges almost surely, and if s = ∑ bj , log+U(j) < ∞, where {bj } is the immigration distribution, the limit is non-defective and non-degenerate but is infinite if s = ∞.

When s = ∞, limit theorems are found for {U(Xn )} which involve a slowly varying non-linear norming.