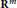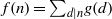Refine search
Actions for selected content:
2 results
Differential-free Characterisation of Smooth Mappings with Controlled Growth
-
- Journal:
- Canadian Mathematical Bulletin / Volume 61 / Issue 3 / 01 September 2018
- Published online by Cambridge University Press:
- 20 November 2018, pp. 628-636
- Print publication:
- 01 September 2018
-
- Article
-
- You have access
- Export citation
UNCERTAINTY PRINCIPLES CONNECTED WITH THE MÖBIUS INVERSION FORMULA
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 88 / Issue 3 / December 2013
- Published online by Cambridge University Press:
- 25 January 2013, pp. 460-472
- Print publication:
- December 2013
-
- Article
-
- You have access
- Export citation