Refine search
Actions for selected content:
2 results
The depletion time for M/G/1 systems and a related limit theorem
-
- Journal:
- Advances in Applied Probability / Volume 15 / Issue 2 / June 1983
- Published online by Cambridge University Press:
- 01 July 2016, pp. 420-443
- Print publication:
- June 1983
-
- Article
- Export citation
The covariance function of the virtual waiting-time process in an M/G/1 queue
-
- Journal:
- Advances in Applied Probability / Volume 9 / Issue 1 / March 1977
- Published online by Cambridge University Press:
- 01 July 2016, pp. 158-168
- Print publication:
- March 1977
-
- Article
- Export citation
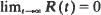 and
and  if and only if the service-times have a finite fourth moment.
if and only if the service-times have a finite fourth moment.