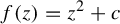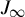Refine search
Actions for selected content:
21 results
A NEW PROOF OF THE SINGULAR CONTINUITY OF THE MINKOWSKI
 $?$-FUNCTION
$?$-FUNCTION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 04 December 2025, pp. 1-6
-
- Article
- Export citation
Topological and smooth classification of Anosov maps on torus
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 10 / October 2025
- Published online by Cambridge University Press:
- 15 December 2025, pp. 2603-2653
- Print publication:
- October 2025
-
- Article
- Export citation
Semisimple random walks on the torus
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 10 / October 2025
- Published online by Cambridge University Press:
- 03 March 2025, pp. 3090-3147
- Print publication:
- October 2025
-
- Article
- Export citation
Asymptotic expansion of the invariant measure for Markov-modulated ODEs at high frequency
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 62 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 30 January 2025, pp. 898-924
- Print publication:
- September 2025
-
- Article
- Export citation
On invariant measures of ‘satellite’ infinitely renormalizable quadratic polynomials
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 6 / June 2025
- Published online by Cambridge University Press:
- 13 November 2024, pp. 1843-1869
- Print publication:
- June 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On bifurcation of statistical properties of partially hyperbolic endomorphisms
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 3 / March 2024
- Published online by Cambridge University Press:
- 18 April 2023, pp. 933-944
- Print publication:
- March 2024
-
- Article
- Export citation
Appendix
-
- Book:
- Transport Barriers and Coherent Structures in Flow Data
- Published online:
- 20 February 2023
- Print publication:
- 16 March 2023, pp 367-389
-
- Chapter
- Export citation
A QUANTITATIVE EVALUATION OF LAGRANGIAN COHERENT STRUCTURE DETECTION METHODS BASED ON COMPUTATIONAL AND EXPERIMENTAL LIMITATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 107 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 05 December 2022, pp. 173-174
- Print publication:
- February 2023
-
- Article
-
- You have access
- HTML
- Export citation
10 - Dynamics and Data Assimilation
- from Part III - Methods and Issues
-
- Book:
- Principles of Data Assimilation
- Published online:
- 22 September 2022
- Print publication:
- 29 September 2022, pp 251-262
-
- Chapter
- Export citation
13 - Transport in Hamiltonian Dynamical Models
-
- Book:
- The Statistical Mechanics of Irreversible Phenomena
- Published online:
- 14 July 2022
- Print publication:
- 28 July 2022, pp 469-493
-
- Chapter
- Export citation
Absolute continuity, Lyapunov exponents, and rigidity II: systems with compact center leaves
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 2 / February 2022
- Published online by Cambridge University Press:
- 31 May 2021, pp. 437-490
- Print publication:
- February 2022
-
- Article
- Export citation
Margulis–Ruelle inequality for general manifolds
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 6 / June 2022
- Published online by Cambridge University Press:
- 22 April 2021, pp. 2064-2079
- Print publication:
- June 2022
-
- Article
- Export citation
14 - Complex Systems
- from Part III
-
- Book:
- Modern Classical Mechanics
- Published online:
- 30 November 2020
- Print publication:
- 10 December 2020, pp 575-616
-
- Chapter
- Export citation
Effective multi-scale approach to the Schrödinger cocycle over a skew-shift base
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 10 / October 2020
- Published online by Cambridge University Press:
- 17 April 2019, pp. 2788-2853
- Print publication:
- October 2020
-
- Article
- Export citation
Numerical Modeling of Material Points Evolution in a System with Gravity
-
- Journal:
- Communications in Computational Physics / Volume 21 / Issue 4 / April 2017
- Published online by Cambridge University Press:
- 08 March 2017, pp. 1118-1140
- Print publication:
- April 2017
-
- Article
- Export citation
LONG-RUN OPTIMAL BEHAVIOR IN A TWO-SECTOR ROBINSON–SOLOW–SRINIVASAN MODEL
-
- Journal:
- Macroeconomic Dynamics / Volume 16 / Issue S1 / April 2012
- Published online by Cambridge University Press:
- 05 December 2011, pp. 70-85
-
- Article
- Export citation
Asymptotic Stability of Stochastic Differential Equations Driven by Lévy Noise
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 46 / Issue 4 / December 2009
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1116-1129
- Print publication:
- December 2009
-
- Article
-
- You have access
- Export citation
ABSENCE OF CHAOS AND 1/f SPECTRA, BUT EVIDENCE OF TAR NONLINEARITIES, IN THE CANADIAN EXCHANGE RATE
-
- Journal:
- Macroeconomic Dynamics / Volume 8 / Issue 4 / September 2004
- Published online by Cambridge University Press:
- 01 September 2004, pp. 543-551
-
- Article
- Export citation
Particle approximations of Lyapunov exponents connected to Schrödinger operators and Feynman–Kac semigroups
-
- Journal:
- ESAIM: Probability and Statistics / Volume 7 / March 2003
- Published online by Cambridge University Press:
- 15 May 2003, pp. 171-208
- Print publication:
- March 2003
-
- Article
- Export citation
Stability index for products of random transformations
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 30 / Issue 4 / December 1998
- Published online by Cambridge University Press:
- 01 July 2016, pp. 968-988
- Print publication:
- December 1998
-
- Article
- Export citation