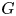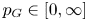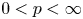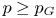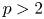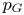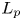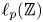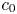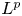Refine search
Actions for selected content:
4 results
Isometric actions on Lp-spaces: dependence on the value of p
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 6 / June 2023
- Published online by Cambridge University Press:
- 26 May 2023, pp. 1300-1313
- Print publication:
- June 2023
-
- Article
- Export citation
Chaos and frequent hypercyclicity for composition operators
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 3 / August 2021
- Published online by Cambridge University Press:
- 04 June 2021, pp. 513-531
-
- Article
- Export citation
16 - Applications in Functional Analysis
- from Part Three - Applications
-
- Book:
- Assouad Dimension and Fractal Geometry
- Published online:
- 13 October 2020
- Print publication:
- 29 October 2020, pp 230-236
-
- Chapter
- Export citation
AN ARBITRARY INTERSECTION OF Lp-SPACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 85 / Issue 3 / June 2012
- Published online by Cambridge University Press:
- 16 February 2012, pp. 433-445
- Print publication:
- June 2012
-
- Article
-
- You have access
- Export citation