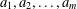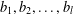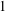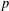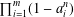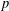Refine search
Actions for selected content:
1 results
NOTE ON LEHMER–PIERCE SEQUENCES WITH THE SAME PRIME DIVISORS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 97 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 04 October 2017, pp. 11-14
- Print publication:
- February 2018
-
- Article
-
- You have access
- Export citation