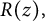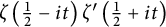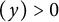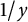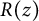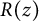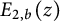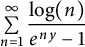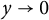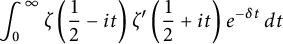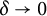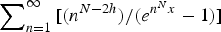Refine search
Actions for selected content:
5 results
Lambert series of logarithm, the derivative of Deninger’s function
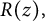 $R(z),$ and a mean value theorem for
$R(z),$ and a mean value theorem for 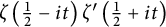 $\zeta \left (\frac {1}{2}-it\right )\zeta '\left (\frac {1}{2}+it\right )$
$\zeta \left (\frac {1}{2}-it\right )\zeta '\left (\frac {1}{2}+it\right )$
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 5 / October 2024
- Published online by Cambridge University Press:
- 11 October 2023, pp. 1695-1730
- Print publication:
- October 2024
-
- Article
- Export citation
Generalized Lambert series and arithmetic nature of odd zeta values
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 24 January 2019, pp. 741-769
- Print publication:
- April 2020
-
- Article
- Export citation
ELEMENTARY PROOFS OF VARIOUS FACTS ABOUT 3-CORES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 79 / Issue 3 / June 2009
- Published online by Cambridge University Press:
- 17 April 2009, pp. 507-512
- Print publication:
- June 2009
-
- Article
-
- You have access
- Export citation
ON THE NUMBER OF REPRESENTATIONS OF INTEGERS BY CERTAIN QUADRATIC FORMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 78 / Issue 1 / August 2008
- Published online by Cambridge University Press:
- 01 August 2008, pp. 129-140
- Print publication:
- August 2008
-
- Article
-
- You have access
- Export citation
Generalized Lambert series identities
-
- Journal:
- Proceedings of the London Mathematical Society / Volume 91 / Issue 3 / November 2005
- Published online by Cambridge University Press:
- 19 October 2005, pp. 598-622
- Print publication:
- November 2005
-
- Article
- Export citation