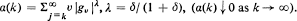Let {Zt ; t = 0, ± 1, ···} be a pure white noise process with γ = E{|Z 1 | δ}< ∞ for some δ > 0. Assume that the characteristic function (ch.f.) ϕ 0 of Z 1 is Lebesgue-integrable over (—∞, ∞). Let {gv ;v = 0, 1, 2, ···, g 0 = 1} be a sequence of real numbers such that 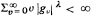 where λ = δ(1 + δ)−1. Define
where λ = δ(1 + δ)−1. Define 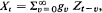 , where the identity is to be understood in the sense of convergence in distribution. Then {Xt ; t = 0, ± 1, ···} is a strongly mixing stationary process in the sense that if
, where the identity is to be understood in the sense of convergence in distribution. Then {Xt ; t = 0, ± 1, ···} is a strongly mixing stationary process in the sense that if 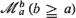 is the σ-fìeld generated by the random variables (r.v.) Xa , ···, Xb then for any
is the σ-fìeld generated by the random variables (r.v.) Xa , ···, Xb then for any 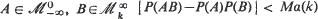 where M is a finite positive constant which depends only on ϕ 0 and
where M is a finite positive constant which depends only on ϕ 0 and 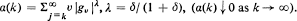
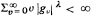 where
where 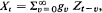 , where the identity is to be understood in the sense of convergence in distribution. Then {
, where the identity is to be understood in the sense of convergence in distribution. Then {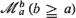 is the
is the 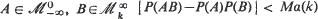 where
where