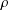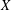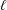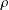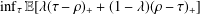Refine search
Actions for selected content:
5 results
Last exit time until first exit time for spectrally negative Lévy processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 62 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 24 January 2025, pp. 876-897
- Print publication:
- September 2025
-
- Article
- Export citation
On first exit times and their means for Brownian bridges
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 56 / Issue 3 / September 2019
- Published online by Cambridge University Press:
- 01 October 2019, pp. 701-722
- Print publication:
- September 2019
-
- Article
- Export citation
OPTIMAL STOPPING FOR THE LAST EXIT TIME
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 99 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 04 October 2018, pp. 148-160
- Print publication:
- February 2019
-
- Article
-
- You have access
- Export citation
On the last exit times for spectrally negative Lévy processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 54 / Issue 2 / June 2017
- Published online by Cambridge University Press:
- 22 June 2017, pp. 474-489
- Print publication:
- June 2017
-
- Article
- Export citation
Dynamic bandwidth allocation for ATM switches
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 33 / Issue 3 / September 1996
- Published online by Cambridge University Press:
- 14 July 2016, pp. 758-771
- Print publication:
- September 1996
-
- Article
- Export citation