Inner contact probabilities for convex bodies
-
- Journal:
- Advances in Applied Probability / Volume 14 / Issue 3 / September 1982
- Published online by Cambridge University Press:
- 01 July 2016, pp. 582-599
- Print publication:
- September 1982
-
- Article
- Export citation

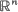 where
where 
