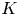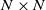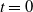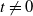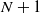Refine search
Actions for selected content:
11 results
The formation of a soliton gas condensate for the focusing nonlinear Schrödinger equation
-
- Journal:
- Journal of Nonlinear Waves / Volume 1 / 2025
- Published online by Cambridge University Press:
- 09 October 2025, e14
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Integrable fractional Burgers hierarchy
-
- Journal:
- Journal of Nonlinear Waves / Volume 1 / 2025
- Published online by Cambridge University Press:
- 31 July 2025, e3
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Locality of relative symplectic cohomology for complete embeddings
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 12 / December 2023
- Published online by Cambridge University Press:
- 10 October 2023, pp. 2551-2637
- Print publication:
- December 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the moments of characteristic polynomials
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue S1 / May 2023
- Published online by Cambridge University Press:
- 05 August 2022, pp. S102-S122
- Print publication:
- May 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
2 - The WKB Method and Nonperturbative Effects
-
- Book:
- Advanced Topics in Quantum Mechanics
- Published online:
- 02 December 2021
- Print publication:
- 09 December 2021, pp 31-113
-
- Chapter
- Export citation
14 - From Partial Differential Equations to Groups
-
-
- Book:
- Analysis and Geometry on Graphs and Manifolds
- Published online:
- 14 August 2020
- Print publication:
- 20 August 2020, pp 368-381
-
- Chapter
- Export citation
8 - The Rigid Body Dynamics in an Ideal Fluid: Clebsch Top and Kummer Surfaces
-
-
- Book:
- Integrable Systems and Algebraic Geometry
- Published online:
- 19 March 2020
- Print publication:
- 02 March 2020, pp 288-312
-
- Chapter
- Export citation
5 - First Integrals and Integrable Systems
-
- Book:
- A Comprehensive Introduction to Sub-Riemannian Geometry
- Published online:
- 28 October 2019
- Print publication:
- 31 October 2019, pp 149-170
-
- Chapter
- Export citation
SEMI-ABELIAN SURFACES AND INTEGRABLE SYSTEMS
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 44 / Issue 2 / June 2001
- Published online by Cambridge University Press:
- 20 January 2009, pp. 249-265
-
- Article
-
- You have access
- Export citation
A rigidity theorem for Lagrangian deformations
-
- Journal:
- Compositio Mathematica / Volume 141 / Issue 6 / November 2005
- Published online by Cambridge University Press:
- 04 December 2007, pp. 1602-1614
- Print publication:
- November 2005
-
- Article
-
- You have access
- Export citation
Hamiltonian stationary tori in the complex projective plane
-
- Journal:
- Proceedings of the London Mathematical Society / Volume 90 / Issue 2 / March 2005
- Published online by Cambridge University Press:
- 25 February 2005, pp. 472-496
- Print publication:
- March 2005
-
- Article
- Export citation