Given an integral functional defined on 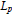 ${{L}_{p}}$,
${{L}_{p}}$, 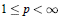 $1\le p<\infty $, under a growth condition we give an upper bound of the Clarke directional derivative and we obtain a nice inclusion between the Clarke subdifferential of the integral functional and the set of selections of the subdifferential of the integrand.
$1\le p<\infty $, under a growth condition we give an upper bound of the Clarke directional derivative and we obtain a nice inclusion between the Clarke subdifferential of the integral functional and the set of selections of the subdifferential of the integrand.