Given a quiver with potential 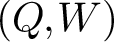(Q,W)$(Q,W)$, Kontsevich–Soibelman constructed a cohomological Hall algebra (CoHA) on the critical cohomology of the stack of representations of 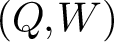(Q,W)$(Q,W)$. Special cases of this construction are related to work of Nakajima, Varagnolo, Schiffmann–Vasserot, Maulik–Okounkov, Yang–Zhao, etc. about geometric constructions of Yangians and their representations; indeed, given a quiver Q, there exists an associated pair 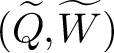(\widetilde{Q}, \widetilde{W})$(\widetilde{Q}, \widetilde{W})$ whose CoHA is conjecturally the positive half of the Maulik–Okounkov Yangian 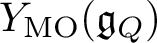Y_{\text {MO}}(\mathfrak {g}_{Q})$Y_{\text {MO}}(\mathfrak {g}_{Q})$.

For a quiver with potential 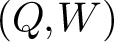(Q,W)$(Q,W)$, we follow a suggestion of Kontsevich–Soibelman and study a categorification of the above algebra constructed using categories of singularities. Its Grothendieck group is a K-theoretic Hall algebra (KHA) for quivers with potential. We construct representations using framed quivers, and we prove a wall-crossing theorem for KHAs. We expect the KHA for 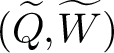(\widetilde{Q}, \widetilde{W})$(\widetilde{Q}, \widetilde{W})$ to recover the positive part of quantum affine algebra 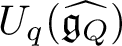U_{q}(\widehat {\mathfrak {g}_{Q}})$U_{q}(\widehat {\mathfrak {g}_{Q}})$ defined by Okounkov–Smirnov.

We study the derived Hall algebra of the partially wrapped Fukaya category of a surface. We give an explicit description of the Hall algebra for the disk with m$m$ marked intervals and we give a conjectural description of the Hall algebras of all surfaces with enough marked intervals. Then we use a functoriality result to show that a graded version of the HOMFLY-PT skein relation holds among certain arcs in the Hall algebras of general surfaces.

We give an explicit construction of the cusp eigenforms on an elliptic curve defined over a finite field, using the theory of Hall algebras and the Langlands correspondence for function fields and {\mathrm{GL} }_{n} ${\mathrm{GL} }_{n}$. As a consequence we obtain a description of the Hall algebra of an elliptic curve as an infinite tensor product of simpler algebras. We prove that all these algebras are specializations of a universal spherical Hall algebra (as defined and studied by Burban and Schiffmann  [On the Hall algebra of an elliptic curve I, Preprint (2005), arXiv:math/0505148 [math.AG]] and Schiffmann and Vasserot [The elliptic Hall algebra, Cherednik Hecke algebras and Macdonald polynomials, Compositio Math. 147 (2011), 188–234]).

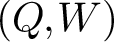
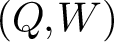
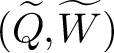
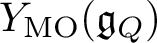
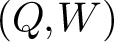
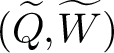
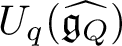
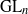
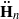We exhibit a strong link between the Hall algebra HX of an elliptic curve X defined over a finite field 𝔽l (or, more precisely, its spherical subalgebra U+X) and Cherednik’s double affine Hecke algebras of type GLn, for all n. This allows us to obtain a geometric construction of the Macdonald polynomials Pλ(q,t−1) in terms of certain functions (Eisenstein series) on the moduli space of semistable vector bundles on the elliptic curve X.

A factorization formula for certain automorphisms of a Poisson algebra associated with a quiver is proved, which involves framed versions of moduli spaces of quiver representations. This factorization formula is related to wall-crossing formulae for Donaldson–Thomas type invariants of Kontsevich and Soibelman.