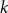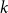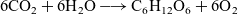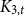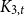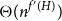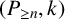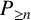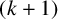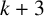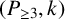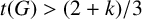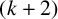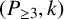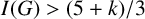Refine search
Actions for selected content:
54 results
13 - Financial networks
-
- Book:
- Financial Data Science
- Published online:
- 17 December 2025
- Print publication:
- 17 July 2025, pp 337-370
-
- Chapter
- Export citation
1 - Making and Recognizing Networks
- from Part I - A Brief Guide to Network Science
-
- Book:
- Behavioral Network Science
- Published online:
- 08 November 2024
- Print publication:
- 19 December 2024, pp 11-23
-
- Chapter
- Export citation
1 - Introduction
-
- Book:
- Understanding Visuals in the Life Sciences
- Published online:
- 31 October 2024
- Print publication:
- 21 November 2024, pp 1-18
-
- Chapter
-
- You have access
- HTML
- Export citation
4 - Illustrations
-
- Book:
- Understanding Visuals in the Life Sciences
- Published online:
- 31 October 2024
- Print publication:
- 21 November 2024, pp 68-93
-
- Chapter
- Export citation
3 - Micrographs
-
- Book:
- Understanding Visuals in the Life Sciences
- Published online:
- 31 October 2024
- Print publication:
- 21 November 2024, pp 43-67
-
- Chapter
- Export citation
6 - Interactive Visuals
-
- Book:
- Understanding Visuals in the Life Sciences
- Published online:
- 31 October 2024
- Print publication:
- 21 November 2024, pp 125-152
-
- Chapter
- Export citation
7 - Infographics
-
- Book:
- Understanding Visuals in the Life Sciences
- Published online:
- 31 October 2024
- Print publication:
- 21 November 2024, pp 153-181
-
- Chapter
- Export citation
5 - Graphs
-
- Book:
- Understanding Visuals in the Life Sciences
- Published online:
- 31 October 2024
- Print publication:
- 21 November 2024, pp 94-124
-
- Chapter
- Export citation
2 - Photographs
-
- Book:
- Understanding Visuals in the Life Sciences
- Published online:
- 31 October 2024
- Print publication:
- 21 November 2024, pp 19-42
-
- Chapter
- Export citation

Understanding Visuals in the Life Sciences
-
- Published online:
- 31 October 2024
- Print publication:
- 21 November 2024
Chapter One - Introduction to Data in Research
-
- Book:
- Understanding Figures in Neuroscience Research
- Published online:
- 22 November 2024
- Print publication:
- 13 June 2024, pp 1-25
-
- Chapter
- Export citation
A novel approach towards utilizing graph analyzing objects arrangement – case studies from Airbnb homes in New York and Boston
-
- Journal:
- Proceedings of the Design Society / Volume 4 / May 2024
- Published online by Cambridge University Press:
- 16 May 2024, pp. 175-184
-
- Article
-
- You have access
- Open access
- Export citation
The digital thread for system lifecycle management with a native graph database in a polyglot architecture
-
- Journal:
- Proceedings of the Design Society / Volume 4 / May 2024
- Published online by Cambridge University Press:
- 16 May 2024, pp. 2079-2088
-
- Article
-
- You have access
- Open access
- Export citation
COMPUTABLE VS DESCRIPTIVE COMBINATORICS OF LOCAL PROBLEMS ON TREES
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 89 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 04 July 2023, pp. 1835-1849
- Print publication:
- December 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Clustered colouring of graph classes with bounded treedepth or pathwidth
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 05 July 2022, pp. 122-133
-
- Article
- Export citation
On the sum of chemical reactions
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 34 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 24 May 2022, pp. 303-325
-
- Article
- Export citation
Subgraph densities in a surface
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 31 / Issue 5 / September 2022
- Published online by Cambridge University Press:
- 11 January 2022, pp. 812-839
-
- Article
- Export citation
TOUGHNESS, ISOLATED TOUGHNESS AND PATH FACTORS IN GRAPHS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 2 / October 2022
- Published online by Cambridge University Press:
- 03 December 2021, pp. 195-202
- Print publication:
- October 2022
-
- Article
- Export citation
2 - Mixed-Integer Programming
- from Part I - Background
-
- Book:
- Chemical Production Scheduling
- Published online:
- 01 May 2021
- Print publication:
- 06 May 2021, pp 32-64
-
- Chapter
- Export citation
7 - The Graph Conception
-
- Book:
- Conceptions of Set and the Foundations of Mathematics
- Published online:
- 09 January 2020
- Print publication:
- 23 January 2020, pp 184-217
-
- Chapter
- Export citation