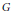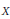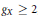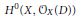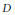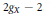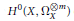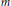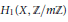Refine search
Actions for selected content:
1 results
Faithfulness of Actions on Riemann-Roch Spaces
-
- Journal:
- Canadian Journal of Mathematics / Volume 67 / Issue 4 / 01 August 2015
- Published online by Cambridge University Press:
- 20 November 2018, pp. 848-869
- Print publication:
- 01 August 2015
-
- Article
-
- You have access
- Export citation
-
Given a faithful action of a finite group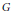
$G$ on an algebraic curve 
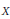$X$ of genus 
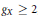$gx\,\ge \,2$ , we give explicit criteria for the induced action of 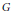$G$ on the Riemann–Roch space 
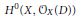${{H}^{0}}\left( X,\,{{\mathcal{O}}_{X}}\left( D \right) \right)$ to be faithful, where 
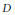$D$ is a 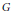$G$ -invariant divisor on 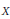$X$ of degree at least 
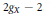${{2}_{gX}}\,-\,2$ . This leads to a concise answer to the question of when the action of 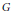$G$ on the space 
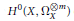${{H}^{0}}\left( X,\,\Omega _{X}^{\otimes m} \right)$ of global holomorphic polydifferentials of order 
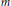$m$ is faithful. If 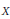$X$ is hyperelliptic, we provide an explicit basis of 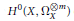${{H}^{0}}\left( X,\,\Omega _{X}^{\otimes m} \right)$ . Finally, we give applications in deformation theory and in coding theory and discuss the analogous problem for the action of 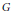$G$ on the first homology 
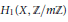${{H}_{1}}\left( X,\,\mathbb{Z}/m\mathbb{Z} \right)$ if 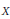$X$ is a Riemann surface.
