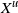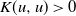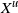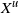Refine search
Actions for selected content:
3 results
Couplings for determinantal point processes and their reduced Palm distributions with a view to quantifying repulsiveness
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 58 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 23 June 2021, pp. 469-483
- Print publication:
- June 2021
-
- Article
- Export citation
A note on the simulation of the Ginibre point process
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 52 / Issue 4 / December 2015
- Published online by Cambridge University Press:
- 30 March 2016, pp. 1003-1012
- Print publication:
- December 2015
-
- Article
-
- You have access
- Export citation
A Cellular Network Model with Ginibre Configured Base Stations
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 46 / Issue 3 / September 2014
- Published online by Cambridge University Press:
- 22 February 2016, pp. 832-845
- Print publication:
- September 2014
-
- Article
-
- You have access
- Export citation