We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
In this paper, we prove the global null controllability ofthe linear heat equation completed with linear Fourierboundary conditions of the form ${\partial y\over\partial n} + \beta\,y = 0$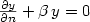 
. We consider distributed controls with support in a small set andnonregular coefficients $\beta=\beta(x,t)$ 
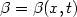. For the proof of null controllability, a crucial tool will be a new Carleman estimate for the weak solutions of the classical heatequation with nonhomogeneous Neumann boundary conditions.
