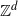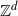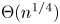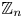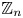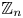Refine search
Actions for selected content:
35 results
Time series analysis of nuptial flights of Afrotropical ants (Hymenoptera: Formicidae), and the influence of moonlight on catches
-
- Journal:
- Bulletin of Entomological Research / Volume 115 / Issue 3 / June 2025
- Published online by Cambridge University Press:
- 31 March 2025, pp. 386-402
-
- Article
- Export citation
10 - Fourier Analysis
- from Part II - Mathematical Methods
-
- Book:
- An Introduction to Continuum Physics
- Published online:
- 06 February 2025
- Print publication:
- 13 February 2025, pp 519-569
-
- Chapter
- Export citation
X-Ray Powder Diffraction Studies on the Rehydration Properties of Beidellite
-
- Journal:
- Clays and Clay Minerals / Volume 39 / Issue 1 / February 1991
- Published online by Cambridge University Press:
- 02 April 2024, pp. 77-83
-
- Article
- Export citation
Interaction of Vermiculite with Aliphatic Amides (Formamide, Acetamide and Propionamide): Formation and Study of Interstratified Phases in the Transformation of Mg- to NH4-Vermiculite
-
- Journal:
- Clays and Clay Minerals / Volume 45 / Issue 3 / June 1997
- Published online by Cambridge University Press:
- 28 February 2024, pp. 311-326
-
- Article
- Export citation
Experimental Determinations of the Coherent Scattering Domain Size Distribution of Natural Mica-Like Phases with the Warren-Averbach Technique
-
- Journal:
- Clays and Clay Minerals / Volume 42 / Issue 4 / August 1994
- Published online by Cambridge University Press:
- 28 February 2024, pp. 489-494
-
- Article
- Export citation
11 - Time Series
-
- Book:
- Introduction to Environmental Data Science
- Published online:
- 23 March 2023
- Print publication:
- 23 March 2023, pp 372-417
-
- Chapter
- Export citation
2 - Linear Invariant Systems and Fourier Analysis
-
- Book:
- Modern Information Optics with MATLAB
- Published online:
- 22 December 2022
- Print publication:
- 05 January 2023, pp 21-69
-
- Chapter
- Export citation
Local limit theorem for a Markov additive process on
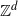 $\mathbb{Z}^d$ with a null recurrent internal Markov chain
$\mathbb{Z}^d$ with a null recurrent internal Markov chain
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 22 December 2022, pp. 570-588
- Print publication:
- June 2023
-
- Article
- Export citation
Discrepancy in modular arithmetic progressions
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 11 / November 2022
- Published online by Cambridge University Press:
- 01 December 2022, pp. 2082-2108
- Print publication:
- November 2022
-
- Article
- Export citation
Appendix D - Waves and Fourier Analysis
-
- Book:
- Quantum Mechanics
- Published online:
- 11 February 2023
- Print publication:
- 15 September 2022, pp 541-546
-
- Chapter
- Export citation
16 - More Discussion on the Harmonic Analysis and Fourier Analysis
-
- Book:
- Time Series Data Analysis in Oceanography
- Published online:
- 21 April 2022
- Print publication:
- 05 May 2022, pp 279-307
-
- Chapter
- Export citation
Appendix C - Fourier Series and Fourier Integrals
-
- Book:
- A Short Introduction to String Theory
- Published online:
- 31 March 2022
- Print publication:
- 07 April 2022, pp 242-243
-
- Chapter
- Export citation
18 - Stellar Rotation
-
- Book:
- The Observation and Analysis of Stellar Photospheres
- Published online:
- 05 January 2022
- Print publication:
- 16 December 2021, pp 439-487
-
- Chapter
- Export citation
17 - Velocity Fields in Stellar Photospheres
-
- Book:
- The Observation and Analysis of Stellar Photospheres
- Published online:
- 05 January 2022
- Print publication:
- 16 December 2021, pp 392-438
-
- Chapter
- Export citation
3 - Wavelength Modulation Spectroscopy with DFB Lasers
-
- Book:
- Laser and Fiber Optic Gas Absorption Spectroscopy
- Published online:
- 07 April 2021
- Print publication:
- 08 April 2021, pp 53-84
-
- Chapter
- Export citation
Fourier analysis using the number of COVID-19 daily deaths in the US
-
- Journal:
- Epidemiology & Infection / Volume 149 / 2021
- Published online by Cambridge University Press:
- 04 March 2021, e64
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
7 - Polymath’s Refinements of Maynards Results
-
- Book:
- Bounded Gaps Between Primes
- Published online:
- 10 September 2021
- Print publication:
- 25 February 2021, pp 272-326
-
- Chapter
- Export citation
Variability Predictors of Vasospasm in Subarachnoid Hemorrhage: A Feasibility Study
-
- Journal:
- Canadian Journal of Neurological Sciences / Volume 48 / Issue 2 / March 2021
- Published online by Cambridge University Press:
- 20 July 2020, pp. 226-232
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
4 - Small Doubling in Abelian Groups
-
- Book:
- Introduction to Approximate Groups
- Published online:
- 31 October 2019
- Print publication:
- 14 November 2019, pp 54-80
-
- Chapter
- Export citation
1 - What Is Fourier Analysis?
-
- Book:
- A Primer on Fourier Analysis for the Geosciences
- Published online:
- 01 February 2019
- Print publication:
- 14 February 2019, pp 1-8
-
- Chapter
- Export citation