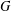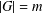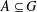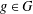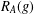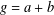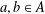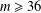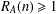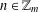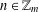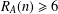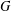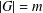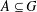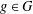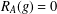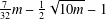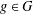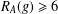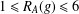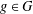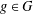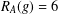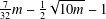For any finite abelian group 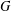$G$ with 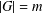$|G|=m$ , 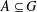$A\subseteq G$ and 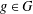$g\in G$ , let 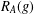$R_{A}(g)$ be the number of solutions of the equation 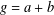$g=a+b$ , 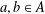$a,b\in A$ . Recently, Sándor and Yang [‘A lower bound of Ruzsa’s number related to the Erdős–Turán conjecture’, Preprint, 2016, arXiv:1612.08722v1] proved that, if 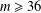$m\geq 36$ and 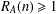$R_{A}(n)\geq 1$ for all 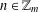$n\in \mathbb{Z}_{m}$ , then there exists 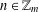$n\in \mathbb{Z}_{m}$ such that 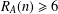$R_{A}(n)\geq 6$ . In this paper, for any finite abelian group 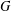$G$ with 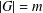$|G|=m$ and 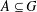$A\subseteq G$ , we prove that (a) if the number of 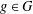$g\in G$ with 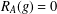$R_{A}(g)=0$ does not exceed 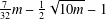$\frac{7}{32}m-\frac{1}{2}\sqrt{10m}-1$ , then there exists 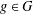$g\in G$ such that 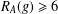$R_{A}(g)\geq 6$ ; (b) if 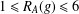$1\leq R_{A}(g)\leq 6$ for all 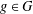$g\in G$ , then the number of 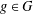$g\in G$ with 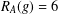$R_{A}(g)=6$ is more than 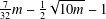$\frac{7}{32}m-\frac{1}{2}\sqrt{10m}-1$ .

Let σA(n)=∣{(a,a′)∈A2:a+a′=n}∣, where n∈ℕ and A is a subset of ℕ. Erdős and Turán con-jectured that for any basis A of ℕ, σA(n) is unbounded. In 1990, Ruzsa constructed a basis A⊂ℕ for which σA(n) is bounded in square mean. Based on Ruzsa’s method, we proved that there exists a basis A of ℕ satisfying ∑ n≤Nσ2A(n)≤1449757928N for large enough N. In this paper, we give a quantitative result for the existence of N, that is, we show that there exists a basis A of ℕ satisfying ∑ n≤Nσ2A(n)≤1069693154N for N≥7.628 517 798×1027, which improves earlier results of the author [‘A note on a result of Ruzsa’, Bull. Aust. Math. Soc.77 (2008), 91–98].