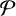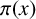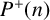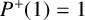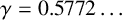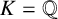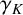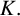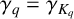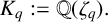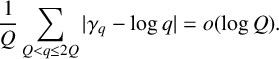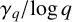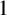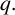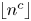Refine search
Actions for selected content:
4 results
ON A CONJECTURE ON SHIFTED PRIMES WITH LARGE PRIME FACTORS, II
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 111 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 13 September 2024, pp. 48-55
- Print publication:
- February 2025
-
- Article
- Export citation
EULER–KRONECKER CONSTANTS FOR CYCLOTOMIC FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 107 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 30 May 2022, pp. 79-84
- Print publication:
- February 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
4 - The Breakthrough of Goldston, Motohashi, Pintz and Yildirim
-
- Book:
- Bounded Gaps Between Primes
- Published online:
- 10 September 2021
- Print publication:
- 25 February 2021, pp 114-183
-
- Chapter
- Export citation
The level of distribution of the Thue–Morse sequence
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 12 / December 2020
- Published online by Cambridge University Press:
- 25 January 2021, pp. 2560-2587
- Print publication:
- December 2020
-
- Article
- Export citation