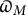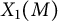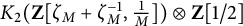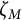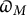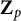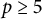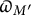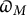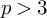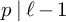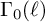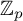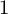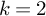Refine search
Actions for selected content:
2 results
Level compatibility in Sharifi’s conjecture
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 11 April 2023, pp. 1194-1212
- Print publication:
- December 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THE EISENSTEIN IDEAL OF WEIGHT k AND RANKS OF HECKE ALGEBRAS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 2 / March 2024
- Published online by Cambridge University Press:
- 31 March 2023, pp. 983-1017
- Print publication:
- March 2024
-
- Article
- Export citation