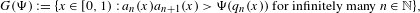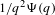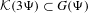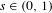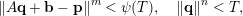Refine search
Actions for selected content:
5 results
METRICAL PROPERTIES OF CONTINUED FRACTION AND LÜROTH SERIES EXPANSIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 112 / Issue 3 / December 2025
- Published online by Cambridge University Press:
- 04 September 2025, pp. 563-567
- Print publication:
- December 2025
-
- Article
-
- You have access
- HTML
- Export citation
METRICAL PROBLEMS IN DIOPHANTINE APPROXIMATION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 3 / December 2021
- Published online by Cambridge University Press:
- 26 July 2021, pp. 519-521
- Print publication:
- December 2021
-
- Article
-
- You have access
- HTML
- Export citation
4 - L-functions from number theory
-
- Book:
- Zeta and L-Functions of Varieties and Motives
- Published online:
- 28 April 2020
- Print publication:
- 07 May 2020, pp 73-103
-
- Chapter
- Export citation
The sets of Dirichlet non-improvable numbers versus well-approximable numbers
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 12 / December 2020
- Published online by Cambridge University Press:
- 27 June 2019, pp. 3217-3235
- Print publication:
- December 2020
-
- Article
- Export citation
An inhomogeneous Dirichlet theorem via shrinking targets
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 7 / July 2019
- Published online by Cambridge University Press:
- 25 June 2019, pp. 1402-1423
- Print publication:
- July 2019
-
- Article
- Export citation