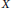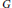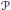Refine search
Actions for selected content:
1 results
A Note on Fine Graphs and Homological Isoperimetric Inequalities
-
- Journal:
- Canadian Mathematical Bulletin / Volume 59 / Issue 1 / 01 March 2016
- Published online by Cambridge University Press:
- 20 November 2018, pp. 170-181
- Print publication:
- 01 March 2016
-
- Article
-
- You have access
- Export citation