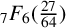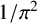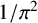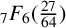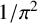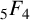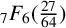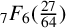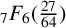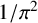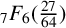Refine search
Actions for selected content:
6 results
1 - Introduction
-
- Book:
- Markov Chains with Asymptotically Zero Drift
- Published online:
- 24 April 2025
- Print publication:
- 08 May 2025, pp 1-40
-
- Chapter
- Export citation
ON GUILLERA’S
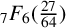 ${}_{7}F_{6}( \frac {27}{64} )$-SERIES FOR
${}_{7}F_{6}( \frac {27}{64} )$-SERIES FOR 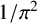 ${1}/{\pi ^2}$
${1}/{\pi ^2}$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 3 / December 2023
- Published online by Cambridge University Press:
- 09 February 2023, pp. 464-471
- Print publication:
- December 2023
-
- Article
- Export citation
Chapter 1 - Poetry
- from Part I - Genre and Medium
-
-
- Book:
- A History of American Literature and Culture of the First World War
- Published online:
- 23 January 2021
- Print publication:
- 04 February 2021, pp 23-38
-
- Chapter
- Export citation
AGGREGATION AND CAPITAL ALLOCATION FORMULAS FOR BIVARIATE DISTRIBUTIONS
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 32 / Issue 4 / October 2018
- Published online by Cambridge University Press:
- 25 September 2017, pp. 556-566
-
- Article
- Export citation
Design of Frame-Like Periodic Solids for Isotropic Symmetry by Member Sizing
-
- Journal:
- Journal of Mechanics / Volume 33 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 11 July 2016, pp. 41-54
- Print publication:
- February 2017
-
- Article
- Export citation
A CLOSED-FORM SOLUTION TO A MODEL OF TWO-SIDED, PARTIAL ALTRUISM
-
- Journal:
- Macroeconomic Dynamics / Volume 16 / Issue 2 / April 2012
- Published online by Cambridge University Press:
- 26 March 2012, pp. 230-239
-
- Article
- Export citation