No CrossRef data available.
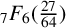 ${}_{7}F_{6}( \frac {27}{64} )$-SERIES FOR
${}_{7}F_{6}( \frac {27}{64} )$-SERIES FOR 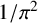 ${1}/{\pi ^2}$
${1}/{\pi ^2}$Published online by Cambridge University Press: 09 February 2023
In 2011, Guillera [‘A new Ramanujan-like series for 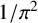 $1/\pi ^2$’, Ramanujan J. 26 (2011), 369–374] introduced a remarkable rational
$1/\pi ^2$’, Ramanujan J. 26 (2011), 369–374] introduced a remarkable rational 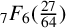 ${}_{7}F_{6}( \frac {27}{64} )$-series for
${}_{7}F_{6}( \frac {27}{64} )$-series for 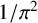 ${1}/{\pi ^2}$ using the Wilf–Zeilberger (WZ) method, and Chu and Zhang later proved this evaluation using an acceleration method based on Dougall’s
${1}/{\pi ^2}$ using the Wilf–Zeilberger (WZ) method, and Chu and Zhang later proved this evaluation using an acceleration method based on Dougall’s 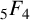 ${}_{5}F_{4}$-sum. Another proof of Guillera’s
${}_{5}F_{4}$-sum. Another proof of Guillera’s 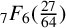 ${}_{7}F_{6}( \frac {27}{64} )$-series was given by Guillera in 2018, and this subsequent proof used a recursive argument involving Dougall’s sum together with the WZ method. Subsequently, Chen and Chu introduced a q-analogue of Guillera’s
${}_{7}F_{6}( \frac {27}{64} )$-series was given by Guillera in 2018, and this subsequent proof used a recursive argument involving Dougall’s sum together with the WZ method. Subsequently, Chen and Chu introduced a q-analogue of Guillera’s  ${}_{7}F_{6}( \frac {27}{64} )$-series. The many past research articles concerning Guillera’s
${}_{7}F_{6}( \frac {27}{64} )$-series. The many past research articles concerning Guillera’s  ${}_{7}F_{6}( \frac {27}{64} )$-series for
${}_{7}F_{6}( \frac {27}{64} )$-series for 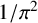 ${1}/{\pi ^2}$ naturally lead to questions about similar results for other mathematical constants. We apply a WZ-based acceleration method to prove new rational
${1}/{\pi ^2}$ naturally lead to questions about similar results for other mathematical constants. We apply a WZ-based acceleration method to prove new rational 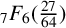 ${}_{7}F_{6}( \frac {27}{64} )$- and
${}_{7}F_{6}( \frac {27}{64} )$- and 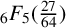 ${}_{6}F_{5}( \frac {27}{64} )$-series for
${}_{6}F_{5}( \frac {27}{64} )$-series for 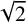 $\sqrt {2}$.
$\sqrt {2}$.