Refine search
Actions for selected content:
1 results
Generalized Morrey Regularity for Parabolic Equations with Discontinuous Data
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 58 / Issue 1 / February 2015
- Published online by Cambridge University Press:
- 10 December 2014, pp. 199-218
-
- Article
-
- You have access
- Export citation
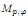 of sublinear operators generated by the parabolic Calderón—Zygmund operator and by the commutator of this operator with bounded mean oscillation (BMO) functions. As a consequence, we obtain a global
of sublinear operators generated by the parabolic Calderón—Zygmund operator and by the commutator of this operator with bounded mean oscillation (BMO) functions. As a consequence, we obtain a global 