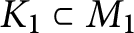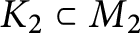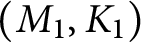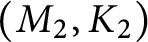Refine search
Actions for selected content:
2 results
A splicing formula for the LMO invariant
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 6 / December 2021
- Published online by Cambridge University Press:
- 20 August 2020, pp. 1743-1770
- Print publication:
- December 2021
-
- Article
- Export citation
Application of Braiding Sequences. II. Polynomial Invariants of Positive Knots
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 59 / Issue 4 / November 2016
- Published online by Cambridge University Press:
- 03 March 2016, pp. 1037-1064
-
- Article
- Export citation