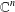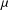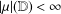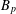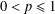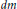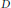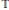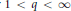Weighted composition operators on weighted Bergman and Dirichlet spaces
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 28 April 2022, pp. 286-302
- Print publication:
- March 2023
-
- Article
- Export citation
\unicode[STIX]{x1D6F7}-CARLESON MEASURES AND MULTIPLIERS BETWEEN BERGMAN–ORLICZ SPACES OF THE UNIT BALL OF \mathbb{C}^{n}
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 104 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 22 March 2017, pp. 63-79
- Print publication:
- February 2018
-
- Article
-
- You have access
- Export citation
AN INTEGRAL REPRESENTATION FOR BESOV AND LIPSCHITZ SPACES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 98 / Issue 1 / February 2015
- Published online by Cambridge University Press:
- 17 October 2014, pp. 129-144
- Print publication:
- February 2015
-
- Article
-
- You have access
- Export citation
BMO Functions and Carleson Measures with Values in Uniformly Convex Spaces
-
- Journal:
- Canadian Journal of Mathematics / Volume 62 / Issue 4 / 01 August 2010
- Published online by Cambridge University Press:
- 20 November 2018, pp. 827-844
- Print publication:
- 01 August 2010
-
- Article
-
- You have access
- Export citation
Rearrangements of the Haar system that preserve BMO
-
- Journal:
- Proceedings of the London Mathematical Society / Volume 75 / Issue 3 / November 1997
- Published online by Cambridge University Press:
- 01 November 1997, pp. 600-618
- Print publication:
- November 1997
-
- Article
- Export citation