We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
Let 
$\mathcal {R}f$ be the randomization of an analytic function over the unit disk in the complex plane where 
$$ \begin{align*}\mathcal{R} f(z) =\sum_{n=0}^\infty a_n X_n z^n \in H({\mathbb D}), \end{align*} $$
$f(z)=\sum _{n=0}^\infty a_n z^n \in H({\mathbb D})$ and 
$(X_n)_{n \geq 0}$ is a standard sequence of independent Bernoulli, Steinhaus, or complex Gaussian random variables. In this paper, we demonstrate that prescribing a polynomial growth rate for random analytic functions over the unit disk leads to rather satisfactory characterizations of those 
$f \in H({\mathbb D})$ such that 
${\mathcal R} f$ admits a given rate almost surely. In particular, we show that the growth rate of the random functions, the growth rate of their Taylor coefficients, and the asymptotic distribution of their zero sets can mutually, completely determine each other. Although the problem is purely complex analytic, the key strategy in the proofs is to introduce a class of auxiliary Banach spaces, which facilitate quantitative estimates.
Let 
$f(z)=\sum _{n=0}^{\infty }a_n z^n \in H(\mathbb {D})$ be an analytic function over the unit disk in the complex plane, and let 
$\mathcal {R} f$ be its randomization: 
$$ \begin{align*}(\mathcal{R} f)(z)= \sum_{n=0}^{\infty} a_n X_n z^n \in H(\mathbb{D}),\end{align*} $$
where 
$(X_n)_{n\ge 0}$ is a standard sequence of independent Bernoulli, Steinhaus, or Gaussian random variables. In this note, we characterize those 
$f(z) \in H(\mathbb {D})$ such that the zero set of 
$\mathcal {R} f$ satisfies a Blaschke-type condition almost surely: 
$$ \begin{align*}\sum_{n=1}^{\infty}(1-|z_n|)^t<\infty, \quad t>1.\end{align*} $$
For n≥2, a hypersurface in the open unit ball Bn in 
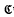is constructed which satisfies the generalized Blaschke condition and is a uniqueness set for all Hp(Bn) with p>0. If n≥3, the hypersurface can be chosen to have finite area.
Subject classification (Amer. Math. Soc. (MOS) 1970): primary 32 A 10.
