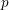Refine search
Actions for selected content:
7 results
SPECIAL VALUES OF THE ZETA FUNCTION OF AN ARITHMETIC SURFACE
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 6 / November 2022
- Published online by Cambridge University Press:
- 15 March 2021, pp. 2043-2091
- Print publication:
- November 2022
-
- Article
-
- You have access
- Open access
- Export citation
The
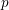 $p$ -adic Gross–Zagier formula on Shimura curves
$p$ -adic Gross–Zagier formula on Shimura curves
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 10 / October 2017
- Published online by Cambridge University Press:
- 11 July 2017, pp. 1987-2074
- Print publication:
- October 2017
-
- Article
- Export citation
Parity conjectures for elliptic curves over global fields of positive characteristic
- Part of
-
- Journal:
- Compositio Mathematica / Volume 147 / Issue 4 / July 2011
- Published online by Cambridge University Press:
- 04 May 2011, pp. 1105-1128
- Print publication:
- July 2011
-
- Article
-
- You have access
- Export citation
Global divisibility of Heegner points and Tamagawa numbers
- Part of
-
- Journal:
- Compositio Mathematica / Volume 144 / Issue 4 / July 2008
- Published online by Cambridge University Press:
- 01 July 2008, pp. 811-826
- Print publication:
- July 2008
-
- Article
-
- You have access
- Export citation
On Rubin’s variant of the p-adic Birch and Swinnerton-Dyer conjecture
- Part of
-
- Journal:
- Compositio Mathematica / Volume 143 / Issue 6 / November 2007
- Published online by Cambridge University Press:
- 01 November 2007, pp. 1374-1398
- Print publication:
- November 2007
-
- Article
-
- You have access
- Export citation
One- and two-level densities for rational families of elliptic curves: evidence for the underlying group symmetries
-
- Journal:
- Compositio Mathematica / Volume 140 / Issue 4 / July 2004
- Published online by Cambridge University Press:
- 04 December 2007, pp. 952-992
- Print publication:
- July 2004
-
- Article
-
- You have access
- Export citation
On Mordell‘s Equation
-
- Journal:
- Compositio Mathematica / Volume 110 / Issue 3 / February 1998
- Published online by Cambridge University Press:
- 04 December 2007, pp. 335-367
- Print publication:
- February 1998
-
- Article
-
- You have access
- Export citation