We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
An ergodic dynamical system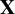 
$\mathbf {X}$ is called dominant if it is isomorphic to a generic extension of itself. It was shown by Glasner et al [On some generic classes of ergodic measure preserving transformations. Trans. Moscow Math. Soc. 82(1) (2021), 15–36] that Bernoulli systems with finite entropy are dominant. In this work, we show first that every ergodic system with positive entropy is dominant, and then that if 
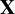$\mathbf {X}$ has zero entropy, then it is not dominant.
