Refine search
Actions for selected content:
3 results
The Determinacy of Context-Free Games
-
- Journal:
- The Journal of Symbolic Logic / Volume 78 / Issue 4 / December 2013
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1115-1134
- Print publication:
- December 2013
-
- Article
- Export citation
Some problems in automata theory which depend on the models of set theory
-
- Journal:
- RAIRO - Theoretical Informatics and Applications / Volume 45 / Issue 4 / November 2011
- Published online by Cambridge University Press:
- 03 October 2011, pp. 383-397
- Print publication:
- November 2011
-
- Article
- Export citation
Unambiguous recognizable two-dimensional languages
-
- Journal:
- RAIRO - Theoretical Informatics and Applications / Volume 40 / Issue 2 / April 2006
- Published online by Cambridge University Press:
- 20 July 2006, pp. 277-293
- Print publication:
- April 2006
-
- Article
- Export citation
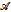 and a Büchi automaton
and a Büchi automaton  such that: (1) There exists a model of ZFC in which Player 2 has a winning strategy in the Wadge game
such that: (1) There exists a model of ZFC in which Player 2 has a winning strategy in the Wadge game