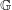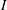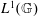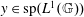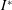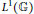Refine search
Actions for selected content:
4 results
Ideals of the Quantum Group Algebra, Arens Regularity and Weakly Compact Multipliers
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 30 January 2020, pp. 825-836
- Print publication:
- December 2020
-
- Article
-
- You have access
- Export citation
ARENS PRODUCTS, ARENS REGULARITY AND RELATED PROBLEMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 1 / August 2020
- Published online by Cambridge University Press:
- 04 December 2019, pp. 138-150
- Print publication:
- August 2020
-
- Article
-
- You have access
- Export citation
A Homological Property and Arens Regularity of Locally Compact Quantum Groups
-
- Journal:
- Canadian Mathematical Bulletin / Volume 60 / Issue 1 / 01 March 2017
- Published online by Cambridge University Press:
- 20 November 2018, pp. 122-130
- Print publication:
- 01 March 2017
-
- Article
-
- You have access
- Export citation
ARENS REGULARITY AND AMENABILITY OF LAU PRODUCT OF BANACH ALGEBRAS DEFINED BY A BANACH ALGEBRA MORPHISM
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 87 / Issue 2 / April 2013
- Published online by Cambridge University Press:
- 31 July 2012, pp. 195-206
- Print publication:
- April 2013
-
- Article
-
- You have access
- Export citation