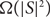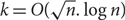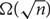Refine search
Actions for selected content:
57 results
Keller–Segel type approximation for nonlocal Fokker–Planck equations in one-dimensional bounded domain
- Part of
-
- Journal:
- European Journal of Applied Mathematics , First View
- Published online by Cambridge University Press:
- 01 August 2025, pp. 1-37
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Coupling results and Markovian structures for number representations of continuous random variables
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 62 / Issue 4 / December 2025
- Published online by Cambridge University Press:
- 28 April 2025, pp. 1340-1359
- Print publication:
- December 2025
-
- Article
- Export citation
On the smoothness of slowly varying functions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 3 / August 2024
- Published online by Cambridge University Press:
- 16 May 2024, pp. 876-891
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
APPROXIMATION OF IRRATIONAL NUMBERS BY PAIRS OF INTEGERS FROM A LARGE SET
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 3 / December 2024
- Published online by Cambridge University Press:
- 03 April 2024, pp. 439-447
- Print publication:
- December 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Approximation and homotopy in regulous geometry
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 09 November 2023, pp. 1-20
- Print publication:
- January 2024
-
- Article
- Export citation
Chapter 20 - An Introduction to Psychologically Plausible Sampling Schemes for Approximating Bayesian Inference
- from Part VI - Computational Approaches
-
-
- Book:
- Sampling in Judgment and Decision Making
- Published online:
- 01 June 2023
- Print publication:
- 15 June 2023, pp 467-489
-
- Chapter
- Export citation
Chapter 21 - Approximating Bayesian Inference through Internal Sampling
- from Part VI - Computational Approaches
-
-
- Book:
- Sampling in Judgment and Decision Making
- Published online:
- 01 June 2023
- Print publication:
- 15 June 2023, pp 490-512
-
- Chapter
- Export citation
9 - Inexactness in Economic Theory
- from Part II - Theory Assessment
-
- Book:
- The Inexact and Separate Science of Economics
- Published online:
- 25 May 2023
- Print publication:
- 08 June 2023, pp 231-255
-
- Chapter
- Export citation

Idealizations in Physics
-
- Published online:
- 11 January 2023
- Print publication:
- 26 January 2023
-
- Element
- Export citation
3 - Expressivity of Deep Neural Networks
-
-
- Book:
- Mathematical Aspects of Deep Learning
- Published online:
- 29 November 2022
- Print publication:
- 22 December 2022, pp 149-199
-
- Chapter
- Export citation
12 - Infinite Orbits and Quitting Games
-
- Book:
- A Course in Stochastic Game Theory
- Published online:
- 05 May 2022
- Print publication:
- 26 May 2022, pp 211-235
-
- Chapter
- Export citation
Large very dense subgraphs in a stream of edges
-
- Journal:
- Network Science / Volume 9 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 25 January 2022, pp. 403-424
-
- Article
- Export citation
3 - Interpersonal Function and Intersubjectivity
-
- Book:
- General Extenders
- Published online:
- 20 August 2021
- Print publication:
- 02 September 2021, pp 43-59
-
- Chapter
- Export citation
11 - Multiperiod Blending
- from Part III - Advanced Methods
-
- Book:
- Chemical Production Scheduling
- Published online:
- 01 May 2021
- Print publication:
- 06 May 2021, pp 261-286
-
- Chapter
- Export citation
APPROXIMATION OF AND BY COMPLETELY MONOTONE FUNCTIONS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 61 / Issue 4 / October 2019
- Published online by Cambridge University Press:
- 06 March 2020, pp. 416-430
-
- Article
-
- You have access
- Export citation
Interaction of Poisson hyperplane processes and convex bodies
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 56 / Issue 4 / December 2019
- Published online by Cambridge University Press:
- 11 December 2019, pp. 1020-1032
- Print publication:
- December 2019
-
- Article
- Export citation
Chapter 5 - Meaning-Shift Units in L2 Learning and Use: Usage vs. Exposure
-
- Book:
- Phraseology and the Advanced Language Learner
- Published online:
- 18 November 2019
- Print publication:
- 28 November 2019, pp 101-152
-
- Chapter
- Export citation
Chapter 7 - Towards the Bigger Picture
-
- Book:
- Phraseology and the Advanced Language Learner
- Published online:
- 18 November 2019
- Print publication:
- 28 November 2019, pp 206-219
-
- Chapter
- Export citation
Chapter 3 - L2 Use and Processing of Multi-Word Units
-
- Book:
- Phraseology and the Advanced Language Learner
- Published online:
- 18 November 2019
- Print publication:
- 28 November 2019, pp 38-65
-
- Chapter
- Export citation
The Korteweg–de Vries, Burgers and Whitham limits for a spatially periodic Boussinesq model
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 30 August 2018, pp. 191-217
- Print publication:
- February 2019
-
- Article
- Export citation