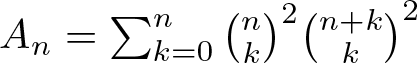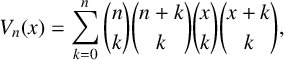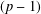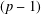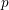Refine search
Actions for selected content:
5 results
On the binomial transforms of Apéry-like sequences
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 08 January 2025, pp. 359-376
- Print publication:
- June 2025
-
- Article
- Export citation
Proof of some conjectural congruences involving Apéry and Apéry-like numbers
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 2 / May 2024
- Published online by Cambridge University Press:
- 07 March 2024, pp. 508-527
-
- Article
- Export citation
ON THE DIVISIBILITY OF SUMS INVOLVING APÉRY-LIKE POLYNOMIALS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 2 / October 2022
- Published online by Cambridge University Press:
- 14 March 2022, pp. 203-208
- Print publication:
- October 2022
-
- Article
- Export citation
CONGRUENCES FOR THE
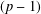 $(p-1)$TH APÉRY NUMBER
$(p-1)$TH APÉRY NUMBER
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 99 / Issue 3 / June 2019
- Published online by Cambridge University Press:
- 28 November 2018, pp. 362-368
- Print publication:
- June 2019
-
- Article
-
- You have access
- Export citation
Arithmetic properties of Apéry-like numbers
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 2 / February 2018
- Published online by Cambridge University Press:
- 20 October 2017, pp. 249-274
- Print publication:
- February 2018
-
- Article
- Export citation