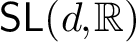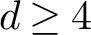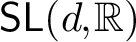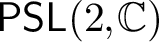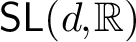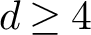Refine search
Actions for selected content:
2 results
A report on an ergodic dichotomy
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 27 February 2023, pp. 236-289
- Print publication:
- January 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
QUASI-ISOMETRIC EMBEDDINGS INAPPROXIMABLE BY ANOSOV REPRESENTATIONS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 5 / September 2023
- Published online by Cambridge University Press:
- 14 March 2022, pp. 2497-2514
- Print publication:
- September 2023
-
- Article
- Export citation