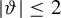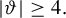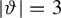1 Introduction
Let
![]() ${\mathsf {G}}$
be the real points of a semi-simple real-algebraic group of the non-compact type. The (Riemannian) globally symmetric space
${\mathsf {G}}$
be the real points of a semi-simple real-algebraic group of the non-compact type. The (Riemannian) globally symmetric space
![]() ${\mathsf {X}}$
associated to
${\mathsf {X}}$
associated to
![]() ${\mathsf {G}}$
is non-positively curved, its visual boundary
${\mathsf {G}}$
is non-positively curved, its visual boundary
![]() $\partial _\infty {\mathsf {X}}$
is a union of compact
$\partial _\infty {\mathsf {X}}$
is a union of compact
![]() ${\mathsf {G}}$
-orbits, parameterized by directions in a (fixed beforehand) closed Weyl chamber
${\mathsf {G}}$
-orbits, parameterized by directions in a (fixed beforehand) closed Weyl chamber
![]() ${\mathfrak a}^+$
of
${\mathfrak a}^+$
of
![]() ${\mathfrak g}.$
The
${\mathfrak g}.$
The
![]() ${\mathsf {G}}$
-orbit associated to a direction
${\mathsf {G}}$
-orbit associated to a direction
![]() ${\mathsf {u}}\in \mathbb {P}({\mathfrak a}^+)$
is
${\mathsf {u}}\in \mathbb {P}({\mathfrak a}^+)$
is
![]() ${\mathsf {G}}$
-equivariantly identified with the flag space
${\mathsf {G}}$
-equivariantly identified with the flag space
![]() $\mathcal {F}_{\vartheta _{\mathsf {u}}}$
of
$\mathcal {F}_{\vartheta _{\mathsf {u}}}$
of
![]() ${\mathsf {G}},$
where
${\mathsf {G}},$
where
![]() $\vartheta _{\mathsf {u}}$
is the subset of simple roots that do not vanish on
$\vartheta _{\mathsf {u}}$
is the subset of simple roots that do not vanish on
![]() ${\mathsf {u}}.$
${\mathsf {u}}.$
Let now
![]() be a finitely generated group and
be a finitely generated group and
![]() a representation with discrete image. A fundamental object of study is the limit set
a representation with discrete image. A fundamental object of study is the limit set
![]() $\mathrm {L}_{\rho }$
of
$\mathrm {L}_{\rho }$
of
![]() on the visual boundary
on the visual boundary
![]() $\partial _\infty {\mathsf {X}},$
defined as the set of accumulation points of an (any) orbit
$\partial _\infty {\mathsf {X}},$
defined as the set of accumulation points of an (any) orbit
![]() on the natural compactification
on the natural compactification
![]() ${\mathsf {X}}\cup \partial _\infty {\mathsf {X}}.$
${\mathsf {X}}\cup \partial _\infty {\mathsf {X}}.$
When
![]() is Zariski-dense, this object has the following topological description by Benoist [Reference Benoist7]: the action of
is Zariski-dense, this object has the following topological description by Benoist [Reference Benoist7]: the action of
![]() on each flag space
on each flag space
![]() $\mathcal F_\vartheta $
has a smallest closed invariant set, called the limit set on
$\mathcal F_\vartheta $
has a smallest closed invariant set, called the limit set on
![]() $\mathcal F_\vartheta $
and denoted by
$\mathcal F_\vartheta $
and denoted by
![]() $\mathrm {L}_\rho ^\vartheta $
; additionally, one has the limit cone
$\mathrm {L}_\rho ^\vartheta $
; additionally, one has the limit cone
![]() $\mathscr L_\rho \subset {\mathfrak a}^+$
of
$\mathscr L_\rho \subset {\mathfrak a}^+$
of
![]() defined as the subset of
defined as the subset of
![]() ${\mathfrak a}^+$
of accumulation points of sequences of the form
${\mathfrak a}^+$
of accumulation points of sequences of the form
where
![]() $t_n\in \mathbb {R}_+$
converges to
$t_n\in \mathbb {R}_+$
converges to
![]() goes to infinity, and
goes to infinity, and
![]() $a:{\mathsf {G}}\to {\mathfrak a}^+$
is the Cartan projection. It is a convex cone with non-empty interior and the limit set
$a:{\mathsf {G}}\to {\mathfrak a}^+$
is the Cartan projection. It is a convex cone with non-empty interior and the limit set
![]() on
on
![]() $\partial _\infty {\mathsf {X}}$
is the ‘fibration’ over
$\partial _\infty {\mathsf {X}}$
is the ‘fibration’ over
![]() $\mathbb {P}(\mathscr L_\rho ),$
whose fiber over a given direction
$\mathbb {P}(\mathscr L_\rho ),$
whose fiber over a given direction
![]() ${\mathsf {u}}\in \mathbb {P}(\mathscr L_\rho )$
is the limit set
${\mathsf {u}}\in \mathbb {P}(\mathscr L_\rho )$
is the limit set
![]() $\mathrm {L}_\rho ^{\vartheta _{\mathsf {u}}}$
of
$\mathrm {L}_\rho ^{\vartheta _{\mathsf {u}}}$
of
![]() on
on
![]() $\mathcal F_{\vartheta _{\mathsf {u}}}.$
$\mathcal F_{\vartheta _{\mathsf {u}}}.$
Inspired by Sullivan’s [Reference Sullivan68] work on the rank-1 case, one may seek to distinguish the subset of conical points of
![]() $\mathrm {L}_\rho $
, that is, points on the limit set that are approached in a uniform manner by elements of the orbit
$\mathrm {L}_\rho $
, that is, points on the limit set that are approached in a uniform manner by elements of the orbit
![]() However, the definition of uniform depends on:
However, the definition of uniform depends on:
-
• the type of
 ${\mathsf {G}}$
-orbit the point lies in—a point
${\mathsf {G}}$
-orbit the point lies in—a point
 $x\in \mathrm {L}_\rho ^\vartheta $
is conical if there exists a (to be called conical) sequence
$x\in \mathrm {L}_\rho ^\vartheta $
is conical if there exists a (to be called conical) sequence
 converging to x such that for every
converging to x such that for every
 $y\in \mathrm {L}^{\operatorname {\mathrm {i}}\vartheta }_\rho $
(here we let
$y\in \mathrm {L}^{\operatorname {\mathrm {i}}\vartheta }_\rho $
(here we let
 $\operatorname {\mathrm {i}}:{\mathfrak a}\to {\mathfrak a}$
be the opposition involution and
$\operatorname {\mathrm {i}}:{\mathfrak a}\to {\mathfrak a}$
be the opposition involution and
 $\operatorname {\mathrm {i}}\vartheta :=\vartheta \circ \operatorname {\mathrm {i}}$
) in general position with x, the sequence
$\operatorname {\mathrm {i}}\vartheta :=\vartheta \circ \operatorname {\mathrm {i}}$
) in general position with x, the sequence
 $\gamma _n^{-1}(y,x)$
has compact closure on the space of pairs of flags in general position
$\gamma _n^{-1}(y,x)$
has compact closure on the space of pairs of flags in general position
 $\mathcal F_\vartheta ^{\kern2pt(2)};$
$\mathcal F_\vartheta ^{\kern2pt(2)};$
-
• the specific direction
 ${\mathsf {u}}\in \mathbb {P}(\mathscr L_\rho ),$
associated to the given point—fix a norm
${\mathsf {u}}\in \mathbb {P}(\mathscr L_\rho ),$
associated to the given point—fix a norm
 $\|\,\|$
on
$\|\,\|$
on
 ${\mathfrak a}$
and define the tube of size
${\mathfrak a}$
and define the tube of size
 $r>0$
as the r-tubular neighborhood then
$r>0$
as the r-tubular neighborhood then $$ \begin{align*}{\mathbb T}_r({\mathsf{u}})=\{v\in{\mathfrak a}:B(v,r)\cap{\mathsf{u}}\neq\emptyset\},\end{align*} $$
$$ \begin{align*}{\mathbb T}_r({\mathsf{u}})=\{v\in{\mathfrak a}:B(v,r)\cap{\mathsf{u}}\neq\emptyset\},\end{align*} $$
 $x\in \mathrm {L}^{\vartheta _{\mathsf {u}}}_\rho $
is
$x\in \mathrm {L}^{\vartheta _{\mathsf {u}}}_\rho $
is
 ${\mathsf {u}}$
-conical if there exists
${\mathsf {u}}$
-conical if there exists
 $r>0$
and a conical sequence
$r>0$
and a conical sequence
 $\gamma _n\to x$
such that for all n, one has
$\gamma _n\to x$
such that for all n, one has  $$ \begin{align*}a(\rho(\gamma_n))\in{\mathbb T}_r({\mathsf{u}}).\end{align*} $$
$$ \begin{align*}a(\rho(\gamma_n))\in{\mathbb T}_r({\mathsf{u}}).\end{align*} $$
A measurable description has been recently established by Burger et al [Reference Burger, Landesberg, Lee and Oh20] for
![]() ${\mathsf {u}}$
-conical points of Zariski-dense subgroups: under some extra assumptions, the Patterson–Sullivan measure associated to the direction
${\mathsf {u}}$
-conical points of Zariski-dense subgroups: under some extra assumptions, the Patterson–Sullivan measure associated to the direction
![]() ${\mathsf {u}}$
charges totally the subset of
${\mathsf {u}}$
charges totally the subset of
![]() ${\mathsf {u}}$
-conical points if and only if
${\mathsf {u}}$
-conical points if and only if
![]() ${\mathsf {G}}$
has rank
${\mathsf {G}}$
has rank
![]() $\leq 3;$
if
$\leq 3;$
if
![]() $\operatorname {\mathrm {rank}}{\mathsf {G}}\geq 4$
, then the subset of
$\operatorname {\mathrm {rank}}{\mathsf {G}}\geq 4$
, then the subset of
![]() ${\mathsf {u}}$
-conical points has zero mass.
${\mathsf {u}}$
-conical points has zero mass.
In this paper, we will also study a measurable description of
![]() ${\mathsf {u}}$
-conical limit points, but for general Anosov representations, a class introduced by Labourie [Reference Labourie43] for fundamental groups of closed negatively curved manifolds and generalized by Guichard and Wienhard [Reference Guichard and Wienhard35] for arbitrary (finitely generated) word-hyperbolic groups. Thanks to the recent work by Kapovich, Leeb, and Porti [Reference Kapovich, Leeb and Porti40] (see also those of Bochi, Potrie, and Sambarino [Reference Bochi, Potrie and Sambarino10] and Guéritaud et al [Reference Guéritaud, Guichard, Kassel and Wienhard34]), we can define them as follows, see §5.2.
${\mathsf {u}}$
-conical limit points, but for general Anosov representations, a class introduced by Labourie [Reference Labourie43] for fundamental groups of closed negatively curved manifolds and generalized by Guichard and Wienhard [Reference Guichard and Wienhard35] for arbitrary (finitely generated) word-hyperbolic groups. Thanks to the recent work by Kapovich, Leeb, and Porti [Reference Kapovich, Leeb and Porti40] (see also those of Bochi, Potrie, and Sambarino [Reference Bochi, Potrie and Sambarino10] and Guéritaud et al [Reference Guéritaud, Guichard, Kassel and Wienhard34]), we can define them as follows, see §5.2.
Definition 1.0.1. Let
![]() $\vartheta \subset {{\Delta }}$
be a non-empty subset of simple roots and denote by
$\vartheta \subset {{\Delta }}$
be a non-empty subset of simple roots and denote by
![]() $|\,|$
the word length on
$|\,|$
the word length on
![]() for some (fixed) symmetric generating set. A representation
for some (fixed) symmetric generating set. A representation
![]() is
is
![]() $\vartheta $
-Anosov if there exist positive constants
$\vartheta $
-Anosov if there exist positive constants
![]() $c,\mu $
such that for all
$c,\mu $
such that for all
![]() and
and
![]() $\sigma \in \vartheta $
, one has
$\sigma \in \vartheta $
, one has
A key feature of a
![]() $\vartheta $
-Anosov representation
$\vartheta $
-Anosov representation
![]() $\rho $
is that
$\rho $
is that
is necessarily word-hyperbolic and there exist continuous
![]() $\rho $
-equivariant limit maps (Proposition 5.2.3) defined on its Gromov boundary,
$\rho $
-equivariant limit maps (Proposition 5.2.3) defined on its Gromov boundary,

such that the flags
![]() $\xi ^{\operatorname {\mathrm {i}}\vartheta }(x)$
and
$\xi ^{\operatorname {\mathrm {i}}\vartheta }(x)$
and
![]() $\xi ^\vartheta (y)$
are in general position whenever
$\xi ^\vartheta (y)$
are in general position whenever
![]() $x\neq y.$
$x\neq y.$
We begin by studying the Patterson–Sullivan theory for these groups. Fix then
![]() $\vartheta \subset {{{\Delta }}},$
let
$\vartheta \subset {{{\Delta }}},$
let
be the center of the associated Levi group and let
![]() $p_\vartheta :{\mathfrak a}\to {\mathfrak a}_\vartheta $
be the projection invariant under the subgroup of the Weyl group point-wise fixing
$p_\vartheta :{\mathfrak a}\to {\mathfrak a}_\vartheta $
be the projection invariant under the subgroup of the Weyl group point-wise fixing
![]() ${\mathfrak a}_\vartheta $
(see §4.2). The dual space
${\mathfrak a}_\vartheta $
(see §4.2). The dual space
![]() $({\mathfrak a}_\vartheta )^*$
sits naturally as the subspace of
$({\mathfrak a}_\vartheta )^*$
sits naturally as the subspace of
![]() ${\mathfrak a}^*$
of
${\mathfrak a}^*$
of
![]() $p_\vartheta $
-invariant linear forms. It is spanned by the fundamental weights of the elements in
$p_\vartheta $
-invariant linear forms. It is spanned by the fundamental weights of the elements in
![]() $\vartheta $
:
$\vartheta $
:
Let us write
![]() $a_\vartheta $
for the composition
$a_\vartheta $
for the composition
![]() $a_\vartheta =p_\vartheta \circ a:{\mathsf {G}}\to {\mathfrak a}_\vartheta .$
$a_\vartheta =p_\vartheta \circ a:{\mathsf {G}}\to {\mathfrak a}_\vartheta .$
Let
![]() $\beta :{\mathsf {G}}\times \mathcal F_{{{\Delta }}}\to {\mathfrak a}$
be the Buseman–Iwasawa cocycle of
$\beta :{\mathsf {G}}\times \mathcal F_{{{\Delta }}}\to {\mathfrak a}$
be the Buseman–Iwasawa cocycle of
![]() ${\mathsf {G}}$
introduced by Quint [Reference Quint62] (see §4.6). The map
${\mathsf {G}}$
introduced by Quint [Reference Quint62] (see §4.6). The map
![]() $\beta _\vartheta =p_\vartheta \circ \beta $
factors as a cocycle
$\beta _\vartheta =p_\vartheta \circ \beta $
factors as a cocycle
![]() $\beta _\vartheta :{\mathsf {G}}\times \mathcal F_\vartheta \to {\mathfrak a}_\vartheta .$
$\beta _\vartheta :{\mathsf {G}}\times \mathcal F_\vartheta \to {\mathfrak a}_\vartheta .$
Definition 1.0.2. A Patterson–Sullivan measure for
![]() $\rho $
on
$\rho $
on
![]() $\mathcal F_\vartheta $
is a probability measure
$\mathcal F_\vartheta $
is a probability measure
![]() $\nu $
on
$\nu $
on
![]() $\mathcal F_\vartheta $
such that there exists
$\mathcal F_\vartheta $
such that there exists
![]() $\varphi \in {\mathfrak a}_\vartheta ^*$
with, for every
$\varphi \in {\mathfrak a}_\vartheta ^*$
with, for every
![]()
For
![]() $\varphi \in ({\mathfrak a}_\vartheta )^*$
, denote
$\varphi \in ({\mathfrak a}_\vartheta )^*$
, denote
and, inspired by Quint’s growth indicator [Reference Quint61], consider the
![]() $\vartheta $
-critical hypersurface
$\vartheta $
-critical hypersurface
Let us define the
![]() $\vartheta $
-limit cone of
$\vartheta $
-limit cone of
![]() $\rho ,$
denoted by
$\rho ,$
denoted by
![]() $\mathscr L_{\vartheta ,\rho },$
as the asymptotic cone of the projections
$\mathscr L_{\vartheta ,\rho },$
as the asymptotic cone of the projections
that is, all limits of sequences of the form
![]() $t_n a_\vartheta (\rho (\gamma _n)),$
where
$t_n a_\vartheta (\rho (\gamma _n)),$
where
![]() $\gamma _n\to \infty $
in
$\gamma _n\to \infty $
in
and
![]() $t_n\to 0$
in
$t_n\to 0$
in
![]() $\mathbb {R}_+.$
$\mathbb {R}_+.$
In the real case, if
![]() is Zariski-dense, then Benoist’s aforementioned result implies that
is Zariski-dense, then Benoist’s aforementioned result implies that
![]() $\mathscr L_{\vartheta ,\rho }$
has non-empty interior. However, for arbitrary local fields, this is no longer the case (even assuming Zariski-density and Anosov). We aim to work on this more general context, so let us assume now that
$\mathscr L_{\vartheta ,\rho }$
has non-empty interior. However, for arbitrary local fields, this is no longer the case (even assuming Zariski-density and Anosov). We aim to work on this more general context, so let us assume now that
![]() ${\mathsf {G}}$
is (the
${\mathsf {G}}$
is (the
![]() $\mathbb {K}$
-points of) a semi-simple algebraic group over a local field
$\mathbb {K}$
-points of) a semi-simple algebraic group over a local field
![]() $\mathbb {K}.$
We refer the reader to §4 for the analogous definitions, where
$\mathbb {K}.$
We refer the reader to §4 for the analogous definitions, where
![]() ${\mathfrak a}_\vartheta $
is replaced by the real vector space
${\mathfrak a}_\vartheta $
is replaced by the real vector space
![]() ${\mathsf {E}}_\vartheta ,$
etc.
${\mathsf {E}}_\vartheta ,$
etc.
Let
![]() $\mathrm {Ann}(\mathscr L_{\vartheta ,\rho })$
be the annihilator of the
$\mathrm {Ann}(\mathscr L_{\vartheta ,\rho })$
be the annihilator of the
![]() $\vartheta $
-limit cone and denote by
$\vartheta $
-limit cone and denote by
![]() $\pi ^\vartheta _\rho :({\mathsf {E}}_\vartheta )^*\to ({\mathsf {E}}_\vartheta )^*/\mathrm {Ann}(\mathscr L_{\vartheta ,\rho })$
the quotient projection.
$\pi ^\vartheta _\rho :({\mathsf {E}}_\vartheta )^*\to ({\mathsf {E}}_\vartheta )^*/\mathrm {Ann}(\mathscr L_{\vartheta ,\rho })$
the quotient projection.
Theorem A. Let
![]() be
be
![]() $\vartheta $
-Anosov. Then,
$\vartheta $
-Anosov. Then,
![]() $\mathcal Q_{\vartheta ,\rho }$
is a closed co-dimension-one analytic sub-manifold of
$\mathcal Q_{\vartheta ,\rho }$
is a closed co-dimension-one analytic sub-manifold of
![]() $({\mathsf {E}}_\vartheta )^*$
that bounds a convex set; moreover, the projection
$({\mathsf {E}}_\vartheta )^*$
that bounds a convex set; moreover, the projection
![]() $\pi ^\vartheta _\rho (\mathcal Q_{\vartheta ,\rho })$
is also a closed co-dimension-one analytic sub-manifold boundary of a strictly convex set. For each
$\pi ^\vartheta _\rho (\mathcal Q_{\vartheta ,\rho })$
is also a closed co-dimension-one analytic sub-manifold boundary of a strictly convex set. For each
![]() $\varphi \in \mathcal Q_{\vartheta ,\rho }$
, there exists a unique Patterson–Sullivan measure
$\varphi \in \mathcal Q_{\vartheta ,\rho }$
, there exists a unique Patterson–Sullivan measure
![]() $\nu ^\varphi $
with support on
$\nu ^\varphi $
with support on
![]() The map
The map
![]() $\varphi \mapsto \nu ^\varphi $
is an analytic homeomorphism between the projection
$\varphi \mapsto \nu ^\varphi $
is an analytic homeomorphism between the projection
![]() $\pi ^\vartheta _\rho (\mathcal Q_{\vartheta ,\rho })$
and the space of Patterson–Sullivan measures on
$\pi ^\vartheta _\rho (\mathcal Q_{\vartheta ,\rho })$
and the space of Patterson–Sullivan measures on
![]() $\mathcal F_\vartheta $
whose support is contained in
$\mathcal F_\vartheta $
whose support is contained in
![]() Such Patterson–Sullivan measures are ergodic and pairwise mutually singular.
Such Patterson–Sullivan measures are ergodic and pairwise mutually singular.
We refer the reader to Corollary 5.5.3 and Proposition 5.9.2 for the proofs of the above statements.
The fact that both
![]() $\mathcal Q_{\vartheta ,\rho }$
and
$\mathcal Q_{\vartheta ,\rho }$
and
![]() $\pi ^\vartheta _\rho (\mathcal Q_{\vartheta ,\rho })$
are closed analytic hypersurfaces is stated by Potrie and Sambarino [Reference Potrie and Sambarino57, Proposition 4.11] for
$\pi ^\vartheta _\rho (\mathcal Q_{\vartheta ,\rho })$
are closed analytic hypersurfaces is stated by Potrie and Sambarino [Reference Potrie and Sambarino57, Proposition 4.11] for
![]() $\mathbb {K}=\mathbb {R}$
with essentially the same arguments. The parameterization of Patterson–Sullivan measures by
$\mathbb {K}=\mathbb {R}$
with essentially the same arguments. The parameterization of Patterson–Sullivan measures by
![]() $\pi ^\vartheta _\rho (\mathcal Q_{\vartheta ,\rho })$
was previously established by Lee and Oh [Reference Lee and Oh46, Theorem 1.3] for
$\pi ^\vartheta _\rho (\mathcal Q_{\vartheta ,\rho })$
was previously established by Lee and Oh [Reference Lee and Oh46, Theorem 1.3] for
![]() $\mathbb {K}=\mathbb {R}, \vartheta ={{{\Delta }}}$
, and assuming Zariski-density of
$\mathbb {K}=\mathbb {R}, \vartheta ={{{\Delta }}}$
, and assuming Zariski-density of
![]() Existence and ergodicity was previously established, for
Existence and ergodicity was previously established, for
![]() $\mathbb {K}=\mathbb {R}$
, by Dey and Kapovich [Reference Dey and Kapovich29, Main Theorem] for
$\mathbb {K}=\mathbb {R}$
, by Dey and Kapovich [Reference Dey and Kapovich29, Main Theorem] for
![]() $\operatorname {\mathrm {i}}$
-invariant functionals
$\operatorname {\mathrm {i}}$
-invariant functionals
![]() $\varphi \in ({\mathfrak a}^+)^*\cap ({\mathfrak a}_\vartheta )^*$
and
$\varphi \in ({\mathfrak a}^+)^*\cap ({\mathfrak a}_\vartheta )^*$
and
![]() $\operatorname {\mathrm {i}}$
-invariant subsets
$\operatorname {\mathrm {i}}$
-invariant subsets
![]() $\vartheta ;$
and by Sambarino [Reference Sambarino66, Corollary 4.22] for arbitrary functionals but Zariski-dense representations of fundamental groups of negatively curved manifolds. Existence of Patterson–Sullivan measures has also been established by Canary, Zhang, and Zimmer [Reference Canary, Zhang and Zimmer21] in the real case for relative Anosov representations.
$\vartheta ;$
and by Sambarino [Reference Sambarino66, Corollary 4.22] for arbitrary functionals but Zariski-dense representations of fundamental groups of negatively curved manifolds. Existence of Patterson–Sullivan measures has also been established by Canary, Zhang, and Zimmer [Reference Canary, Zhang and Zimmer21] in the real case for relative Anosov representations.
We keep the discussion for
![]() $\mathbb {K}=\mathbb {R}$
since this is essential in the following result. Consider
$\mathbb {K}=\mathbb {R}$
since this is essential in the following result. Consider
![]() $\varphi \in \mathcal Q_{\vartheta ,\rho }$
with associated Patterson–Sullivan measure
$\varphi \in \mathcal Q_{\vartheta ,\rho }$
with associated Patterson–Sullivan measure
![]() $\mu ^\varphi .$
Via the duality
$\mu ^\varphi .$
Via the duality
the tangent space
![]() ${\mathsf {T}}_{\varphi }\mathcal Q_{\vartheta ,\rho }$
gives a direction
${\mathsf {T}}_{\varphi }\mathcal Q_{\vartheta ,\rho }$
gives a direction
![]() ${\mathsf {u}}_\varphi $
of
${\mathsf {u}}_\varphi $
of
![]() $\mathbb {P}({\mathfrak a}_\vartheta )$
contained in the relative interior of the limit cone
$\mathbb {P}({\mathfrak a}_\vartheta )$
contained in the relative interior of the limit cone
![]() $\mathscr L_{\vartheta ,\rho }$
(Corollary 5.9.1). We then further investigate the
$\mathscr L_{\vartheta ,\rho }$
(Corollary 5.9.1). We then further investigate the
![]() $\mu ^\varphi $
-mass of
$\mu ^\varphi $
-mass of
![]() ${\mathsf {u}}_\varphi $
-conical points on
${\mathsf {u}}_\varphi $
-conical points on
![]()
Since we are dealing with the limit cone on
![]() ${\mathfrak a}_\vartheta $
(and not on
${\mathfrak a}_\vartheta $
(and not on
![]() ${\mathfrak a}$
as before),
${\mathfrak a}$
as before),
![]() ${\mathsf {u}}_\varphi $
-conical points are yet to be defined. It is standard that every point
${\mathsf {u}}_\varphi $
-conical points are yet to be defined. It is standard that every point
is conical. (This follows from the fact that every point
is conical and the existence of the equivariant limit maps for
![]() $\rho $
). Let us say it is further
$\rho $
). Let us say it is further
![]() ${\mathsf {u}}_\varphi $
-conical if there exists a conical sequence (for x) as above and
${\mathsf {u}}_\varphi $
-conical if there exists a conical sequence (for x) as above and
![]() $r>0$
such that
$r>0$
such that
![]() $a_\vartheta (\rho (\gamma _n))\in {\mathbb T}_r({\mathsf {u}}_\varphi ).$
Denote by
$a_\vartheta (\rho (\gamma _n))\in {\mathbb T}_r({\mathsf {u}}_\varphi ).$
Denote by
the subset
Theorem B. (Theorem 5.13.3)
Let
![]() $\mathbb {K}=\mathbb {R}$
and assume
$\mathbb {K}=\mathbb {R}$
and assume
![]() $\rho $
is
$\rho $
is
![]() $\vartheta $
-Anosov and Zariski-dense. If
$\vartheta $
-Anosov and Zariski-dense. If
![]() $|\vartheta |\leq 2$
, then
$|\vartheta |\leq 2$
, then
![]() if
if
![]() $|\vartheta |\geq 4$
, then
$|\vartheta |\geq 4$
, then
![]()
The case
![]() $|\vartheta |=3$
is sadly presently untreated. The missing fact that would make our technique directly apply is an ergodicity result for translation skew-products over metric-Anosov flows where the abelian group is isomorphic to
$|\vartheta |=3$
is sadly presently untreated. The missing fact that would make our technique directly apply is an ergodicity result for translation skew-products over metric-Anosov flows where the abelian group is isomorphic to
![]() $\mathbb {R}^2=\mathbb {R}^{|\vartheta |-1},$
more precisely, we need equivalence between ergodicity and
$\mathbb {R}^2=\mathbb {R}^{|\vartheta |-1},$
more precisely, we need equivalence between ergodicity and
![]() $\dim V\leq 2$
in Corollary 2.5.5.
$\dim V\leq 2$
in Corollary 2.5.5.
When
![]() $\vartheta ={{{\Delta }}},$
a stronger version of Theorem B dealing also with the case
$\vartheta ={{{\Delta }}},$
a stronger version of Theorem B dealing also with the case
![]() $|{{{\Delta }}}|=3$
was previously established by Burger et al [Reference Burger, Landesberg, Lee and Oh20, Theorem 1.6]. It is likely that the combination of their techniques and ours settles the missing
$|{{{\Delta }}}|=3$
was previously established by Burger et al [Reference Burger, Landesberg, Lee and Oh20, Theorem 1.6]. It is likely that the combination of their techniques and ours settles the missing
![]() $|\vartheta |=3$
case.
$|\vartheta |=3$
case.
1.1 General strategy for Theorem B
Let us briefly explain the proof of Theorem B, which we believe is the main contribution of this work. The main ingredient is a precise description of the
![]() $\vartheta $
-parallel sets dynamics of
$\vartheta $
-parallel sets dynamics of
![]() ${\mathsf {G}}.$
If
${\mathsf {G}}.$
If
![]() $(x,y)\in \mathcal F_{\operatorname {\mathrm {i}}\vartheta }\times \mathcal F_\vartheta $
are in general position, the associated parallel set is a subset of
$(x,y)\in \mathcal F_{\operatorname {\mathrm {i}}\vartheta }\times \mathcal F_\vartheta $
are in general position, the associated parallel set is a subset of
![]() ${\mathsf {X}} $
consisting of the union of totally geodesic maximal flats
${\mathsf {X}} $
consisting of the union of totally geodesic maximal flats
![]() ${\mathsf {p}}$
of
${\mathsf {p}}$
of
![]() ${\mathsf {X}}$
whose associated complete flags in the Furstenberg boundary
${\mathsf {X}}$
whose associated complete flags in the Furstenberg boundary
![]() ${\mathsf {p}}(-{\mathfrak a}^+)$
and
${\mathsf {p}}(-{\mathfrak a}^+)$
and
![]() ${\mathsf {p}}({\mathfrak a}^+)$
contain respectively x and y as a partial flag. This parallel set is a reductive symmetric space and the associated dynamical system consists of moving along its center.
${\mathsf {p}}({\mathfrak a}^+)$
contain respectively x and y as a partial flag. This parallel set is a reductive symmetric space and the associated dynamical system consists of moving along its center.
More concisely, if one considers the space
![]() $\mathcal F^{(2)}_\vartheta \subset \mathcal F_{\operatorname {\mathrm {i}}\vartheta }\times \mathcal F_\vartheta $
of transverse flags, then the space
$\mathcal F^{(2)}_\vartheta \subset \mathcal F_{\operatorname {\mathrm {i}}\vartheta }\times \mathcal F_\vartheta $
of transverse flags, then the space
![]() $\mathcal F^{(2)}_\vartheta \times {\mathfrak a}_\vartheta $
carries a
$\mathcal F^{(2)}_\vartheta \times {\mathfrak a}_\vartheta $
carries a
![]() ${\mathsf {G}}$
-action (on the left) given by
${\mathsf {G}}$
-action (on the left) given by
and an
![]() ${\mathfrak a}_\vartheta $
-action (on the right) by translation on the last coordinate.
${\mathfrak a}_\vartheta $
-action (on the right) by translation on the last coordinate.
Observe however that the left-action of
![]() on
on
![]() $\mathcal F^{(2)}_\vartheta \times {\mathfrak a}_\vartheta $
need not be proper. For
$\mathcal F^{(2)}_\vartheta \times {\mathfrak a}_\vartheta $
need not be proper. For
![]() $\vartheta $
-Anosov groups though, one finds an
$\vartheta $
-Anosov groups though, one finds an
![]() ${\mathfrak a}_\vartheta $
-invariant subset which is also
${\mathfrak a}_\vartheta $
-invariant subset which is also
![]() -invariant and on which this latter action is proper (§§3.5.2 and 5.3.2). Its quotient by
-invariant and on which this latter action is proper (§§3.5.2 and 5.3.2). Its quotient by
![]() will be denoted, throughout this introduction, by
will be denoted, throughout this introduction, by
![]() $\mathcal O_{\vartheta ,\rho }.$
$\mathcal O_{\vartheta ,\rho }.$
For each
![]() $\varphi \in \mathcal Q_{\vartheta ,\rho }$
, the space
$\varphi \in \mathcal Q_{\vartheta ,\rho }$
, the space
![]() $\mathcal O_{\vartheta ,\rho }$
will carry a
$\mathcal O_{\vartheta ,\rho }$
will carry a
![]() $\varphi $
-Bowen–Margulis measure
$\varphi $
-Bowen–Margulis measure
![]() $\Omega ^\varphi $
invariant under the directional flow
$\Omega ^\varphi $
invariant under the directional flow
![]() $\unicode{x3c9} ^\varphi :\mathcal O_{\vartheta ,\rho }\to \mathcal O_{\vartheta ,\rho }$
along
$\unicode{x3c9} ^\varphi :\mathcal O_{\vartheta ,\rho }\to \mathcal O_{\vartheta ,\rho }$
along
![]() $u_\varphi \in {\mathsf {u}}_\varphi ,$
defined by (the induction on the quotient by
$u_\varphi \in {\mathsf {u}}_\varphi ,$
defined by (the induction on the quotient by
![]() of)
of)
The idea generalizing that of Sambarino [Reference Sambarino66] is that
![]() $\unicode{x3c9} ^\varphi $
is conjugated to a skew-product over a metric-Anosov flow
$\unicode{x3c9} ^\varphi $
is conjugated to a skew-product over a metric-Anosov flow
![]() $\phi ^\varphi =(\phi _t^\varphi :{\unicode{x3c7} ^{\varphi }}\to {\unicode{x3c7} ^{\varphi }})_{t\in \mathbb {R}}$
on a compact metric space
$\phi ^\varphi =(\phi _t^\varphi :{\unicode{x3c7} ^{\varphi }}\to {\unicode{x3c7} ^{\varphi }})_{t\in \mathbb {R}}$
on a compact metric space
![]() ${\unicode{x3c7} ^{\varphi }}.$
This is established in §5.12 and was previously established by Carvajales [Reference Carvajales23, Appendix] for
${\unicode{x3c7} ^{\varphi }}.$
This is established in §5.12 and was previously established by Carvajales [Reference Carvajales23, Appendix] for
![]() $\vartheta ={{{\Delta }}}.$
$\vartheta ={{{\Delta }}}.$
Remark 1.1.1. The flow
![]() $\phi ^\varphi $
plays a central role in this work. We propose to name it the
$\phi ^\varphi $
plays a central role in this work. We propose to name it the
![]() $\varphi $
-refraction flow of
$\varphi $
-refraction flow of
![]() $\rho ,$
because one may think that the projection on the base
$\rho ,$
because one may think that the projection on the base
![]() ${\unicode{x3c7} ^{\varphi }}$
refracts the orbits of
${\unicode{x3c7} ^{\varphi }}$
refracts the orbits of
![]() $\unicode{x3c9} ^\varphi $
(almost all of them wondering when
$\unicode{x3c9} ^\varphi $
(almost all of them wondering when
![]() $|\vartheta |\geq 4$
) to bind them in a compact space
$|\vartheta |\geq 4$
) to bind them in a compact space
![]() ${\unicode{x3c7} ^{\varphi }}$
and obtain non-trivial dynamical behavior. (In spite of being topologically mixing, these flows are wondering in a measurable sense, that is, almost every point belongs to a subset of positive measure with bounded return times.) Also, the term geodesic flow has too many meanings on this setting (the geodesic flow of
${\unicode{x3c7} ^{\varphi }}$
and obtain non-trivial dynamical behavior. (In spite of being topologically mixing, these flows are wondering in a measurable sense, that is, almost every point belongs to a subset of positive measure with bounded return times.) Also, the term geodesic flow has too many meanings on this setting (the geodesic flow of
![]() the geodesic flow of the locally symmetric space
the geodesic flow of the locally symmetric space
![]() the geodesic flow of a projective-Anosov representation associated to
the geodesic flow of a projective-Anosov representation associated to
![]() $\rho $
by Plucker embeddings, and so forth).
$\rho $
by Plucker embeddings, and so forth).
An ergodicity result for skew-products over metric-Anosov flows (see §2.5) gives an ergodic versus totally dissipative dichotomy for
![]() $\unicode{x3c9} ^\varphi $
according to
$\unicode{x3c9} ^\varphi $
according to
![]() $|\vartheta |\leq 2$
or
$|\vartheta |\leq 2$
or
![]() $|\vartheta |\geq 4.$
Here, the base field
$|\vartheta |\geq 4.$
Here, the base field
![]() $\mathbb {K}=\mathbb {R}$
and Zariski-density of
$\mathbb {K}=\mathbb {R}$
and Zariski-density of
![]() $\rho $
are essential, since Benoist’s [Reference Benoist8] density of Jordan projections does not hold for non-Archimedean
$\rho $
are essential, since Benoist’s [Reference Benoist8] density of Jordan projections does not hold for non-Archimedean
![]() $\mathbb {K}.$
This dichotomy is reminiscent of Sullivan’s [Reference Sullivan68] conservative versus totally dissipative dichotomy in rank 1. Observe again the untreated case
$\mathbb {K}.$
This dichotomy is reminiscent of Sullivan’s [Reference Sullivan68] conservative versus totally dissipative dichotomy in rank 1. Observe again the untreated case
![]() $|\vartheta |=3.$
$|\vartheta |=3.$
These dynamical properties of
![]() $\unicode{x3c9} ^\varphi $
imply the following. The set
$\unicode{x3c9} ^\varphi $
imply the following. The set
![]() $\mathcal K(\unicode{x3c9} ^\varphi )$
of points in
$\mathcal K(\unicode{x3c9} ^\varphi )$
of points in
![]() $\mathcal O_{\vartheta ,\rho }$
, whose future orbit returns unboundedly to some open bounded set, has either zero
$\mathcal O_{\vartheta ,\rho }$
, whose future orbit returns unboundedly to some open bounded set, has either zero
![]() $\Omega ^\varphi $
-mass if
$\Omega ^\varphi $
-mass if
![]() $|\vartheta |\geq 4$
or its complement has zero
$|\vartheta |\geq 4$
or its complement has zero
![]() $\Omega ^\varphi $
-mass if
$\Omega ^\varphi $
-mass if
![]() $|\vartheta |\leq 2.$
$|\vartheta |\leq 2.$
The key feature now is to relate
![]() ${\mathsf {u}}_\varphi $
-conical points with the set
${\mathsf {u}}_\varphi $
-conical points with the set
![]() $\mathcal K(\unicode{x3c9} ^\varphi ).$
This is attained in Lemma 5.13.3 where it is shown that a triple
$\mathcal K(\unicode{x3c9} ^\varphi ).$
This is attained in Lemma 5.13.3 where it is shown that a triple
![]() $(x,y,v)\in \mathcal F^{(2)}_\vartheta \times {\mathfrak a}_\vartheta $
projects to
$(x,y,v)\in \mathcal F^{(2)}_\vartheta \times {\mathfrak a}_\vartheta $
projects to
![]() $\mathcal K(\unicode{x3c9} ^\varphi )$
if and only if y is
$\mathcal K(\unicode{x3c9} ^\varphi )$
if and only if y is
![]() ${\mathsf {u}}_\varphi $
-conical. The previous dynamical dichotomy gives then the dichotomy on the
${\mathsf {u}}_\varphi $
-conical. The previous dynamical dichotomy gives then the dichotomy on the
![]() $\mu ^\varphi $
-measure on conical points:
$\mu ^\varphi $
-measure on conical points:
The global strategy of our proof is different from the analog result of Burger et al [Reference Burger, Landesberg, Lee and Oh20]. While, inspired by them, we also use a mixing result. The use of a Dirichlet–Poincaré series along tubes does not play any role in the proof of Theorem B, nor on the ergodicity dichotomy for directional flows.
Let us end §1 by observing that both Burger et al [Reference Burger, Landesberg, Lee and Oh20] and Chow and Sarkar [Reference Chow and Sarkar25] prove dynamical statements on
![]() (as opposed to
(as opposed to
![]() ).
).
1.2 Plan of the paper
In §2, we recall some basic facts about the ergodic theory of metric-Anosov flows, and then study translation cocycles over them. Section 3 deals with a Ledrappier correspondence for word-hyperbolic groups whose Gromov–Mineyev geodesic flow is metric-Anosov. We will mainly apply these results to the Buseman–Iwasawa cocycle of
![]() ${\mathsf {G}}.$
For applications to other cocycles, the reader may check the work of Carvajales [Reference Carvajales22, Reference Carvajales23].
${\mathsf {G}}.$
For applications to other cocycles, the reader may check the work of Carvajales [Reference Carvajales22, Reference Carvajales23].
We then recall in §4 necessary definitions on semi-simple algebraic groups over a local field and deal with Anosov representations in §5. We explain in this section how the Ledrappier correspondence applies in this setting to give, mainly:
-
• uniqueness results on the Patterson–Sullivan measures;
-
• precise dynamical information on the directional flows
 $\unicode{x3c9} ^\varphi .$
$\unicode{x3c9} ^\varphi .$
2 Skew-products over metric-Anosov flows
Throughout this section, we let X be a compact metric space and V a finite dimension real vector space.
2.1 Thermodynamic formalism and reparameterizations
Let
![]() $\phi =(\phi _t:X \to X)_{t\in \mathbb {R}}$
be a continuous flow without fixed points. The space of
$\phi =(\phi _t:X \to X)_{t\in \mathbb {R}}$
be a continuous flow without fixed points. The space of
![]() $\phi $
-invariant probability measures on X is denoted by
$\phi $
-invariant probability measures on X is denoted by
![]() $\mathcal M^\phi .$
It is a convex, weakly compact subset of
$\mathcal M^\phi .$
It is a convex, weakly compact subset of
![]() $C^*(X),$
the dual space to the space of continuous functions equipped with the uniform topology. The metric entropy of
$C^*(X),$
the dual space to the space of continuous functions equipped with the uniform topology. The metric entropy of
![]() $m\in \mathcal M^\phi $
will be denoted by
$m\in \mathcal M^\phi $
will be denoted by
![]() $h(\phi ,m).$
Its definition can be found in Aaronson’s book [Reference Aaronson1]. Via the variational principle, we will define the topological pressure (or just pressure) of a function
$h(\phi ,m).$
Its definition can be found in Aaronson’s book [Reference Aaronson1]. Via the variational principle, we will define the topological pressure (or just pressure) of a function
![]() $f:X\to \mathbb {R}$
as the quantity
$f:X\to \mathbb {R}$
as the quantity
 $$ \begin{align}P(\phi,f)= \sup_{m\in\mathcal M^{\phi}} \bigg(h(\phi,m)+\int_X f\,dm\bigg).\end{align} $$
$$ \begin{align}P(\phi,f)= \sup_{m\in\mathcal M^{\phi}} \bigg(h(\phi,m)+\int_X f\,dm\bigg).\end{align} $$
A probability measure m realizing the least upper bound is called an equilibrium state of
![]() $f.$
An equilibrium state for
$f.$
An equilibrium state for
![]() $f\equiv 0$
is called a measure of maximal entropy, and its entropy is called the topological entropy of
$f\equiv 0$
is called a measure of maximal entropy, and its entropy is called the topological entropy of
![]() $\phi ,$
denoted by
$\phi ,$
denoted by
![]() $h(\phi ).$
$h(\phi ).$
Let
![]() $f:X\to \mathbb {R}_{>0}$
be continuous. For every
$f:X\to \mathbb {R}_{>0}$
be continuous. For every
![]() $x\in X$
, the function
$x\in X$
, the function
![]() $k_f:X\times \mathbb {R}\to \mathbb {R},$
defined by
$k_f:X\times \mathbb {R}\to \mathbb {R},$
defined by
![]() $k_f(x,t)=\int _0^tf(\phi _sx)\,ds,$
is an increasing homeomorphism of
$k_f(x,t)=\int _0^tf(\phi _sx)\,ds,$
is an increasing homeomorphism of
![]() $\mathbb {R}.$
There is thus a continuous function
$\mathbb {R}.$
There is thus a continuous function
![]() $\alpha _f:X\times \mathbb {R}\to \mathbb {R}$
such that for all
$\alpha _f:X\times \mathbb {R}\to \mathbb {R}$
such that for all
![]() $(x,t)\in X\times \mathbb {R},$
$(x,t)\in X\times \mathbb {R},$
The reparameterization of
![]() $\phi $
by
$\phi $
by
![]() $f:X\to \mathbb {R}_{>0}$
is the flow
$f:X\to \mathbb {R}_{>0}$
is the flow
![]() $\phi ^f\!=(\phi ^f_t\!:X \to X)_{t\in \mathbb {R}}$
defined, for all
$\phi ^f\!=(\phi ^f_t\!:X \to X)_{t\in \mathbb {R}}$
defined, for all
![]() $(x,t)\in X\times \mathbb {R}$
, by
$(x,t)\in X\times \mathbb {R}$
, by
The Abramov transform of
![]() $m\in \mathcal M^\phi $
is the probability measure
$m\in \mathcal M^\phi $
is the probability measure
![]() $m^\#\in \mathcal M^{\phi ^f\!}$
defined by
$m^\#\in \mathcal M^{\phi ^f\!}$
defined by
 $$ \begin{align}m^\#=\frac{f\cdot m}{\int f\,dm}.\end{align} $$
$$ \begin{align}m^\#=\frac{f\cdot m}{\int f\,dm}.\end{align} $$
One has the following lemma.
Lemma 2.1.1. (Sambarino [Reference Sambarino65, Lemma 2.4])
Let
![]() $f:X\to \mathbb {R}_{>0}$
be a continuous function. Assume the equation
$f:X\to \mathbb {R}_{>0}$
be a continuous function. Assume the equation
has a finite positive solution
![]() $h,$
then h is the topological entropy of
$h,$
then h is the topological entropy of
![]() $\phi ^f\!.$
Conversely, if
$\phi ^f\!.$
Conversely, if
![]() $h(\phi ^f\!)$
is finite, then it is a solution to the last equation. In this situation, the Abramov transform induces a bijection between the set of equilibrium states of
$h(\phi ^f\!)$
is finite, then it is a solution to the last equation. In this situation, the Abramov transform induces a bijection between the set of equilibrium states of
![]() $-hf$
and the set of probability measures maximizing entropy for
$-hf$
and the set of probability measures maximizing entropy for
![]() $\phi ^f\!.$
$\phi ^f\!.$
Two continuous maps
![]() $f,g:X\to V$
are Livšic-cohomologous if there exists a
$f,g:X\to V$
are Livšic-cohomologous if there exists a
![]() $U:X\to ~V$
of class
$U:X\to ~V$
of class
![]() $\operatorname {\mathrm {C}}^1$
in the direction of the flow (that is, such that if for every
$\operatorname {\mathrm {C}}^1$
in the direction of the flow (that is, such that if for every
![]() $x\in X,$
the map
$x\in X,$
the map
![]() $t\mapsto U(\phi _tx)$
is of class
$t\mapsto U(\phi _tx)$
is of class
![]() $\operatorname {\mathrm {C}}^1$
and the map
$\operatorname {\mathrm {C}}^1$
and the map
![]() $x\mapsto {\partial }/{\partial t}|_{t=0}U(\phi _tx)$
is continuous), such that for all
$x\mapsto {\partial }/{\partial t}|_{t=0}U(\phi _tx)$
is continuous), such that for all
![]() $x\in X$
, one has
$x\in X$
, one has
 $$ \begin{align*}f(x)-g(x)=\frac{\partial}{\partial t}\bigg|_{t=0} U(\phi_tx).\end{align*} $$
$$ \begin{align*}f(x)-g(x)=\frac{\partial}{\partial t}\bigg|_{t=0} U(\phi_tx).\end{align*} $$
Remark 2.1.2. If f and g are real-valued and Livšic-cohomologous, then
![]() $P(\phi ,f)=P(\phi ,g).$
$P(\phi ,f)=P(\phi ,g).$
2.2 Metric-Anosov flows I: Livšic-cohomology
Metric-Anosov flows are a metric version of what is commonly known as hyperbolic flows. The former are called Smale flows by Pollicott [Reference Pollicott56], who transferred to this more general setting the classical theory carried out for the latter. We recall here their definition and some well-known facts on their ergodic theory needed in what follows. Throughout this subsection, we will further assume that
![]() $\phi $
is Hölder-continuous with an exponent independent of
$\phi $
is Hölder-continuous with an exponent independent of
![]() $t,$
that it is transitive, that it has a dense orbit, and that it is metric-Anosov.
$t,$
that it is transitive, that it has a dense orbit, and that it is metric-Anosov.
For
![]() $\varepsilon>0$
, the local stable/unstable set of x are (respectively)
$\varepsilon>0$
, the local stable/unstable set of x are (respectively)
 $$ \begin{align*}W^{{\mathrm{s}}}_{\varepsilon}(x) & =\{y\in X:d(\phi_tx,\phi_t y)\leq\varepsilon \text{ for all } t>0\textrm{ and }d(\phi_tx,\phi_t y)\to0\textrm{ as }t\to\infty\},\\ W^{{\mathrm{u}}}_{\varepsilon}(x) & =\{y\in X:d(\phi_{-t}x,\phi_{-t} y)\leq\varepsilon \text{ for all } t>0\textrm{ and }d(\phi_{-t}x,\phi_{-t} y)\to0\textrm{ as }t\to\infty\}.\end{align*} $$
$$ \begin{align*}W^{{\mathrm{s}}}_{\varepsilon}(x) & =\{y\in X:d(\phi_tx,\phi_t y)\leq\varepsilon \text{ for all } t>0\textrm{ and }d(\phi_tx,\phi_t y)\to0\textrm{ as }t\to\infty\},\\ W^{{\mathrm{u}}}_{\varepsilon}(x) & =\{y\in X:d(\phi_{-t}x,\phi_{-t} y)\leq\varepsilon \text{ for all } t>0\textrm{ and }d(\phi_{-t}x,\phi_{-t} y)\to0\textrm{ as }t\to\infty\}.\end{align*} $$
Definition 2.2.1. (Metric-Anosov)
The flow
![]() $\phi $
is metric-Anosov if the following hold.
$\phi $
is metric-Anosov if the following hold.
-
• (Exponential decay) There exist positive constants
 $C, \unicode{x3bb} $
and
$C, \unicode{x3bb} $
and
 $\varepsilon $
such that for every
$\varepsilon $
such that for every
 $x\in ~X,$
every
$x\in ~X,$
every
 $y\in W^{{\mathrm {s}}}_\varepsilon (x)$
, and every
$y\in W^{{\mathrm {s}}}_\varepsilon (x)$
, and every
 $t>0$
, one has and such that for every
$t>0$
, one has and such that for every $$ \begin{align*}d(\phi_tx,\phi_ty)\leq Ce^{-\unicode{x3bb} t},\end{align*} $$
$$ \begin{align*}d(\phi_tx,\phi_ty)\leq Ce^{-\unicode{x3bb} t},\end{align*} $$
 $y\in W^{{\mathrm {u}}}_\varepsilon (x)$
, one has
$y\in W^{{\mathrm {u}}}_\varepsilon (x)$
, one has
 $d(\phi _{-t}x,\phi _{-t}y)\leq Ce^{-\unicode{x3bb} t}.$
$d(\phi _{-t}x,\phi _{-t}y)\leq Ce^{-\unicode{x3bb} t}.$
-
• (Local product structure) There exist
 $\delta ,\varepsilon>0$
and a Hölder-continuous map such that
$\delta ,\varepsilon>0$
and a Hölder-continuous map such that $$ \begin{align*}\unicode{x3bd}:\{(x,y)\in X\times X:d(x,y)<\delta\}\to \mathbb{R}\end{align*} $$
$$ \begin{align*}\unicode{x3bd}:\{(x,y)\in X\times X:d(x,y)<\delta\}\to \mathbb{R}\end{align*} $$
 $\unicode{x3bd} (x,y)$
is the unique value
$\unicode{x3bd} (x,y)$
is the unique value
 $\unicode{x3bd} $
such that
$\unicode{x3bd} $
such that
 $W^{{\mathrm {u}}}_\varepsilon (\phi _\unicode{x3bd} x)\cap W^{{\mathrm {s}}}_\varepsilon (y)$
is non-empty, and consists of exactly one point, called
$W^{{\mathrm {u}}}_\varepsilon (\phi _\unicode{x3bd} x)\cap W^{{\mathrm {s}}}_\varepsilon (y)$
is non-empty, and consists of exactly one point, called
 $\langle x,y\rangle ;$
and for every
$\langle x,y\rangle ;$
and for every
 $x\in X$
, the map given by
$x\in X$
, the map given by $$ \begin{align*}W^{{\mathrm{s}}}_\varepsilon(x)\times W^{{\mathrm{u}}}_\varepsilon(x)\times(-\delta,\delta)\to X,\end{align*} $$
$$ \begin{align*}W^{{\mathrm{s}}}_\varepsilon(x)\times W^{{\mathrm{u}}}_\varepsilon(x)\times(-\delta,\delta)\to X,\end{align*} $$
 $(y,z,t)\mapsto \phi _t(\langle y,z\rangle ),$
is a Hölder-homeomorphism onto an open neighborhood of
$(y,z,t)\mapsto \phi _t(\langle y,z\rangle ),$
is a Hölder-homeomorphism onto an open neighborhood of
 $x.$
$x.$
A translation cocycle over
![]() $\phi $
is a map
$\phi $
is a map
![]() $k: X\times \mathbb {R} \to V$
such that for every
$k: X\times \mathbb {R} \to V$
such that for every
![]() $x\in X$
and
$x\in X$
and
![]() $t,s\in \mathbb {R},$
one has
$t,s\in \mathbb {R},$
one has
and such that the map
![]() $k(\cdot ,t)$
is Hölder-continuous with exponent independent of t and with bounded multiplicative constant when t remains on a bounded set. Two translation cocycles
$k(\cdot ,t)$
is Hölder-continuous with exponent independent of t and with bounded multiplicative constant when t remains on a bounded set. Two translation cocycles
![]() $k_1$
and
$k_1$
and
![]() $k_2$
are Livšic-cohomologous if there exists a continuous map
$k_2$
are Livšic-cohomologous if there exists a continuous map
![]() $U:X\to V,$
such that for all
$U:X\to V,$
such that for all
![]() $x\in X$
and
$x\in X$
and
![]() $t\in \mathbb {R}$
, one has
$t\in \mathbb {R}$
, one has
If k is a translation cocycle, then the period for k of a periodic orbit
![]() $\tau $
is
$\tau $
is
for any
![]() $x\in \tau .$
The marked spectrum
$x\in \tau .$
The marked spectrum
![]() $\tau \mapsto \ell _k(\tau )$
is a cohomological invariant that uniquely determines its class.
$\tau \mapsto \ell _k(\tau )$
is a cohomological invariant that uniquely determines its class.
Theorem 2.2.2. (Livšic [Reference Livšic47])
Let
![]() $k:X\times \mathbb {R}\to V$
be a translation cocycle. If
$k:X\times \mathbb {R}\to V$
be a translation cocycle. If
![]() $\ell _k(\tau )=0$
for every periodic orbit
$\ell _k(\tau )=0$
for every periodic orbit
![]() $\tau ,$
then k is Livšic-cohomologous to
$\tau ,$
then k is Livšic-cohomologous to
![]() $0.$
$0.$
Observe that if
![]() $f:X\to V$
is Hölder-continuous, then the map
$f:X\to V$
is Hölder-continuous, then the map
 $$ \begin{align*}k_f(x,t)=\int_0^tf(\phi_sx)\,ds\end{align*} $$
$$ \begin{align*}k_f(x,t)=\int_0^tf(\phi_sx)\,ds\end{align*} $$
is a translation cocycle. Two such functions are Livšic-cohomologous if and only if the associated cocycles are, and the period of f on
![]() $\tau $
is, for any
$\tau $
is, for any
![]() $x\in \tau ,$
$x\in \tau ,$
It turns out that every cocycle is Livšic-cohomologous to a cocycle of the form
![]() $k_f$
.
$k_f$
.
Corollary 2.2.3. (Sambarino [Reference Sambarino66, Lemma 2.6])
If
![]() $k:X\times \mathbb {R}\to V$
is a translation cocycle, then there exists a Hölder-continuous
$k:X\times \mathbb {R}\to V$
is a translation cocycle, then there exists a Hölder-continuous
![]() $f:X\to V$
such that
$f:X\to V$
such that
![]() $ k$
and
$ k$
and
![]() $k_f$
are Livšic-cohomologous.
$k_f$
are Livšic-cohomologous.
Proof. For any
![]() $\kappa>0,$
the function
$\kappa>0,$
the function
![]() $j(x,t)=1/{2\kappa }\int _{-\kappa }^\kappa k(x,t+s)\,ds$
is differentiable on the second variable. Let
$j(x,t)=1/{2\kappa }\int _{-\kappa }^\kappa k(x,t+s)\,ds$
is differentiable on the second variable. Let
![]() $f(x)=(\partial /\partial s)|_{s=0}j(x,s).$
Then,
$f(x)=(\partial /\partial s)|_{s=0}j(x,s).$
Then,
 $$ \begin{align*}k_f(x,t)&=\int_0^tf(\phi_ux)\,du =\int_0^t\frac{\partial}{\partial s}\bigg|_{s=0}j(\phi_ux,s)\,du\\ & =\int_0^t\frac{\partial}{\partial s}\bigg|_{s=0}j(x,s+u)\,du = j(x,t)-j(x,0),\end{align*} $$
$$ \begin{align*}k_f(x,t)&=\int_0^tf(\phi_ux)\,du =\int_0^t\frac{\partial}{\partial s}\bigg|_{s=0}j(\phi_ux,s)\,du\\ & =\int_0^t\frac{\partial}{\partial s}\bigg|_{s=0}j(x,s+u)\,du = j(x,t)-j(x,0),\end{align*} $$
so the period
![]() $k_f(x,p(\tau ))=j(x,p(\tau ))-j(x,0)=k(x,p(\tau )).$
By Theorem 2.2.2, the cocycles k and
$k_f(x,p(\tau ))=j(x,p(\tau ))-j(x,0)=k(x,p(\tau )).$
By Theorem 2.2.2, the cocycles k and
![]() $k_f$
are thus Livšic-cohomologous.
$k_f$
are thus Livšic-cohomologous.
We record also the following immediate consequence of Livšic’s theorem.
Remark 2.2.4. The space of functions Livšic-cohomologous to a strictly positive function is an (open cone on an) infinite dimensional space.
In this context, much more information can be stated about the pressure function. Recall that the space
![]() $\operatorname {\mathrm {Holder}}^\alpha (X)$
of real valued
$\operatorname {\mathrm {Holder}}^\alpha (X)$
of real valued
![]() $\alpha $
-Hölder functions is naturally a Banach space when equipped with the norm
$\alpha $
-Hölder functions is naturally a Banach space when equipped with the norm
 $$ \begin{align*}\|f\|_\alpha=\|f\|_\infty+\sup_{x\neq y}\frac{|f(x)-f(y)|}{d(x,y)^\alpha}.\end{align*} $$
$$ \begin{align*}\|f\|_\alpha=\|f\|_\infty+\sup_{x\neq y}\frac{|f(x)-f(y)|}{d(x,y)^\alpha}.\end{align*} $$
Proposition 2.2.5. (Bowen and Ruelle [Reference Bowen and Ruelle16] and Parry and Pollicott [Reference Parry and Pollicott53, Proposition 4.10])
The function
![]() $P(\phi ,\cdot )$
is analytic on
$P(\phi ,\cdot )$
is analytic on
![]() $\operatorname {\mathrm {Holder}}^\alpha (X).$
If
$\operatorname {\mathrm {Holder}}^\alpha (X).$
If
![]() $f,g\in \operatorname {\mathrm {Holder}}^\alpha (X),$
then
$f,g\in \operatorname {\mathrm {Holder}}^\alpha (X),$
then
 $$ \begin{align*}\frac{\partial}{\partial t}\bigg|_{t=0}P(\phi,f+tg)=\int gdm_f,\end{align*} $$
$$ \begin{align*}\frac{\partial}{\partial t}\bigg|_{t=0}P(\phi,f+tg)=\int gdm_f,\end{align*} $$
where
![]() $m_f$
is the equilibrium state of
$m_f$
is the equilibrium state of
![]() $f,$
and the function
$f,$
and the function
![]() $t\mapsto P(\phi ,f+tg)$
is strictly convex unless g is Livšic-cohomologous to a constant. Finally, one also has
$t\mapsto P(\phi ,f+tg)$
is strictly convex unless g is Livšic-cohomologous to a constant. Finally, one also has
 $$ \begin{align}P(\phi,f)=\limsup_{t\to\infty}\frac1t\log\sum_{\tau:p(\tau)\leq t}e^{\ell_\tau(f)}.\end{align} $$
$$ \begin{align}P(\phi,f)=\limsup_{t\to\infty}\frac1t\log\sum_{\tau:p(\tau)\leq t}e^{\ell_\tau(f)}.\end{align} $$
Let
![]() $f\in \operatorname {\mathrm {Holder}}^\alpha (X)$
have non-negative (and not all vanishing) periods and define its entropy by
$f\in \operatorname {\mathrm {Holder}}^\alpha (X)$
have non-negative (and not all vanishing) periods and define its entropy by
 $$ \begin{align*}\mathscr h_f=\limsup_{s\to\infty}\frac1s\log\#\bigg\{\tau\textrm{ periodic}:\int_\tau f\leq s\bigg\}\in(0,\infty].\end{align*} $$
$$ \begin{align*}\mathscr h_f=\limsup_{s\to\infty}\frac1s\log\#\bigg\{\tau\textrm{ periodic}:\int_\tau f\leq s\bigg\}\in(0,\infty].\end{align*} $$
Remark 2.2.6. Observe that
![]() $\mathscr h_f$
is necessarily
$\mathscr h_f$
is necessarily
![]() $>0$
since f must have a positive maximum and
$>0$
since f must have a positive maximum and
![]() $h(\phi )>0.$
$h(\phi )>0.$
One has the following lemma.
Lemma 2.2.7. (Ledrappier [Reference Ledrappier44, Lemma 1] and Sambarino [Reference Sambarino65, Lemma 3.8])
Consider a Hölder-continuous function
![]() $f:X\to \mathbb {R}$
with non-negative periods. Then the following statements are equivalent:
$f:X\to \mathbb {R}$
with non-negative periods. Then the following statements are equivalent:
-
• the function f is Livšic-cohomologous to a positive Hölder-continuous function;
-
• there exists
 $\kappa>0$
such that
$\kappa>0$
such that
 $\int _\tau f>\kappa p(\tau )$
for every periodic orbit
$\int _\tau f>\kappa p(\tau )$
for every periodic orbit
 $\tau ;$
$\tau ;$
-
• the entropy
 $\mathscr h_f$
is finite;
$\mathscr h_f$
is finite; -
• the function
 $t\mapsto P(\phi , -tf)$
has a positive zero, in which case is
$t\mapsto P(\phi , -tf)$
has a positive zero, in which case is
 $\mathscr h_f.$
$\mathscr h_f.$
Let us fix an exponent
![]() $\alpha $
and consider the cone
$\alpha $
and consider the cone
![]() $\operatorname {\mathrm {Holder}}^\alpha _+(X,\mathbb {R})$
of Hölder-continuous functions that are Livšic-cohomologous to a strictly positive function. The implicit function theorem for Banach spaces (see [Reference Akerkar2]) and the explicit formula for the derivative of pressure (Proposition 2.2.5) give the following corollary.
$\operatorname {\mathrm {Holder}}^\alpha _+(X,\mathbb {R})$
of Hölder-continuous functions that are Livšic-cohomologous to a strictly positive function. The implicit function theorem for Banach spaces (see [Reference Akerkar2]) and the explicit formula for the derivative of pressure (Proposition 2.2.5) give the following corollary.
Lemma 2.2.8. The entropy map
![]() $\mathscr h:\operatorname {\mathrm {Holder}}^\alpha _+(X,\mathbb {R})\to \mathbb {R}_+$
is analytic.
$\mathscr h:\operatorname {\mathrm {Holder}}^\alpha _+(X,\mathbb {R})\to \mathbb {R}_+$
is analytic.
2.3 Metric-Anosov flows II: ergodic theory
A fundamental tool for studying the ergodic theory of metric-Anosov systems is the existence of a Markov coding.
Let
![]() $\Sigma $
be an irreducible sub-shift of finite type equipped with its shift transformation
$\Sigma $
be an irreducible sub-shift of finite type equipped with its shift transformation
![]() $\sigma :\Sigma \to \Sigma ,$
and
$\sigma :\Sigma \to \Sigma ,$
and
![]() $r:\Sigma \to \mathbb {R}_{>0}$
be Hölder-continuous. Let
$r:\Sigma \to \mathbb {R}_{>0}$
be Hölder-continuous. Let
![]() $\hat r:\Sigma \times \mathbb {R}\to \Sigma \times \mathbb {R}$
be defined as
$\hat r:\Sigma \times \mathbb {R}\to \Sigma \times \mathbb {R}$
be defined as
and consider the quotient space
![]() It is equipped with the flow
It is equipped with the flow
![]() induced on the quotient by the translation flow.
induced on the quotient by the translation flow.
Definition 2.3.1. (Markov coding)
A triplet
![]() $(\Sigma ,\pi ,r)$
is a Markov coding for
$(\Sigma ,\pi ,r)$
is a Markov coding for
![]() $\phi $
if
$\phi $
if
![]() $\Sigma $
and r are as above,
$\Sigma $
and r are as above,
![]() $\pi :\Sigma \to X$
is Hölder-continuous, and the function
$\pi :\Sigma \to X$
is Hölder-continuous, and the function
![]() $\pi _r:\Sigma \times \mathbb {R}\to X$
defined as
$\pi _r:\Sigma \times \mathbb {R}\to X$
defined as
verifies the following conditions:
-
(i)
 $\pi _r$
is Hölder-continuous, surjective, and
$\pi _r$
is Hölder-continuous, surjective, and
 $\hat r$
-invariant, it passes then to the quotient
$\hat r$
-invariant, it passes then to the quotient

-
(ii)
 is bounded-to-one and injective on a residual set which is of full measure for every ergodic
is bounded-to-one and injective on a residual set which is of full measure for every ergodic
 $\unicode{x3c3} ^r$
-invariant measure of total support;
$\unicode{x3c3} ^r$
-invariant measure of total support; -
(iii) for every
 $t\in \mathbb {R}$
, one has
$t\in \mathbb {R}$
, one has
 $\pi _r\unicode{x3c3} ^r_t=\phi _t\pi _r.$
$\pi _r\unicode{x3c3} ^r_t=\phi _t\pi _r.$
The following result has a long history, see for example the works of Bowen [Reference Bowen14, Reference Bowen15], Ratner [Reference Ratner63], Pollicott [Reference Pollicott56], and more recently Constantine, Lafont, and Thompson [Reference Constantine, Lafont and Thompson27].
Theorem 2.3.2. (Existence of coding)
A transitive metric-Anosov flow admits a Markov coding.
The above is a fundamental tool to obtain the following, see for example the works of Bowen and Ruelle [Reference Bowen and Ruelle16], Parry and Pollicott [Reference Parry and Pollicott53], and more recently Giulietti et al [Reference Giulietti, Kloeckner, Lopes and Marcon31]. Recall from §2.1 the definition of equilibrium state.
Theorem 2.3.3. (Uniqueness of equilibrium states)
Let
![]() $f:X\to \mathbb {R}$
be Hölder-continuous. Then there exists a unique equilibrium state for
$f:X\to \mathbb {R}$
be Hölder-continuous. Then there exists a unique equilibrium state for
![]() $f,$
denoted by
$f,$
denoted by
![]() $m_f;$
it is an ergodic measure. If
$m_f;$
it is an ergodic measure. If
![]() $g:X\to \mathbb {R}$
is also Hölder, then
$g:X\to \mathbb {R}$
is also Hölder, then
![]() $m_g\ll m_f$
if and only if
$m_g\ll m_f$
if and only if
![]() $f-g$
is Livšic-cohomologous to a constant function, in which case,
$f-g$
is Livšic-cohomologous to a constant function, in which case,
![]() $m_g=m_f.$
The function
$m_g=m_f.$
The function
![]() $f\mapsto m_f,$
defined on the space of Hölder-continuous functions with fixed exponent, is analytic. (We emphasize that the space of measures is endowed with the differentiable structure induced by being the dual space of continuous functions.)
$f\mapsto m_f,$
defined on the space of Hölder-continuous functions with fixed exponent, is analytic. (We emphasize that the space of measures is endowed with the differentiable structure induced by being the dual space of continuous functions.)
A final fact we will require in this setting (introduced by Margulis [Reference Margulis48]) is the decomposition of the measure of maximal entropy along the stable/central-unstable sets of
![]() $\phi .$
$\phi .$
The stable/unstable leaf of x is
 $$ \begin{align*} W^{\mathrm{s}}(x) & = \bigcup_{t\in\mathbb{R}_+} \phi_{-t}(W^{{\mathrm{s}}}_\varepsilon(\phi_tx)),\\ W^{{\mathrm{u}}}(x) & = \bigcup_{t\in\mathbb{R}_+} \phi_{t}(W^{{\mathrm{u}}}_\varepsilon(\phi_{-t}x)),\end{align*} $$
$$ \begin{align*} W^{\mathrm{s}}(x) & = \bigcup_{t\in\mathbb{R}_+} \phi_{-t}(W^{{\mathrm{s}}}_\varepsilon(\phi_tx)),\\ W^{{\mathrm{u}}}(x) & = \bigcup_{t\in\mathbb{R}_+} \phi_{t}(W^{{\mathrm{u}}}_\varepsilon(\phi_{-t}x)),\end{align*} $$
and the central stable/unstable leaf is (respectively) the
![]() $\phi $
-orbit of
$\phi $
-orbit of
![]() $W^{\mathrm {s}}(x)$
(respectively
$W^{\mathrm {s}}(x)$
(respectively
![]() $W^{{\mathrm {u}}}(x)$
). These sets are independent of (any small enough)
$W^{{\mathrm {u}}}(x)$
). These sets are independent of (any small enough)
![]() $\varepsilon $
(that is smaller than the
$\varepsilon $
(that is smaller than the
![]() $\varepsilon $
given by Definition 2.2.1).
$\varepsilon $
given by Definition 2.2.1).
One has the following, see for example the works of Margulis [Reference Margulis49], Pollicott [Reference Pollicott55] for a construction via Markov codings or Katok and Hasselblatt’s book [Reference Katok and Hasselblatt41, §5 of Ch. 20] for the discrete-time case.
Theorem 2.3.4. (Margulis description)
For each
![]() $x\in X$
, there exists a measure
$x\in X$
, there exists a measure
![]() $\mu _x^{{\mathrm {s}}}$
on the stable leaf
$\mu _x^{{\mathrm {s}}}$
on the stable leaf
![]() $W^{\mathrm {s}}(x)$
and a measure
$W^{\mathrm {s}}(x)$
and a measure
![]() $\mu _x^{\mathrm {cu}}$
on the central unstable leaf such that:
$\mu _x^{\mathrm {cu}}$
on the central unstable leaf such that:
-
• for all
 $t>0$
and all measurable
$t>0$
and all measurable
 $U\subset W^{{\mathrm {s}}}(x)$
, one has (6)
$U\subset W^{{\mathrm {s}}}(x)$
, one has (6) $$ \begin{align}\mu_{\phi_tx}^{\mathrm{s}}(\phi_tU)=e^{-h(\phi)t}\mu_{x}^{\mathrm{s}}(U); \end{align} $$
$$ \begin{align}\mu_{\phi_tx}^{\mathrm{s}}(\phi_tU)=e^{-h(\phi)t}\mu_{x}^{\mathrm{s}}(U); \end{align} $$
-
• the local product structure in Definition 2.2 induces a local isomorphism between the measure
 $\mu _x^{\mathrm {s}}\otimes \mu ^{\mathrm {cu}}_x$
and the measure of maximal entropy of
$\mu _x^{\mathrm {s}}\otimes \mu ^{\mathrm {cu}}_x$
and the measure of maximal entropy of
 $\phi .$
$\phi .$
The family of measures is unique in the following sense. If
![]() $\nu _x^{\mathrm {s}}$
and
$\nu _x^{\mathrm {s}}$
and
![]() $\nu _x^{\mathrm {cu}}$
are also a family of measures along the stable and central-unstable leafs of x such that the product
$\nu _x^{\mathrm {cu}}$
are also a family of measures along the stable and central-unstable leafs of x such that the product
![]() $\nu _x^{\mathrm {s}}\otimes \nu _x^{\mathrm {cu}}$
is locally isomorphic to a
$\nu _x^{\mathrm {s}}\otimes \nu _x^{\mathrm {cu}}$
is locally isomorphic to a
![]() $\phi $
-invariant measure and
$\phi $
-invariant measure and
![]() $\nu ^{{\mathrm {s}}}_x$
verifies equation (6) with some arbitrary fixed
$\nu ^{{\mathrm {s}}}_x$
verifies equation (6) with some arbitrary fixed
![]() $\delta>0$
(instead of
$\delta>0$
(instead of
![]() $h(\phi )$
), then
$h(\phi )$
), then
![]() $\delta =h(\phi ), \nu ^{{\mathrm {s}}}_x=\mu ^{{\mathrm {s}}}_x$
, and
$\delta =h(\phi ), \nu ^{{\mathrm {s}}}_x=\mu ^{{\mathrm {s}}}_x$
, and
![]() $\mu ^{\mathrm {cu}}_x=\nu ^{\mathrm {cu}}_x.$
$\mu ^{\mathrm {cu}}_x=\nu ^{\mathrm {cu}}_x.$
2.4 Skew-products over sub-shifts
Consider now the two-sided subshift
![]() $\Sigma $
and let
$\Sigma $
and let
![]() ${\mathsf {K}}:\Sigma \to V$
be Hölder-continuous.
${\mathsf {K}}:\Sigma \to V$
be Hölder-continuous.
Definition 2.4.1. We say that
![]() ${\mathsf {K}}$
is non-arithmetic if the group spanned by the periods of
${\mathsf {K}}$
is non-arithmetic if the group spanned by the periods of
![]() ${\mathsf {K}}$
is dense in
${\mathsf {K}}$
is dense in
![]() $V.$
$V.$
The skew-product system is defined by
![]() $f=f^{\mathsf {K}}:\Sigma \times V\to \Sigma \times V$
$f=f^{\mathsf {K}}:\Sigma \times V\to \Sigma \times V$
If
![]() $\nu $
is a
$\nu $
is a
![]() $\sigma $
-invariant probability measure on
$\sigma $
-invariant probability measure on
![]() $\Sigma $
, then the measure
$\Sigma $
, then the measure
![]() is f-invariant.
is f-invariant.
The following proposition seems to be well known but we have not been able to find a specific reference in the literature, for completeness, we added a short proof in Appendix A.
Proposition 2.4.2. Let
![]() $\Sigma $
be a two-sided sub-shift,
$\Sigma $
be a two-sided sub-shift,
![]() $\nu $
be an equilibrium state of some Hölder potential, and
$\nu $
be an equilibrium state of some Hölder potential, and
![]() ${\mathsf {K}}:\Sigma \to \mathbb {R}$
a non-arithmetic Hölder-continuous function with
${\mathsf {K}}:\Sigma \to \mathbb {R}$
a non-arithmetic Hölder-continuous function with
![]() $\int {\mathsf {K}}d\nu =0.$
Then the skew-product
$\int {\mathsf {K}}d\nu =0.$
Then the skew-product
![]() $f^{\mathsf {K}}:\Sigma \times \mathbb {R}\to \Sigma \times \mathbb {R}$
is ergodic with respect to
$f^{\mathsf {K}}:\Sigma \times \mathbb {R}\to \Sigma \times \mathbb {R}$
is ergodic with respect to
![]()
We record also the following classical lemma. Let us say that a subset of
![]() $\Sigma \times V$
is bounded if it has compact closure, and that it has total mass (with respect to
$\Sigma \times V$
is bounded if it has compact closure, and that it has total mass (with respect to
![]() ) if its complement has measure zero. As the space
) if its complement has measure zero. As the space
![]() $\Sigma \times V$
is non-compact, it is natural to study the subset of points of
$\Sigma \times V$
is non-compact, it is natural to study the subset of points of
![]() $\Sigma \times V$
whose future orbit returns infinitely many times to a fixed open bounded set:
$\Sigma \times V$
whose future orbit returns infinitely many times to a fixed open bounded set:
One can be more specific. If
![]() $\mathrm {B}_1,\mathrm {B}_2\subset \Sigma \times W$
, we want to understand the measure of
$\mathrm {B}_1,\mathrm {B}_2\subset \Sigma \times W$
, we want to understand the measure of
To this end, one considers the sum
![]() .
.
Lemma 2.4.3. If
![]() , then
, then
![]() However, if
However, if
![]() $\nu $
has no atoms and f is ergodic with respect to
$\nu $
has no atoms and f is ergodic with respect to
![]() , then
, then
![]() $\mathcal K(f)$
has total mass and for every pair
$\mathcal K(f)$
has total mass and for every pair
![]() $\mathrm {B}_1,\mathrm {B}_2$
, one has
$\mathrm {B}_1,\mathrm {B}_2$
, one has
![]() $\mathcal K(\mathrm {B}_1,\mathrm {B}_2)$
has total mass on
$\mathcal K(\mathrm {B}_1,\mathrm {B}_2)$
has total mass on
![]() $\mathrm {B}_1.$
$\mathrm {B}_1.$
Proof. This is a standard argument valid for any measure-preserving transformation. The first assertion follows by looking at the tail of the series in question:

where, for each
![]() $k\in \mathbb {N}, E_k =\{p\in \mathrm {B}_1:\text { there exists } N\geq k\textrm { with }f^N(p)\in \mathrm {B}_2\}.$
The second assertion can be found in, for example, Aaronson’s book [Reference Aaronson1, p. 22].
$k\in \mathbb {N}, E_k =\{p\in \mathrm {B}_1:\text { there exists } N\geq k\textrm { with }f^N(p)\in \mathrm {B}_2\}.$
The second assertion can be found in, for example, Aaronson’s book [Reference Aaronson1, p. 22].
2.5 An ergodic dichotomy
As in §2.3, let
![]() $\unicode{x3c3} ^r$
be the suspension of the shift on
$\unicode{x3c3} ^r$
be the suspension of the shift on
![]() $\Sigma $
by the function
$\Sigma $
by the function
![]() $r.$
If
$r.$
If
![]() $\nu $
is a
$\nu $
is a
![]() $\sigma $
-invariant probability measure, then
$\sigma $
-invariant probability measure, then
![]() $\nu \otimes \,dt/\int rd\nu $
is invariant under the translation flow
$\nu \otimes \,dt/\int rd\nu $
is invariant under the translation flow
![]() $\Sigma \times \mathbb {R}$
and induces thus a
$\Sigma \times \mathbb {R}$
and induces thus a
![]() $\unicode{x3c3} ^r$
-invariant probability measure on
$\unicode{x3c3} ^r$
-invariant probability measure on
![]() denoted by
denoted by
![]() $\hat \nu .$
$\hat \nu .$
Remark 2.5.1. It is a classical fact, stated for example by Bowen and Ruelle [Reference Bowen and Ruelle16], that if
![]() $\nu $
is the equilibrium state of
$\nu $
is the equilibrium state of
![]() $-h(\unicode{x3c3} ^r)r $
, then
$-h(\unicode{x3c3} ^r)r $
, then
![]() $\hat \nu $
realizes the topological entropy of
$\hat \nu $
realizes the topological entropy of
![]() $\unicode{x3c3} _r.$
$\unicode{x3c3} _r.$
Let
![]() $K:\Sigma \times \mathbb {R} \to V$
be a
$K:\Sigma \times \mathbb {R} \to V$
be a
![]() $\langle\hat r\rangle $
-invariant Hölder-continuous function and consider the flow
$\langle\hat r\rangle $
-invariant Hölder-continuous function and consider the flow

Consider the measure on
defined by
.
Theorem 2.5.2. (Sambarino [Reference Sambarino66, Theorem 3.8])
Assume the group generated by the periods of
![]() $(r,K)$
is dense in
$(r,K)$
is dense in
![]() $\mathbb {R}\times V$
and that
$\mathbb {R}\times V$
and that
![]() $\int Kd\hat \nu =0$
for the equilibrium state
$\int Kd\hat \nu =0$
for the equilibrium state
![]() $\nu $
of
$\nu $
of
![]() $-h(\unicode{x3c3} ^r)r.$
Then there exists
$-h(\unicode{x3c3} ^r)r.$
Then there exists
![]() $\kappa>0$
such that given two compactly supported continuous functions
$\kappa>0$
such that given two compactly supported continuous functions
one has
as
![]() $t\to \infty .$
$t\to \infty .$
We include the main outline of its proof in Appendix B. As it is classical, the above result holds for characteristic functions of open bounded sets whose boundary has measure zero.
Corollary 2.5.3. Under the same assumptions of Theorem 2.5.2, if
![]() $\dim V=1$
, then
$\dim V=1$
, then
![]() $\psi $
is ergodic with respect to
$\psi $
is ergodic with respect to
![]() If
If
![]() $\dim V\geq 3$
, then
$\dim V\geq 3$
, then
![]()
Proof. The skew-product system
![]() $f^{\mathsf {K}}:\Sigma \times V\to \Sigma \times V$
of equation (7), where
$f^{\mathsf {K}}:\Sigma \times V\to \Sigma \times V$
of equation (7), where
![]() ${\mathsf {K}}:\Sigma \to V$
is defined by
${\mathsf {K}}:\Sigma \to V$
is defined by
 $$ \begin{align}{\mathsf{K}}(x)=\int_0^{r(x)}K(x,s)\,ds,\end{align} $$
$$ \begin{align}{\mathsf{K}}(x)=\int_0^{r(x)}K(x,s)\,ds,\end{align} $$
is the first-return map of
![]() $\psi $
to its global section
$\psi $
to its global section
![]() $(\Sigma \times \{0\})/_\sim \,\times \, V.$
Consequently, following the flow-lines until reaching the section, one finds a natural (measurable) bijection between
$(\Sigma \times \{0\})/_\sim \,\times \, V.$
Consequently, following the flow-lines until reaching the section, one finds a natural (measurable) bijection between
![]() $\psi $
-invariant subsets and f-invariant subsets. If
$\psi $
-invariant subsets and f-invariant subsets. If
![]() $\mu $
is a
$\mu $
is a
![]() $\sigma $
-invariant probability measure on
$\sigma $
-invariant probability measure on
![]() $\Sigma ,$
then this bijection preserves the class of invariant-zero-sets between the measures
$\Sigma ,$
then this bijection preserves the class of invariant-zero-sets between the measures
![]() $\hat \mu \otimes \operatorname {\mathrm {Leb}}$
on
$\hat \mu \otimes \operatorname {\mathrm {Leb}}$
on
![]() and
and
![]() $\mu \otimes \operatorname {\mathrm {Leb}}$
on
$\mu \otimes \operatorname {\mathrm {Leb}}$
on
![]() $\Sigma \times V.$
Thus, we can translate ergodicity results from f to the flow
$\Sigma \times V.$
Thus, we can translate ergodicity results from f to the flow
![]() $\psi $
and vice versa.
$\psi $
and vice versa.
The case
![]() $\dim V=1$
is hence settled by Proposition 2.4.2.
$\dim V=1$
is hence settled by Proposition 2.4.2.
For
![]() $\dim V\geq 3$
, one considers an open
$\dim V\geq 3$
, one considers an open
![]() $A\subset \Sigma $
with
$A\subset \Sigma $
with
![]() $\nu (\partial A)=0,$
an open interval
$\nu (\partial A)=0,$
an open interval
![]() $I\subset \mathbb {R}$
with length
$I\subset \mathbb {R}$
with length
![]() $<\min r$
, and
$<\min r$
, and
![]() $B\subset V$
an open ball. Applying Theorem 2.5.2 to
$B\subset V$
an open ball. Applying Theorem 2.5.2 to
gives a positive C such that for large t, one has
Thus, for a fixed
![]() $t_0>0$
, one has that
$t_0>0$
, one has that

If
![]() $\dim V\geq 3$
, then
$\dim V\geq 3$
, then
![]() and Lemma 2.4.3 gives
and Lemma 2.4.3 gives
![]() in particular, the system is not ergodic.
in particular, the system is not ergodic.
Remark 2.5.4. An ergodicity dichotomy for
![]() $f^{\mathsf {K}}$
has been previously established by Guivarc’h [Reference Guivarch’h36, Corollaire 3 on p. 443] under the stronger assumption that
$f^{\mathsf {K}}$
has been previously established by Guivarc’h [Reference Guivarch’h36, Corollaire 3 on p. 443] under the stronger assumption that
![]() ${\mathsf {K}}$
is aperiodic.
${\mathsf {K}}$
is aperiodic.
By means of Markov partitions (Theorem 2.3.2), the above corollary immediately translates to the following. As in the previous section, let X be a compact metric space equipped with a topologically transitive, Hölder-continuous, metric-Anosov flow
![]() $\phi .$
Let
$\phi .$
Let
![]() $F:X\to V$
be Hölder-continuous and consider the flow
$F:X\to V$
be Hölder-continuous and consider the flow
![]() $\Phi =(\Phi _t:X\times V\to X\times V)_{t\in \mathbb {R}}$
$\Phi =(\Phi _t:X\times V\to X\times V)_{t\in \mathbb {R}}$
 $$ \begin{align*}\Phi_t(p,v)=\bigg(\phi_tp,v-\int_0^s F(\phi_sp)\,ds\bigg).\end{align*} $$
$$ \begin{align*}\Phi_t(p,v)=\bigg(\phi_tp,v-\int_0^s F(\phi_sp)\,ds\bigg).\end{align*} $$
It is convenient to call the flow
![]() $\Phi $
by the skew product of
$\Phi $
by the skew product of
![]() $\phi $
by F.
$\phi $
by F.
Corollary 2.5.5. (Dichotomy)
Assume the group spanned by the periods of
![]() $(1,F)$
is dense in
$(1,F)$
is dense in
![]() $\mathbb {R}\times V$
and that
$\mathbb {R}\times V$
and that
![]() $\int Fdm=0$
for the measure of maximal entropy m of
$\int Fdm=0$
for the measure of maximal entropy m of
![]() $\phi .$
Then,
$\phi .$
Then,
![]() $\Phi $
is mixing as in Theorem 2.5.2, moreover
$\Phi $
is mixing as in Theorem 2.5.2, moreover
If
![]() $\dim V\geq 3$
, then
$\dim V\geq 3$
, then
![]() $\mathcal K(\Phi )$
has zero measure.
$\mathcal K(\Phi )$
has zero measure.
Proof. The proof follows from the corresponding results for subshifts and Remark 2.5.1 describing the measure of maximal entropy of
![]() $\phi .$
$\phi .$
2.6 The critical hypersurface
We recall here two results of Babillot and Ledrappier [Reference Babillot and Ledrappier5]. Their paper concerns differentiable Anosov flows but, as one checks the proofs, only the existence of a Markov coding is required for both their results below. We take the liberty to state them in our broader generality and refer the reader to loc. cit. whose proofs work verbatim.
As before, let
![]() $F:X\to V$
be Hölder-continuous.
$F:X\to V$
be Hölder-continuous.
Assumption A. We will assume throughout the remainder of §2 that the closed group
![]() $\Delta $
spanned by the periods of F has rank
$\Delta $
spanned by the periods of F has rank
![]() $\dim V,$
(that is,
$\dim V,$
(that is,
![]() $\Delta \simeq \mathbb {R}^k\times \mathbb {Z}^{\dim V-k}$
for some
$\Delta \simeq \mathbb {R}^k\times \mathbb {Z}^{\dim V-k}$
for some
![]() ) and that, moreover, the group spanned by
) and that, moreover, the group spanned by
 $$ \begin{align*}\bigg\{(p(\tau),\int_\tau F):\tau\textrm{ periodic}\bigg\}\end{align*} $$
$$ \begin{align*}\bigg\{(p(\tau),\int_\tau F):\tau\textrm{ periodic}\bigg\}\end{align*} $$
is isomorphic to
![]() $\mathbb {R}\times \Delta .$
$\mathbb {R}\times \Delta .$
The compact convex subset of V,
 $$ \begin{align*} \mathcal M^\phi(F)=\bigg\{\int_XFd\mu:\mu\in\mathcal M^\phi\bigg\},\end{align*} $$
$$ \begin{align*} \mathcal M^\phi(F)=\bigg\{\int_XFd\mu:\mu\in\mathcal M^\phi\bigg\},\end{align*} $$
has hence non-empty interior. Also, for each
![]() $\varphi \in V^*$
, one can consider the pressure of the function
$\varphi \in V^*$
, one can consider the pressure of the function
![]() $\varphi (F):X\to \mathbb {R}$
:
$\varphi (F):X\to \mathbb {R}$
:
By Assumption A, the function
![]() $\mathbf {P}:V^*\to \mathbb {R}$
is analytic and strictly convex (Proposition 2.2.5). Using the formula for the derivative of pressure (Proposition 2.2.5), and the natural identification
$\mathbf {P}:V^*\to \mathbb {R}$
is analytic and strictly convex (Proposition 2.2.5). Using the formula for the derivative of pressure (Proposition 2.2.5), and the natural identification
![]() $\operatorname {\mathrm {Gr}}_{\dim V-1}(V^*)\to \mathbb {P}(V),$
one has, for
$\operatorname {\mathrm {Gr}}_{\dim V-1}(V^*)\to \mathbb {P}(V),$
one has, for
![]() $\varphi \in V^*$
, that
$\varphi \in V^*$
, that
where
![]() $m_{-\varphi (F)}$
is the equilibrium state of
$m_{-\varphi (F)}$
is the equilibrium state of
![]() $-\varphi (F).$
One has the following proposition.
$-\varphi (F).$
One has the following proposition.
Proposition 2.6.1. (Babillot and Ledrappier [Reference Babillot and Ledrappier5, Proposition 1.1])
The map
![]() $\wp :V^*\to V$
defined by
$\wp :V^*\to V$
defined by
![]() $\varphi \mapsto d_\varphi \mathbf {P}$
is a diffeomorphism between
$\varphi \mapsto d_\varphi \mathbf {P}$
is a diffeomorphism between
![]() $V^*$
and the interior of
$V^*$
and the interior of
![]() $\mathcal M^\phi (F).$
$\mathcal M^\phi (F).$
Let us denote by
![]() $\mathscr L_F=\mathbb {R}_+\cdot \mathcal M^\varphi (F)$
the closed cone generated by the periods of
$\mathscr L_F=\mathbb {R}_+\cdot \mathcal M^\varphi (F)$
the closed cone generated by the periods of
![]() $F.$
If
$F.$
If
![]() $0$
does not belong to
$0$
does not belong to
![]() $\mathcal M^\phi (F)$
, then
$\mathcal M^\phi (F)$
, then
![]() $\mathscr L_F$
is a sharp cone (that is, does not contain a hyperplane of V) and its interior is
$\mathscr L_F$
is a sharp cone (that is, does not contain a hyperplane of V) and its interior is
One has moreover the following proposition.
Proposition 2.6.2. (Babillot and Ledrappier [Reference Babillot and Ledrappier5, Proposition 3.1])
Assume
![]() $0\notin \mathcal M^\phi (F).$
Then the set
$0\notin \mathcal M^\phi (F).$
Then the set
![]() $\wp (\{\varphi \in V^*:\mathbf {P}(\varphi )=0\})$
generates the cone
$\wp (\{\varphi \in V^*:\mathbf {P}(\varphi )=0\})$
generates the cone
![]() $\operatorname {\mathrm {int}}\mathscr L_F.$
$\operatorname {\mathrm {int}}\mathscr L_F.$
Remark 2.6.3. Observe that if
![]() $\varphi \in V^*$
is such that
$\varphi \in V^*$
is such that
![]() $\sum _{\tau \textrm { periodic}}e^{-\ell _\tau (\varphi \circ F)}<\infty $
, then necessarily
$\sum _{\tau \textrm { periodic}}e^{-\ell _\tau (\varphi \circ F)}<\infty $
, then necessarily
![]() $\varphi $
is strictly positive on the cone
$\varphi $
is strictly positive on the cone
![]() $\mathscr L_F,$
that is,
$\mathscr L_F,$
that is,
![]() $\varphi \in \operatorname {\mathrm {int}}(\mathscr L_F^*).$
Indeed, if
$\varphi \in \operatorname {\mathrm {int}}(\mathscr L_F^*).$
Indeed, if
![]() $\sum _{\tau }e^{-\ell _\tau (\varphi \circ F)}$
is convergent, then the formula for pressure on Proposition 2.2.5 gives that
$\sum _{\tau }e^{-\ell _\tau (\varphi \circ F)}$
is convergent, then the formula for pressure on Proposition 2.2.5 gives that
![]() $\mathbf {P}(\varphi )\leq 0.$
Since
$\mathbf {P}(\varphi )\leq 0.$
Since
![]() $\mathbf {P}(0)>0$
, there exists
$\mathbf {P}(0)>0$
, there exists
![]() $s\in (0,1]$
such that
$s\in (0,1]$
such that
![]() $\mathbf {P}(s\varphi )=0.$
The variational principle (equation (2)) implies that
$\mathbf {P}(s\varphi )=0.$
The variational principle (equation (2)) implies that
for every periodic orbit
![]() $\tau ,$
and thus Lemma 2.2.7 applies to give that
$\tau ,$
and thus Lemma 2.2.7 applies to give that
![]() $\varphi (F)$
is Livšic-cohomologous to a strictly positive function and
$\varphi (F)$
is Livšic-cohomologous to a strictly positive function and
![]() $\mathscr h_{\varphi (F)}\in (0,1].$
$\mathscr h_{\varphi (F)}\in (0,1].$
We are thus interested in the convergence domain of F
 $$ \begin{align*}\mathcal D_F & =\{\varphi\in\operatorname{\mathrm{int}}(\mathscr L_F^*): \mathscr h_{\varphi(F)}\in(0,1)\}\\ & \subset \bigg\{\varphi\in V^*: \sum_{\tau\textrm{ periodic}} e^{-\ell_\tau(\varphi\circ F)}<\infty\bigg\}, \end{align*} $$
$$ \begin{align*}\mathcal D_F & =\{\varphi\in\operatorname{\mathrm{int}}(\mathscr L_F^*): \mathscr h_{\varphi(F)}\in(0,1)\}\\ & \subset \bigg\{\varphi\in V^*: \sum_{\tau\textrm{ periodic}} e^{-\ell_\tau(\varphi\circ F)}<\infty\bigg\}, \end{align*} $$
and the critical hypersurface (also usually called the entropy-one set or the Manhattan curve)
whose name is justified in the next corollary.
Corollary 2.6.4. Assume
![]() $0\notin \mathcal M^\phi (F).$
Then
$0\notin \mathcal M^\phi (F).$
Then
![]() $\mathcal D_F=\mathbf {P}^{-1}(-\infty ,0)$
and
$\mathcal D_F=\mathbf {P}^{-1}(-\infty ,0)$
and
![]() $\mathcal Q_F=\mathbf {P}^{-1}(0)$
. Consequently,
$\mathcal Q_F=\mathbf {P}^{-1}(0)$
. Consequently,
![]() $\mathcal D_F$
is a strictly convex set whose boundary coincides with
$\mathcal D_F$
is a strictly convex set whose boundary coincides with
![]() $\mathcal Q_F.$
The latter is a closed analytic co-dimension-one submanifold of
$\mathcal Q_F.$
The latter is a closed analytic co-dimension-one submanifold of
![]() $V^*.$
The map
$V^*.$
The map
induces a diffeomorphism between
![]() $\mathcal Q_F$
and directions in the interior of the cone
$\mathcal Q_F$
and directions in the interior of the cone
![]() $\mathscr L_F.$
$\mathscr L_F.$
Proof. We have already shown the inclusions
![]() $\mathbf {P}^{-1}(-\infty ,0)\subset \mathcal D_F$
and
$\mathbf {P}^{-1}(-\infty ,0)\subset \mathcal D_F$
and
![]() $\mathbf {P}^{-1}(0)\subset \mathcal Q_F.$
The other ones follow at once from Lemmas 2.2.7 and 2.1.1. Since
$\mathbf {P}^{-1}(0)\subset \mathcal Q_F.$
The other ones follow at once from Lemmas 2.2.7 and 2.1.1. Since
![]() $0\notin \mathcal M^\varphi (F)$
, Proposition 2.6.1 implies that
$0\notin \mathcal M^\varphi (F)$
, Proposition 2.6.1 implies that
![]() $\mathbf {P}$
has no critical points, thus
$\mathbf {P}$
has no critical points, thus
![]() $\mathbf {P}^{-1}(0)=\mathcal Q_F$
is an analytic sub-manifold of
$\mathbf {P}^{-1}(0)=\mathcal Q_F$
is an analytic sub-manifold of
![]() $V^*.$
Strict convexity follows from that of
$V^*.$
Strict convexity follows from that of
![]() $\mathbf {P},$
and the last assertion follows by observing that the tangent space
$\mathbf {P},$
and the last assertion follows by observing that the tangent space
![]() ${\mathsf {T}}_\varphi \mathcal Q_F$
equals
${\mathsf {T}}_\varphi \mathcal Q_F$
equals
![]() $\ker d_\varphi \mathbf {P}.$
$\ker d_\varphi \mathbf {P}.$
We now focus on the variation of the critical hypersurface when F varies. To this end, consider the Banach space
![]() $\operatorname {\mathrm {Holder}}^\alpha (X,V)$
of V-valued Hölder continuous functions with exponent
$\operatorname {\mathrm {Holder}}^\alpha (X,V)$
of V-valued Hölder continuous functions with exponent
![]() $\alpha .$
The pressure can be considered as an analytic map
$\alpha .$
The pressure can be considered as an analytic map
![]() $\mathbf {P}:\operatorname {\mathrm {Holder}}^\alpha (X,V)\times V^*\to \mathbb {R}$
defined as
$\mathbf {P}:\operatorname {\mathrm {Holder}}^\alpha (X,V)\times V^*\to \mathbb {R}$
defined as
![]() $\mathbf {P}(G,\psi ):=P(\phi ,-\psi (G)).$
Its differential at the point
$\mathbf {P}(G,\psi ):=P(\phi ,-\psi (G)).$
Its differential at the point
![]() $(F,\varphi )$
on the vector
$(F,\varphi )$
on the vector
![]() $(G,\psi )$
is
$(G,\psi )$
is
and vanishes identically only if
![]() $(F,\varphi )=(0,0).$
The pre-image
$(F,\varphi )=(0,0).$
The pre-image
![]() $\mathbf {P}^{-1}(0)$
is thus a Banach-manifold.
$\mathbf {P}^{-1}(0)$
is thus a Banach-manifold.
If
![]() $F\in \operatorname {\mathrm {Holder}}^\alpha (X,V)$
is such that
$F\in \operatorname {\mathrm {Holder}}^\alpha (X,V)$
is such that
![]() $0\notin \mathcal M^\phi (F),$
then its critical hypersurface
$0\notin \mathcal M^\phi (F),$
then its critical hypersurface
is the intersection of
![]() $\{F\}\times V^*$
with the level set
$\{F\}\times V^*$
with the level set
![]() $\mathbf {P}^{-1}(0).$
This intersection will vary analytically on compact sets with F as long as the tangent space
$\mathbf {P}^{-1}(0).$
This intersection will vary analytically on compact sets with F as long as the tangent space
![]() $\ker d_{(F,\varphi )}\mathbf {P}$
(for fixed
$\ker d_{(F,\varphi )}\mathbf {P}$
(for fixed
![]() $(F,\varphi )$
with
$(F,\varphi )$
with
![]() $\mathbf {P}(F,\varphi )=0$
) is transverse to the vector space
$\mathbf {P}(F,\varphi )=0$
) is transverse to the vector space
![]() $\{0\}\times V^*.$
Since
$\{0\}\times V^*.$
Since
![]() $\ker d_{(F,\varphi )}\mathbf {P}$
has co-dimension 1, transversality is implied by
$\ker d_{(F,\varphi )}\mathbf {P}$
has co-dimension 1, transversality is implied by
![]() $\ker d_{(F,\varphi )}\mathbf {P}\cap \{0\}\times V^*$
being co-dimension
$\ker d_{(F,\varphi )}\mathbf {P}\cap \{0\}\times V^*$
being co-dimension
![]() $1$
on
$1$
on
![]() $V^*.$
However, by Corollary 2.6.4, this latter intersection is, as long as F verifies assumption A and
$V^*.$
However, by Corollary 2.6.4, this latter intersection is, as long as F verifies assumption A and
![]() $0\notin \mathcal M^\phi (F),$
the tangent space
$0\notin \mathcal M^\phi (F),$
the tangent space
![]() ${\mathsf {T}}_\varphi \mathcal Q_F,$
which has co-dimension
${\mathsf {T}}_\varphi \mathcal Q_F,$
which has co-dimension
![]() $1.$
We have thus established the following corollary.
$1.$
We have thus established the following corollary.
Corollary 2.6.5. The critical hypersurface
![]() $\mathcal Q_F$
varies analytically on compact sets when varying the function F among Hölder functions verifying the hypothesis of Corollary 2.6.4.
$\mathcal Q_F$
varies analytically on compact sets when varying the function F among Hölder functions verifying the hypothesis of Corollary 2.6.4.
2.7 Dynamical intersection and the critical hypersurface
We recall here the concept of dynamical intersection of Bridgeman et al [Reference Bridgeman, Canary, Labourie and Sambarino17]. Similar concepts have been previously studied by Bonahon [Reference Bonahon11], Burger [Reference Burger19], Croke and Fathi [Reference Croke and Fathi28], and Knieper [Reference Knieper42], among others.
Let
![]() $f:X\to \mathbb {R}_+$
be a positive Hölder-continuous function and, for
$f:X\to \mathbb {R}_+$
be a positive Hölder-continuous function and, for
![]() $t>0,$
consider the finite set
$t>0,$
consider the finite set
![]() ${\mathsf {R}}_t(f)=\{\tau \textrm { periodic}:\ell _\tau (f)\leq t\}.$
Let
${\mathsf {R}}_t(f)=\{\tau \textrm { periodic}:\ell _\tau (f)\leq t\}.$
Let
![]() $g:X\to \mathbb {R}$
be Hölder-continuous (but not necessarily positive). Then the dynamical intersection between f and g is defined by
$g:X\to \mathbb {R}$
be Hölder-continuous (but not necessarily positive). Then the dynamical intersection between f and g is defined by
 $$ \begin{align*}\mathbf{I}(f,g)=\lim_{t\to\infty}\frac1{\#{\mathsf{R}}_t(f)}\sum_{\tau\in {\mathsf{R}}_t(f)}\frac{\ell_\tau(g)}{\ell_\tau(f)}.\end{align*} $$
$$ \begin{align*}\mathbf{I}(f,g)=\lim_{t\to\infty}\frac1{\#{\mathsf{R}}_t(f)}\sum_{\tau\in {\mathsf{R}}_t(f)}\frac{\ell_\tau(g)}{\ell_\tau(f)}.\end{align*} $$
Then one has the following proposition.
Proposition 2.7.1. [Reference Bridgeman, Canary, Labourie and Sambarino17, §3.4]
One has
 $$ \begin{align*}\mathbf{I}(f,g)=\frac{\int gdm_{-\mathscr h_ff}}{\int f\,dm_{-\mathscr h_ff}},\end{align*} $$
$$ \begin{align*}\mathbf{I}(f,g)=\frac{\int gdm_{-\mathscr h_ff}}{\int f\,dm_{-\mathscr h_ff}},\end{align*} $$
in particular,
![]() $\mathbf {I}$
is well defined and varies analytically with f and g among Hölder- continuous functions with fixed Hölder exponent. If g is moreover positive, then one has
$\mathbf {I}$
is well defined and varies analytically with f and g among Hölder- continuous functions with fixed Hölder exponent. If g is moreover positive, then one has
![]() $\mathbf {I}(f,g)\geq \mathscr h_f/\mathscr h_g.$
$\mathbf {I}(f,g)\geq \mathscr h_f/\mathscr h_g.$
We now place ourselves in the context of the previous subsection, that is, we consider a Hölder-continuous
![]() $F:X\to V$
and we assume moreover that
$F:X\to V$
and we assume moreover that
![]() $0\notin \mathcal M^\phi (F).$
For
$0\notin \mathcal M^\phi (F).$
For
![]() $\varphi \in \mathcal Q_F$
, we consider the map
$\varphi \in \mathcal Q_F$
, we consider the map
![]() $\mathbf {I}_{\varphi }:V^*\to \mathbb {R}$
defined by
$\mathbf {I}_{\varphi }:V^*\to \mathbb {R}$
defined by
 $$ \begin{align}\mathbf{I}_{\varphi}(\psi):= \mathbf{I}(\varphi(F),\psi(F))=\frac{\int \psi(F)\,dm_{-\varphi(F)}}{\int\varphi(F)\,dm_{-\varphi(F)}},\end{align} $$
$$ \begin{align}\mathbf{I}_{\varphi}(\psi):= \mathbf{I}(\varphi(F),\psi(F))=\frac{\int \psi(F)\,dm_{-\varphi(F)}}{\int\varphi(F)\,dm_{-\varphi(F)}},\end{align} $$
where the last equality comes from Proposition 2.7.1 and the fact that
![]() $\mathscr h_{\varphi (F)}=1$
. Observe that it is a linear map. We then have the following explicit interpretation of the tangent space to the critical hypersurface purely in terms of periods.
$\mathscr h_{\varphi (F)}=1$
. Observe that it is a linear map. We then have the following explicit interpretation of the tangent space to the critical hypersurface purely in terms of periods.
Corollary 2.7.2. Let
![]() $F:X\to V$
be as in §2.6 and such that
$F:X\to V$
be as in §2.6 and such that
![]() $0\notin \mathcal M^\phi (F).$
Then for
$0\notin \mathcal M^\phi (F).$
Then for
![]() $\varphi \in \mathcal Q_F$
, one has
$\varphi \in \mathcal Q_F$
, one has
![]() ${\mathsf {T}}_\varphi \mathcal Q_F=\ker \mathbf {I}_\varphi .$
${\mathsf {T}}_\varphi \mathcal Q_F=\ker \mathbf {I}_\varphi .$
3 A Ledrappier correspondence
In [Reference Ledrappier44], Ledrappier establishes, for a closed negatively curved manifold
![]() $M,$
bijections between Livšic-cohomology classes of pressure zero functions on
$M,$
bijections between Livšic-cohomology classes of pressure zero functions on
![]() ${\mathsf {T}}^1M,$
normalized Hölder cocycles for the action of
${\mathsf {T}}^1M,$
normalized Hölder cocycles for the action of
![]() $\pi _1M$
on the visual boundary
$\pi _1M$
on the visual boundary
![]() $\partial _\infty \tilde M$
of the universal cover of
$\partial _\infty \tilde M$
of the universal cover of
![]() $M,$
quasi-invariant measures on
$M,$
quasi-invariant measures on
![]() $\partial _\infty \tilde M$
, among other objects. The purpose of this section is to establish, in the context of word-hyperbolic groups with metric-Anosov geodesic flow, some of these correspondences. We also extend results of Sambarino [Reference Sambarino64–Reference Sambarino66] to this setting. Some ideas of Bridgeman et al [Reference Bridgeman, Canary, Labourie and Sambarino17, Reference Bridgeman, Canary, Labourie and Sambarino18] and Carvajales [Reference Carvajales23, Appendix] are used. The reader can also check the work of Paulin, Pollicott, and Schapira [Reference Paulin, Pollicott and Schapira54] for similar results in situations allowing cusps.
$\partial _\infty \tilde M$
, among other objects. The purpose of this section is to establish, in the context of word-hyperbolic groups with metric-Anosov geodesic flow, some of these correspondences. We also extend results of Sambarino [Reference Sambarino64–Reference Sambarino66] to this setting. Some ideas of Bridgeman et al [Reference Bridgeman, Canary, Labourie and Sambarino17, Reference Bridgeman, Canary, Labourie and Sambarino18] and Carvajales [Reference Carvajales23, Appendix] are used. The reader can also check the work of Paulin, Pollicott, and Schapira [Reference Paulin, Pollicott and Schapira54] for similar results in situations allowing cusps.
Let
be a finitely generated, non-elementary, word-hyperbolic group (see [Reference Ghys and de la Harpe30] for a definition). Denote by
the Gromov–Mineyev geodesic flow of
(see [Reference Gromov33] and [Reference Mineyev51]). The total space
is the quotient of
by a properly discontinuous co-compact
-action (defined in loc. cit.). This action restricted to
coincides with the induced
-action on its Gromov boundary, and commutes with the
![]() $\mathbb {R}$
-action by translations, giving on the quotient the desired flow
$\mathbb {R}$
-action by translations, giving on the quotient the desired flow
![]() ${\mathsf {g}}.$
We will save the notation
${\mathsf {g}}.$
We will save the notation
for the pair consisting on the space
equipped with the above
-action.
Assumption B. We will assume throughout §3 that
![]() ${\mathsf {g}}$
is metric-Anosov (recall that, in general,
${\mathsf {g}}$
is metric-Anosov (recall that, in general,
![]() ${\mathsf {g}}$
is transitive (see Remark 3.0.1)) and that the lamination induced on the quotient by
${\mathsf {g}}$
is transitive (see Remark 3.0.1)) and that the lamination induced on the quotient by
![]() is the central-unstable lamination of
is the central-unstable lamination of
![]() ${\mathsf {g}}.$
${\mathsf {g}}.$
Let us emphasize that, in what follows, the Gromov–Mineyev geodesic flow is merely an auxiliary object. The whole discussion works verbatim replacing
![]() ${\mathsf {g}}$
by the following flows known to satisfy Assumption B:
${\mathsf {g}}$
by the following flows known to satisfy Assumption B:
-
• the non-wandering set of the geodesic flow of a convex co-compact action of
 on a
on a
 $\mathrm {CAT}(-1)$
space (if this is known to exist), see [Reference Constantine, Lafont and Thompson27];
$\mathrm {CAT}(-1)$
space (if this is known to exist), see [Reference Constantine, Lafont and Thompson27]; -
• the geodesic flow of a projective-Anosov representation of
 $\rho $
(again if this is known to exist) as introduced by Bridgeman et al [Reference Bridgeman, Canary, Labourie and Sambarino17], see also §5.1.
$\rho $
(again if this is known to exist) as introduced by Bridgeman et al [Reference Bridgeman, Canary, Labourie and Sambarino17], see also §5.1.
Recall that every hyperbolic element (that is, an infinite order element)
![]() has two fixed points on
has two fixed points on
![]() the attracting
the attracting
![]() $\gamma _+$
and the repelling
$\gamma _+$
and the repelling
![]() $\gamma _-.$
If
$\gamma _-.$
If
![]() , then
, then
![]() $\gamma ^nx\to \gamma _+$
as
$\gamma ^nx\to \gamma _+$
as
![]() $n\to \infty .$
The axis
$n\to \infty .$
The axis
![]() $(\gamma _-,\gamma _+)\times \mathbb {R}$
projects then to a periodic orbit of
$(\gamma _-,\gamma _+)\times \mathbb {R}$
projects then to a periodic orbit of
![]() ${\mathsf {g}},$
denoted by
${\mathsf {g}},$
denoted by
![]() $[\gamma ].$
If
$[\gamma ].$
If
![]() $l(\gamma )$
denotes the translation length of
$l(\gamma )$
denotes the translation length of
![]() $\gamma $
along this axis, then
$\gamma $
along this axis, then
![]() $l(\gamma )$
is an integer multiple of the period of the periodic orbit
$l(\gamma )$
is an integer multiple of the period of the periodic orbit
![]() $[\gamma ].$
Observe that we allow
$[\gamma ].$
Observe that we allow
![]() $[\gamma ]$
to tour several times along the orbits it surjects to, so at least formally, we let
$[\gamma ]$
to tour several times along the orbits it surjects to, so at least formally, we let
![]() $[\gamma ^n]$
be the orbit
$[\gamma ^n]$
be the orbit
![]() $[\gamma ]$
toured n-times.
$[\gamma ]$
toured n-times.
Remark 3.0.1. We briefly justify why
![]() ${\mathsf {g}}$
is transitive. It suffices to show that given two open sets
${\mathsf {g}}$
is transitive. It suffices to show that given two open sets
![]() $U, V$
, there exists
$U, V$
, there exists
![]() $t\in \mathbb {R}$
such that
$t\in \mathbb {R}$
such that
![]() ${\mathsf {g}}_t(U)\cap V\neq \emptyset ,$
so the question is reduced to the same question for the action of
${\mathsf {g}}_t(U)\cap V\neq \emptyset ,$
so the question is reduced to the same question for the action of
![]() on
on
![]() ; the open sets to be considered can be reduced to be of the form
; the open sets to be considered can be reduced to be of the form
![]() $U_1\times U_2$
and
$U_1\times U_2$
and
![]() $V_1\times V_2,$
where
$V_1\times V_2,$
where
![]() are open and
are open and
![]() $\overline {U_1}\cap U_2=\overline {V_1}\cap V_2=\emptyset ;$
an element
$\overline {U_1}\cap U_2=\overline {V_1}\cap V_2=\emptyset ;$
an element
![]() with
with
![]() $\gamma _-\in U_2$
and
$\gamma _-\in U_2$
and
![]() $\gamma _+\in V_1$
has a positive power such that
$\gamma _+\in V_1$
has a positive power such that
![]() $\gamma ^n(U_1\times U_2)\cap V_1\times V_2\neq \emptyset .$
$\gamma ^n(U_1\times U_2)\cap V_1\times V_2\neq \emptyset .$
3.1 The Ledrappier potential of a Hölder cocycle
Let V be a finite dimensional real vector space. A Hölder cocycle is a function
![]() such that:
such that:
-
• for all
 , one has
, one has
 $c(\gamma h,(x,y))=c(h,(x,y))+c(\gamma ,h(x,y));$
$c(\gamma h,(x,y))=c(h,(x,y))+c(\gamma ,h(x,y));$
-
• there exists
 $\alpha \in (0,1]$
such that for every
$\alpha \in (0,1]$
such that for every
 , the map
, the map
 $c(\gamma ,\cdot )$
is
$c(\gamma ,\cdot )$
is
 $\alpha $
-Hölder continuous.
$\alpha $
-Hölder continuous.
The period of a Hölder cocycle for a hyperbolic
![]() is
is
![]() $\ell _c(\gamma ):=c(\gamma ,(\gamma ^-,\gamma ^+)).$
Two cocycles
$\ell _c(\gamma ):=c(\gamma ,(\gamma ^-,\gamma ^+)).$
Two cocycles
![]() $c,c'$
are cohomologous if there exists a Hölder-continuous function
$c,c'$
are cohomologous if there exists a Hölder-continuous function
![]() such that for all
such that for all
![]() and
and
![]() , one has
, one has
Two cohomologous cocycles have the same marked spectrum
![]() $\gamma \mapsto \ell _c(\gamma ).$
The following should be compared with [Reference Ledrappier44, Théorème 3].
$\gamma \mapsto \ell _c(\gamma ).$
The following should be compared with [Reference Ledrappier44, Théorème 3].
Proposition 3.1.1. For every Hölder cocycle c, there exists a Hölder-continuous function
![]() such that for every hyperbolic
such that for every hyperbolic
![]() , one has
, one has
 $$ \begin{align*}\int_{[\gamma]}\mathcal J_c=\ell_c(\gamma).\end{align*} $$
$$ \begin{align*}\int_{[\gamma]}\mathcal J_c=\ell_c(\gamma).\end{align*} $$
Cohomologous cocycles induce Livšic-cohomolgous functions.
Proof. The general case follows from the case
![]() $V=\mathbb {R}$
by the Riesz representation theorem. Assume thus
$V=\mathbb {R}$
by the Riesz representation theorem. Assume thus
![]() $V=\mathbb {R}$
and consider the trivial line bundle
$V=\mathbb {R}$
and consider the trivial line bundle
![]() equipped with the bundle automorphisms
equipped with the bundle automorphisms
where
![]() $p=(x,y,t).$
Denote by
$p=(x,y,t).$
Denote by
![]() the quotient line bundle. It is equipped with a flow
the quotient line bundle. It is equipped with a flow
![]() $(\hat {\mathsf {g}}_t:{\mathsf {F}}\to {\mathsf {F}})_{t\in \mathbb {R}}$
by bundle automorphisms, induced on the quotient by
$(\hat {\mathsf {g}}_t:{\mathsf {F}}\to {\mathsf {F}})_{t\in \mathbb {R}}$
by bundle automorphisms, induced on the quotient by
Let
![]() $|\,|$
be a Euclidean metric on
$|\,|$
be a Euclidean metric on
![]() ${\mathsf {F}}$
and define, for
${\mathsf {F}}$
and define, for
![]() $v\in {\mathsf {F}}_p,$
$v\in {\mathsf {F}}_p,$
It is a translation cocycle over
![]() ${\mathsf {g}},$
indeed since
${\mathsf {g}},$
indeed since
![]() ${\mathsf {F}}_p$
is one dimensional, the choice of v does not matter, and since
${\mathsf {F}}_p$
is one dimensional, the choice of v does not matter, and since
![]() $\hat {\mathsf {g}}$
is a flow, one has
$\hat {\mathsf {g}}$
is a flow, one has
 $$ \begin{align*}\log\frac{|\hat{\mathsf{ g}}_{t+s}(v)|}{|v|}= \log\frac{|\hat{\mathsf{g}}_{t}(\hat{\mathsf{g}}_sv)|}{|v|}\frac{|\hat{\mathsf{g}}_s(v)|}{|\hat{\mathsf{g}}_s(v)|}=\log\frac{|\hat{\mathsf{g}}_{t}(\hat{\mathsf{g}}_sv)|}{|\hat{\mathsf{g}}_s(v)|}+\log\frac{|\hat{\mathsf{ g}}_s(v)|}{|v|}.\end{align*} $$
$$ \begin{align*}\log\frac{|\hat{\mathsf{ g}}_{t+s}(v)|}{|v|}= \log\frac{|\hat{\mathsf{g}}_{t}(\hat{\mathsf{g}}_sv)|}{|v|}\frac{|\hat{\mathsf{g}}_s(v)|}{|\hat{\mathsf{g}}_s(v)|}=\log\frac{|\hat{\mathsf{g}}_{t}(\hat{\mathsf{g}}_sv)|}{|\hat{\mathsf{g}}_s(v)|}+\log\frac{|\hat{\mathsf{ g}}_s(v)|}{|v|}.\end{align*} $$
By Corollary 2.2.3, there exists a Hölder-continuous function
![]() such that
such that
![]() $\mathcal T$
and
$\mathcal T$
and
![]() $k_{\mathcal J_c}$
are Livšic-cohomologous. We end the proof by a period computation. For every hyperbolic
$k_{\mathcal J_c}$
are Livšic-cohomologous. We end the proof by a period computation. For every hyperbolic
![]() , one has, for all
, one has, for all
![]() $s\in \mathbb {R},$
that
$s\in \mathbb {R},$
that
![]() $\gamma (\gamma _-,\gamma _+,s)=(\gamma _-,\gamma _+,e^{-\ell _c(\gamma )}s),$
or equivalently, for any
$\gamma (\gamma _-,\gamma _+,s)=(\gamma _-,\gamma _+,e^{-\ell _c(\gamma )}s),$
or equivalently, for any
![]() and
and
![]() $v\in {\mathsf {F}}_x,$
$v\in {\mathsf {F}}_x,$
 $$ \begin{align*}\ell_c(\gamma)=\log\frac{|\hat{\mathsf{ g}}_{p(\gamma)}v|}{|v|}=\ell_{[\gamma]}(\mathcal T)=\int_{[\gamma]}\mathcal J_c,\end{align*} $$
$$ \begin{align*}\ell_c(\gamma)=\log\frac{|\hat{\mathsf{ g}}_{p(\gamma)}v|}{|v|}=\ell_{[\gamma]}(\mathcal T)=\int_{[\gamma]}\mathcal J_c,\end{align*} $$
where
![]() $p(\gamma )$
is the period of
$p(\gamma )$
is the period of
![]() $[\gamma ]$
for
$[\gamma ]$
for
![]() ${\mathsf {g}}.$
Since cohomologous cocycles have the same marked spectrum, the associated functions have the same periods and are thus Livšic-cohomolgous by Theorem 2.2.2.
${\mathsf {g}}.$
Since cohomologous cocycles have the same marked spectrum, the associated functions have the same periods and are thus Livšic-cohomolgous by Theorem 2.2.2.
Definition 3.1.2. We say that
![]() $\mathcal J_c$
is a Ledrappier potential of c over
$\mathcal J_c$
is a Ledrappier potential of c over
![]() ${\mathsf {g}}.$
${\mathsf {g}}.$
3.2 Real cocycles and reparameterizations
Assume now
![]() $V=\mathbb {R}$
and consider a cocycle c with non-negative (and not all vanishing) periods. Define its entropy by
$V=\mathbb {R}$
and consider a cocycle c with non-negative (and not all vanishing) periods. Define its entropy by
For such a cocycle, consider the action of
![]() on
on
![]() via c:
via c:
Let us denote by
![]() ${\unicode{x3c7} ^{c}}$
the quotient space
${\unicode{x3c7} ^{c}}$
the quotient space
![]() The following is reported by Sambarino [Reference Sambarino65] for fundamental groups of closed negatively curved manifolds and by Carvajales [Reference Carvajales23] for the refraction cocycle of a
The following is reported by Sambarino [Reference Sambarino65] for fundamental groups of closed negatively curved manifolds and by Carvajales [Reference Carvajales23] for the refraction cocycle of a
![]() ${{{\Delta }}}$
-Anosov representation (see Definition 5.3.1).
${{{\Delta }}}$
-Anosov representation (see Definition 5.3.1).
Theorem 3.2.2. If c is a Hölder cocycle with non-negative periods and finite entropy, then its Ledrappier potential is Livšic-cohomologous to a strictly positive function. Moreover, the above action of
![]() on
on
![]() is properly discontinuous and co-compact, and the flow
is properly discontinuous and co-compact, and the flow
![]() $\phi ^c=(\phi ^c_t:{\unicode{x3c7} ^{c}}\to {\unicode{x3c7} ^{c}})_{t\in \mathbb {R}}$
induced on the quotient by the
$\phi ^c=(\phi ^c_t:{\unicode{x3c7} ^{c}}\to {\unicode{x3c7} ^{c}})_{t\in \mathbb {R}}$
induced on the quotient by the
![]() $\mathbb {R}$
-translation flow is Hölder-conjugated to the reparameterization of
$\mathbb {R}$
-translation flow is Hölder-conjugated to the reparameterization of
![]() ${\mathsf {g}}$
by
${\mathsf {g}}$
by
![]() $\mathcal J_c.$
$\mathcal J_c.$
The topological entropy of
![]() $\phi ^c$
is thus
$\phi ^c$
is thus
![]() $\mathscr h_c.$
(When
$\mathscr h_c.$
(When
![]() has torsion elements, this fact requires some work, see the work of Carvajales et al [Reference Carvajales, Dai, Pozzetti and Wienhard24, §5] for details.)
has torsion elements, this fact requires some work, see the work of Carvajales et al [Reference Carvajales, Dai, Pozzetti and Wienhard24, §5] for details.)
Proof. The first assertion follows at once from Lemma 2.2.7. For the remaining statements, we continue as in the proof of the proposition but for the cocycle
![]() $-c.$
Observe first that
$-c.$
Observe first that
![]() $-\mathcal J_c=\mathcal J_{-c}.$
Since
$-\mathcal J_c=\mathcal J_{-c}.$
Since
![]() $\mathcal T$
and
$\mathcal T$
and
![]() $k_{\mathcal J_{-c}}$
are Livšic-cohomologous, there exists
$k_{\mathcal J_{-c}}$
are Livšic-cohomologous, there exists
![]() such that for all
such that for all
![]() , and
, and
![]() $v\in {\mathsf {F}}_p$
, one has (recall equation (11))
$v\in {\mathsf {F}}_p$
, one has (recall equation (11))
 $$ \begin{align*}\log\frac{|\hat{\mathsf{ g}}_tv|}{|v|}-\int_0^t\mathcal J_{-c}=U({\mathsf{g}}_tp)-U(x).\end{align*} $$
$$ \begin{align*}\log\frac{|\hat{\mathsf{ g}}_tv|}{|v|}-\int_0^t\mathcal J_{-c}=U({\mathsf{g}}_tp)-U(x).\end{align*} $$
Since
![]() $\mathcal J_{-c}=-\mathcal J_c$
is Livšic-cohomologous to a strictly negative function, the above equation implies that the flow
$\mathcal J_{-c}=-\mathcal J_c$
is Livšic-cohomologous to a strictly negative function, the above equation implies that the flow
![]() $\hat {\mathsf {g}}$
is contracting on
$\hat {\mathsf {g}}$
is contracting on
![]() ${\mathsf {F}},$
that is, there exist positive C and
${\mathsf {F}},$
that is, there exist positive C and
![]() $\mu $
such that for all
$\mu $
such that for all
![]() $v\in {\mathsf {F}}$
and
$v\in {\mathsf {F}}$
and
![]() $t\in \mathbb {R}$
, one has
$t\in \mathbb {R}$
, one has
A standard procedure (see for example [Reference Katok and Hasselblatt41] or [Reference Bridgeman, Canary, Labourie and Sambarino17, Lemma 4.3]) provides a Euclidean metric
![]() $\|\,\|$
on
$\|\,\|$
on
![]() ${\mathsf {F}}$
such that the constant C equals
${\mathsf {F}}$
such that the constant C equals
![]() $1.$
We denote also by
$1.$
We denote also by
![]() $\|\,\|$
the lift of this metric to
$\|\,\|$
the lift of this metric to
![]() it is a
it is a
![]() -invariant family.
-invariant family.
Given then
![]() , we let
, we let
![]() $v_{(x,y,t)}\in (\mathbb {R}-\{0\})/\pm $
be such that
$v_{(x,y,t)}\in (\mathbb {R}-\{0\})/\pm $
be such that
![]() $\|v_{(x,y,t)}\|=1.$
As in [Reference Bridgeman, Canary, Labourie and Sambarino17, Proposition 4.2], the map
$\|v_{(x,y,t)}\|=1.$
As in [Reference Bridgeman, Canary, Labourie and Sambarino17, Proposition 4.2], the map

is
![]() -equivariant and an orbit equivalence between the
-equivariant and an orbit equivalence between the
![]() $\mathbb {R}$
-actions.
$\mathbb {R}$
-actions.
Definition 3.2.3. The flow
![]() $\phi ^c$
will be called the refraction flow of
$\phi ^c$
will be called the refraction flow of
![]() $c.$
$c.$
3.3 Patterson–Sullivan measures
Let us consider now Hölder cocycles with
![]() $V=\mathbb {R}$
and only depending on one variable, that is,
$V=\mathbb {R}$
and only depending on one variable, that is,
![]() Assume moreover that c has non-negative periods and finite entropy. A cocycle
Assume moreover that c has non-negative periods and finite entropy. A cocycle
![]() is dual to c if for every hyperbolic
is dual to c if for every hyperbolic
![]() , one has
, one has
Definition 3.3.1
-
• A Patterson–Sullivan measure for c of exponent
 $\delta \in \mathbb {R}_+$
is a probability measure
$\delta \in \mathbb {R}_+$
is a probability measure
 $\mu $
on
$\mu $
on
 such that for every
such that for every
 , one has (14)
, one has (14) $$ \begin{align}\frac{d \gamma_*\mu}{\,d\mu}(\cdot)=e^{-\delta c(\gamma^{-1},\cdot)}.\end{align} $$
$$ \begin{align}\frac{d \gamma_*\mu}{\,d\mu}(\cdot)=e^{-\delta c(\gamma^{-1},\cdot)}.\end{align} $$
-
• A Gromov product for the ordered pair
 $(\bar c, c)$
is a function
$(\bar c, c)$
is a function
 such that for all
such that for all
 and
and
 , one has
, one has  $$ \begin{align*}[\gamma x,\gamma y]-[x,y]=-(\bar c(\gamma,x)+c(\gamma,y)).\end{align*} $$
$$ \begin{align*}[\gamma x,\gamma y]-[x,y]=-(\bar c(\gamma,x)+c(\gamma,y)).\end{align*} $$
Consider a pair of dual cocycles
![]() $(\bar c,c)$
and assume a Patterson–Sullivan measure of exponent
$(\bar c,c)$
and assume a Patterson–Sullivan measure of exponent
![]() $\delta $
exists for each c and
$\delta $
exists for each c and
![]() $\bar c,$
denoted by
$\bar c,$
denoted by
![]() $\mu $
and
$\mu $
and
![]() $\bar \mu $
, respectively. Assume moreover that a Gromov product for the pair
$\bar \mu $
, respectively. Assume moreover that a Gromov product for the pair
![]() $(\bar c, c)$
exists. The measure
$(\bar c, c)$
exists. The measure
on
is hence
-invariant (the action being via
![]() $c,$
as in equation (12) and
$c,$
as in equation (12) and
![]() $\mathbb {R}$
-invariant. Passing to the quotient, one obtains a measure
$\mathbb {R}$
-invariant. Passing to the quotient, one obtains a measure
![]() $\mathscr m$
on
$\mathscr m$
on
![]() ${\unicode{x3c7} ^{c}}$
invariant under the flow
${\unicode{x3c7} ^{c}}$
invariant under the flow
![]() $\phi ^c.$
Observe that we can write
$\phi ^c.$
Observe that we can write
![]() $\widetilde {\mathscr m}$
as
$\widetilde {\mathscr m}$
as

The measure
![]() $e^{-\delta t}\,d\mu \,dt$
is
$e^{-\delta t}\,d\mu \,dt$
is
-invariant on
(indeed, if
is continuous, then
 $$ \begin{align*}\int f(\gamma(y,t))e^{-\delta t} \,d\mu \,dt,&=\int f(\gamma y,t-c(\gamma,y))e^{-\delta t} \,d\mu \,dt & \\& =\int f(\gamma y,t)e^{-\delta (t-c(\gamma,y))} \,d\mu \,dt \,\quad\qquad\textrm{(by translation invariance)}&\\& =\int f( y,t)e^{-\delta (t-c(\gamma,\gamma^{-1}y))}e^{-\delta c(\gamma^{-1},y)} \,d\mu \,dt \quad\textrm{(by definition of }\mu)&\\& =\int f(y,t)e^{-\delta t}\,d\mu \,dt)& \end{align*} $$
$$ \begin{align*}\int f(\gamma(y,t))e^{-\delta t} \,d\mu \,dt,&=\int f(\gamma y,t-c(\gamma,y))e^{-\delta t} \,d\mu \,dt & \\& =\int f(\gamma y,t)e^{-\delta (t-c(\gamma,y))} \,d\mu \,dt \,\quad\qquad\textrm{(by translation invariance)}&\\& =\int f( y,t)e^{-\delta (t-c(\gamma,\gamma^{-1}y))}e^{-\delta c(\gamma^{-1},y)} \,d\mu \,dt \quad\textrm{(by definition of }\mu)&\\& =\int f(y,t)e^{-\delta t}\,d\mu \,dt)& \end{align*} $$
and the family
is
-equivariant.
This decomposition induces then a local decomposition of
![]() $\mathscr m$
as a product of measures on the laminations induced on the quotient by
$\mathscr m$
as a product of measures on the laminations induced on the quotient by
![]() and
and
![]() The local product structure induced by
The local product structure induced by
![]() permits to transport the measures
permits to transport the measures
![]() $m_{(y,t)},$
parallel to the central stable leaf
$m_{(y,t)},$
parallel to the central stable leaf
![]() $W^{\mathrm {cu}}[(x,y,t)],$
to the stable leaf of
$W^{\mathrm {cu}}[(x,y,t)],$
to the stable leaf of
![]() $[(x,y,t)]$
for
$[(x,y,t)]$
for
![]() $\phi ^c$
to obtain a family of measures at each strong stable leaf
$\phi ^c$
to obtain a family of measures at each strong stable leaf
![]() $\nu ^{{\mathrm {s}}}_p$
such that
$\nu ^{{\mathrm {s}}}_p$
such that
 $$ \begin{align}\frac{d(\phi^c_{-t})_*\nu^{{\mathrm{s}}}_p}{\,d\nu^{{\mathrm{s}}}_{\phi^c_tp}}=e^{-\delta t}.\end{align} $$
$$ \begin{align}\frac{d(\phi^c_{-t})_*\nu^{{\mathrm{s}}}_p}{\,d\nu^{{\mathrm{s}}}_{\phi^c_tp}}=e^{-\delta t}.\end{align} $$
Margulis’s description of the measure maximizing entropy (§2.3.4) then gives that
![]() $\delta =\mathscr h_c$
and that
$\delta =\mathscr h_c$
and that
![]() $\mathscr m$
maximizes entropy for
$\mathscr m$
maximizes entropy for
![]() $\phi ^c.$
Thus, subject to the existence of the Patterson–Sullivan measures and the Gromov product, we summarize the above discussion in the following proposition.
$\phi ^c.$
Thus, subject to the existence of the Patterson–Sullivan measures and the Gromov product, we summarize the above discussion in the following proposition.
Proposition 3.3.2. The measure
![]() $\mathscr m$
on
$\mathscr m$
on
![]() ${\unicode{x3c7} ^{c}}$
maximizes entropy for the flow
${\unicode{x3c7} ^{c}}$
maximizes entropy for the flow
![]() $\phi ^c.$
The exponent
$\phi ^c.$
The exponent
![]() $\delta $
necessarily equals the topological entropy of
$\delta $
necessarily equals the topological entropy of
![]() $\phi ^c, \mathscr h_c,$
if
$\phi ^c, \mathscr h_c,$
if
![]() $\nu $
is another Patterson–Sullivan measure for c then
$\nu $
is another Patterson–Sullivan measure for c then
![]() $\nu =\mu .$
$\nu =\mu .$
Let us consider again the measure
![]() $\widetilde {\mathscr m}$
on
$\widetilde {\mathscr m}$
on
![]() from equation (15) but let us instead study the
from equation (15) but let us instead study the
![]() -action on the
-action on the
![]() $\mathbb {R}$
-coordinate by the Gromov–Mineyev cocycle, so that
$\mathbb {R}$
-coordinate by the Gromov–Mineyev cocycle, so that
![]() and the induced flow is
and the induced flow is
![]() ${\mathsf {g}}.$
The quotient measure,
${\mathsf {g}}.$
The quotient measure,
![]() $\mathscr a,$
is
$\mathscr a,$
is
![]() ${\mathsf {g}}$
-invariant and the orbit equivalence
${\mathsf {g}}$
-invariant and the orbit equivalence
![]() $\unicode{x3be} $
from equation (13) preserves, by the way it is defined, zero flow-invariant sets between
$\unicode{x3be} $
from equation (13) preserves, by the way it is defined, zero flow-invariant sets between
![]() $\mathscr a$
and
$\mathscr a$
and
![]() $\mathscr m.$
Since
$\mathscr m.$
Since
![]() $\unicode{x3be} $
is a conjugation between
$\unicode{x3be} $
is a conjugation between
![]() ${\mathsf {g}}^{\mathcal J_c}$
and
${\mathsf {g}}^{\mathcal J_c}$
and
![]() $\phi ^c,$
and
$\phi ^c,$
and
![]() $\mathscr m$
maximizes entropy for
$\mathscr m$
maximizes entropy for
![]() $\phi ^c,$
the measure
$\phi ^c,$
the measure
![]() $\unicode{x3be} _*\mathscr m$
is
$\unicode{x3be} _*\mathscr m$
is
![]() ${\mathsf {g}}^{\mathcal J_c}$
-invariant, maximizes entropy for
${\mathsf {g}}^{\mathcal J_c}$
-invariant, maximizes entropy for
![]() ${\mathsf {g}}^{\mathcal J_c}$
, and has the same zero sets as
${\mathsf {g}}^{\mathcal J_c}$
, and has the same zero sets as
![]() $\mathscr a.$
$\mathscr a.$
One concludes that the Abramov transform in equation (3)
![]() ${\mathscr a}^\#$
(with respect to
${\mathscr a}^\#$
(with respect to
![]() $\mathcal J_c$
) is a measure of maximal entropy of the flow
$\mathcal J_c$
) is a measure of maximal entropy of the flow
![]() ${\mathsf {g}}^{\mathcal J_c}.$
Lemma 2.1.1 implies then that
${\mathsf {g}}^{\mathcal J_c}.$
Lemma 2.1.1 implies then that
![]() $\mathscr a/|\mathscr a|$
is the equilibrium state of
$\mathscr a/|\mathscr a|$
is the equilibrium state of
![]() $-\mathscr h_c\mathcal J_c.$
Let us summarize in the following remark.
$-\mathscr h_c\mathcal J_c.$
Let us summarize in the following remark.
Remark 3.3.3. The probability measure
![]() $\mathscr a/|\mathscr a|$
on
$\mathscr a/|\mathscr a|$
on
![]() induced by
induced by
![]() $\widetilde {\mathscr m}$
is the equilibrium state of
$\widetilde {\mathscr m}$
is the equilibrium state of
![]() $-\mathscr h_c\mathcal J_c.$
$-\mathscr h_c\mathcal J_c.$
Since the zero sets of an equilibrium state are uniquely determined by the Livšic-cohomology class of the associated potential up to an additive constant (Theorem 2.3.3), one concludes the following corollary.
Corollary 3.3.4. Let
![]() $\bar \kappa ,\kappa $
be a pair of dual cocycles with non-negative periods and finite entropy. Assume Patterson—Sullivan measures,
$\bar \kappa ,\kappa $
be a pair of dual cocycles with non-negative periods and finite entropy. Assume Patterson—Sullivan measures,
![]() $\nu $
and
$\nu $
and
![]() $\bar \nu ,$
exist for
$\bar \nu ,$
exist for
![]() $\kappa $
and
$\kappa $
and
![]() $\bar \kappa $
, respectively, together with a Gromov product for the pair. If
$\bar \kappa $
, respectively, together with a Gromov product for the pair. If
![]() $\nu $
has the same zero sets as
$\nu $
has the same zero sets as
![]() $\mu $
, then the (scaled) Ledrappier potentials
$\mu $
, then the (scaled) Ledrappier potentials
![]() $\mathscr h_c\mathcal J_c$
and
$\mathscr h_c\mathcal J_c$
and
![]() $\mathscr h_\kappa \mathcal J_\kappa $
are Livšic-cohomologous and
$\mathscr h_\kappa \mathcal J_\kappa $
are Livšic-cohomologous and
![]() $\nu =\mu .$
$\nu =\mu .$
Proof. A final argument is required, indeed from §2.3.3, there exists a constant K such that
![]() $\mathscr h_c\mathcal J_c$
and
$\mathscr h_c\mathcal J_c$
and
![]() $\mathscr h_\kappa \mathcal J_\kappa +K$
are Livšic-cohomologous. However, since
$\mathscr h_\kappa \mathcal J_\kappa +K$
are Livšic-cohomologous. However, since
![]() $\mathscr h_c$
is the topological entropy of
$\mathscr h_c$
is the topological entropy of
![]() ${\mathsf {g}}^{\mathcal J_c},$
Lemma 2.1.1 gives
${\mathsf {g}}^{\mathcal J_c},$
Lemma 2.1.1 gives
where the second equality holds by Remark 2.1.2, and the third equality by the definition of P (equation (2)).
The above corollary was reported by Ledrappier [Reference Ledrappier44] when
![]() is the fundamental group of a negatively curved closed manifold. The proof uses also a disintegration argument. One may also check [Reference Kaimanovich39] and Babillot’s survey [Reference Babillot4] specifically for the Buseman cocycle (
is the fundamental group of a negatively curved closed manifold. The proof uses also a disintegration argument. One may also check [Reference Kaimanovich39] and Babillot’s survey [Reference Babillot4] specifically for the Buseman cocycle (
![]() as in Ledrappier’s aforementioned situation), and [Reference Carvajales23, Appendix] for the refraction cocycle
as in Ledrappier’s aforementioned situation), and [Reference Carvajales23, Appendix] for the refraction cocycle
![]() $\unicode{x3b2} _{\varphi }$
(see §5.3 for the definition) of a
$\unicode{x3b2} _{\varphi }$
(see §5.3 for the definition) of a
![]() ${{{\Delta }}}$
-Anosov representation of an arbitrary word-hyperbolic group.
${{{\Delta }}}$
-Anosov representation of an arbitrary word-hyperbolic group.
3.4 Vector-valued cocycles I: the critical hypersurface
Let now
be a Hölder cocycle and consider the compact convex set
![]() $\mathcal M^{\mathsf {g}}(\mathcal J_c)\subset V.$
Since this set depends on the base flow
$\mathcal M^{\mathsf {g}}(\mathcal J_c)\subset V.$
Since this set depends on the base flow
![]() ${\mathsf {g}}$
, it is natural to consider the limit cone of c:
${\mathsf {g}}$
, it is natural to consider the limit cone of c:

Remark 3.4.1. Up to Livšic-cohomology, we can assume that
![]() $\mathcal J_c$
has values in the vector space
$\mathcal J_c$
has values in the vector space
![]() $V'=\langle\mathcal M^{\mathsf {g}}(\mathcal J_c)\rangle .$
We can moreover choose a reparameterization
$V'=\langle\mathcal M^{\mathsf {g}}(\mathcal J_c)\rangle .$
We can moreover choose a reparameterization
![]() ${\mathsf {g}}^f$
of
${\mathsf {g}}^f$
of
![]() ${\mathsf {g}}$
so that if
${\mathsf {g}}$
so that if
![]() is the Ledrappier potential for c over
is the Ledrappier potential for c over
![]() ${\mathsf {g}}^f$
, then the flow
${\mathsf {g}}^f$
, then the flow
![]() ${\mathsf {g}}^f$
together with the potential
${\mathsf {g}}^f$
together with the potential
![]() $\mathcal J_c^{\mathsf {g^f}}\!$
verify Assumption A from §2.6.
$\mathcal J_c^{\mathsf {g^f}}\!$
verify Assumption A from §2.6.
Proof. By Remark 2.2.7, the space of Livšic-cohomology classes over
![]() ${\mathsf {g}}$
is infinite dimensional, so the remark follows.
${\mathsf {g}}$
is infinite dimensional, so the remark follows.
We will work from now on with flow
![]() ${\mathsf {g}}^f$
given by the remark and the Ledrappier potential
${\mathsf {g}}^f$
given by the remark and the Ledrappier potential
![]() $\mathcal J_c^{\mathsf {g^f}}.$
We will rename these by
$\mathcal J_c^{\mathsf {g^f}}.$
We will rename these by
![]() ${\mathsf {g}}$
and
${\mathsf {g}}$
and
![]() $\mathcal J_c$
though as to not overcharge the paper with notation and keep in mind that when we restrict the image of
$\mathcal J_c$
though as to not overcharge the paper with notation and keep in mind that when we restrict the image of
![]() $\mathcal J_c$
to
$\mathcal J_c$
to
![]() $V',$
Assumption A is verified.
$V',$
Assumption A is verified.
Let
![]() $(\mathscr L_c)^*=\{\psi \in V^*:\psi |\mathscr L_c\geq 0\}$
be the dual cone of
$(\mathscr L_c)^*=\{\psi \in V^*:\psi |\mathscr L_c\geq 0\}$
be the dual cone of
![]() $c.$
For
$c.$
For
![]() $\psi \in V^*$
, denote
$\psi \in V^*$
, denote
![]() and
and
![]() $\mathscr h_\psi =\mathscr h_{c_\psi }.$
$\mathscr h_\psi =\mathscr h_{c_\psi }.$
Assumption C. There exists
![]() $\psi \in (\mathscr L_c)^*$
such that
$\psi \in (\mathscr L_c)^*$
such that
![]() $c_\psi $
has finite entropy.
$c_\psi $
has finite entropy.
Lemma 3.4.2. In this case,
![]() $0\notin \mathcal M^{\mathsf {g}}(\mathcal J_c), (\mathscr L_c)^*$
has non-empty interior, and
$0\notin \mathcal M^{\mathsf {g}}(\mathcal J_c), (\mathscr L_c)^*$
has non-empty interior, and
![]() $\operatorname {\mathrm {int}}(\mathscr L_c)^*=\{\varphi \in (\mathscr L_c)^*:\mathscr h_\varphi <\infty \}.$
$\operatorname {\mathrm {int}}(\mathscr L_c)^*=\{\varphi \in (\mathscr L_c)^*:\mathscr h_\varphi <\infty \}.$
Proof. The lemma follows essentially from §3.1 and Lemma 2.2.7, indeed since
![]() $\mathscr h_{\psi }=\mathscr h_{\psi (\mathcal J_c)}<\infty $
, there exists
$\mathscr h_{\psi }=\mathscr h_{\psi (\mathcal J_c)}<\infty $
, there exists
![]() $\kappa>0$
such that for all hyperbolic
$\kappa>0$
such that for all hyperbolic
![]() , it holds
, it holds
![]() $\psi (\ell _c(\gamma )/p(\gamma ))>\kappa ;$
by density of periodic orbits on
$\psi (\ell _c(\gamma )/p(\gamma ))>\kappa ;$
by density of periodic orbits on
![]() $\mathcal M^{\mathsf {g}}$
, one has
$\mathcal M^{\mathsf {g}}$
, one has
![]() $\inf \{\psi (\mathcal M^{\mathsf {g}}(\mathcal J_c))\}>\kappa >0.$
The remaining statements follow similarly.
$\inf \{\psi (\mathcal M^{\mathsf {g}}(\mathcal J_c))\}>\kappa >0.$
The remaining statements follow similarly.
Since
![]() $0\notin \mathcal M^{\phi ^{c_\psi }}(\mathcal J_c)$
, we can apply Corollary 2.6. Denote by
$0\notin \mathcal M^{\phi ^{c_\psi }}(\mathcal J_c)$
, we can apply Corollary 2.6. Denote by

respectively the critical hypersurface and the convergence domain of
![]() $c.$
$c.$
Since we have not required the cone
![]() $\mathscr L_c$
to have non-empty interior, consider its annihilation space
$\mathscr L_c$
to have non-empty interior, consider its annihilation space
If
![]() $\varphi \in \operatorname {\mathrm {int}}(\mathscr L_c)^*$
and
$\varphi \in \operatorname {\mathrm {int}}(\mathscr L_c)^*$
and
![]() $\psi \in \mathrm {Ann}(\mathscr L_c)$
, then the potentials
$\psi \in \mathrm {Ann}(\mathscr L_c)$
, then the potentials
![]() $\varphi (\mathcal J_c)$
and
$\varphi (\mathcal J_c)$
and
![]() $(\varphi +\psi )(\mathcal J_c)$
are Livšic-cohomologous. Let
$(\varphi +\psi )(\mathcal J_c)$
are Livšic-cohomologous. Let
![]() $\pi ^c:V^*\to V^*/\mathrm {Ann}(\mathscr L_c)$
be the quotient projection.
$\pi ^c:V^*\to V^*/\mathrm {Ann}(\mathscr L_c)$
be the quotient projection.
We also import the concept of dynamical intersection of §2.7 to this setting using the Ledrappier potential of
![]() $c.$
For
$c.$
For
![]() $\varphi \in \mathcal Q_c$
, define the dynamical intersection map associated to c by
$\varphi \in \mathcal Q_c$
, define the dynamical intersection map associated to c by
![]() $\mathbf {I}_\varphi =\mathbf {I}^c_\varphi :V^*\to \mathbb {R}$
be defined by
$\mathbf {I}_\varphi =\mathbf {I}^c_\varphi :V^*\to \mathbb {R}$
be defined by
By definition,
![]() $\mathbf {I}(\varphi (\mathcal J_c),\psi (\mathcal J_c))$
only depends on the Livšic-cohomology classes of
$\mathbf {I}(\varphi (\mathcal J_c),\psi (\mathcal J_c))$
only depends on the Livšic-cohomology classes of
![]() $\varphi (\mathcal J_c)$
and
$\varphi (\mathcal J_c)$
and
![]() $\psi (\mathcal J_c),$
so we may freely consider
$\psi (\mathcal J_c),$
so we may freely consider
![]() $\mathbf {I}$
as defined on
$\mathbf {I}$
as defined on
![]() $\mathcal Q_c\times V^*$
or on
$\mathcal Q_c\times V^*$
or on
![]() $\pi ^c(\mathcal Q_c)\times V^*/\mathrm {Ann}(\mathscr L_c).$
One has the following corollary.
$\pi ^c(\mathcal Q_c)\times V^*/\mathrm {Ann}(\mathscr L_c).$
One has the following corollary.
Corollary 3.4.3. Under Assumption C, one has that
![]() $\pi ^c(\mathcal D_c)$
is a strictly convex set whose boundary is
$\pi ^c(\mathcal D_c)$
is a strictly convex set whose boundary is
![]() $\pi ^c(\mathcal Q_c).$
The latter is an analytic co-dimension-one sub-manifold. The map
$\pi ^c(\mathcal Q_c).$
The latter is an analytic co-dimension-one sub-manifold. The map
![]() ${\mathsf {u}}:\pi ^c(\mathcal Q_c)\to \mathbb {P}(\operatorname {\mathrm {span}}\{\mathscr L_c\})$
defined by
${\mathsf {u}}:\pi ^c(\mathcal Q_c)\to \mathbb {P}(\operatorname {\mathrm {span}}\{\mathscr L_c\})$
defined by
is an analytic diffeomorphism between
![]() $\pi ^c(\mathcal Q_c)$
and directions in the relative interior of
$\pi ^c(\mathcal Q_c)$
and directions in the relative interior of
![]() $\mathscr L_c.$
$\mathscr L_c.$
3.5 Vector-valued cocycles II: skew-product structure
We remain in the situation of §3.4, that is, we keep Assumption C. It follows at once from Theorem 3.2 that the
![]() -action
-action
![]()
is properly discontinuous. We aim to give a description of the V-action on the quotient space
![]() .
.
By Lemma 3.4.2 and Theorem 3.2.2, we can, for every
![]() $\varphi \in \operatorname {\mathrm {int}}(\mathscr L_c)^*,$
consider the refraction flow
$\varphi \in \operatorname {\mathrm {int}}(\mathscr L_c)^*,$
consider the refraction flow
![]() $\phi ^{c_\varphi }=(\phi ^{c_\varphi }_t:{\unicode{x3c7} ^{c_\varphi }}\to {\unicode{x3c7} ^{c_\varphi }})_{t\in \mathbb {R}}.$
Such a
$\phi ^{c_\varphi }=(\phi ^{c_\varphi }_t:{\unicode{x3c7} ^{c_\varphi }}\to {\unicode{x3c7} ^{c_\varphi }})_{t\in \mathbb {R}}.$
Such a
![]() $\varphi $
is fixed from now on.
$\varphi $
is fixed from now on.
Remark 3.5.1. Let us still denote by
![]() $\mathcal J_c$
the Ledrappier potential for c over the flow
$\mathcal J_c$
the Ledrappier potential for c over the flow
![]() $\phi ^{c_\varphi },$
that is, for every hyperbolic
$\phi ^{c_\varphi },$
that is, for every hyperbolic
![]() , one has
, one has
 $$ \begin{align*}\int_{[\gamma]}\mathcal J_c=\ell_c(\gamma)\in V.\end{align*} $$
$$ \begin{align*}\int_{[\gamma]}\mathcal J_c=\ell_c(\gamma)\in V.\end{align*} $$
Let
![]() $\mathscr p$
be the probability measure of maximal entropy of
$\mathscr p$
be the probability measure of maximal entropy of
![]() $\phi ^{c_\varphi }.$
The growth direction of
$\phi ^{c_\varphi }.$
The growth direction of
![]() $\varphi $
is the line of V
$\varphi $
is the line of V
 $$ \begin{align}{\mathsf{u}}_\varphi={\mathsf{T}}_\varphi\mathcal Q_c= \mathbb{R}\cdot\int_{{\unicode{x3c7}^{c_\varphi}}}\mathcal J_c d\mathscr p\end{align} $$
$$ \begin{align}{\mathsf{u}}_\varphi={\mathsf{T}}_\varphi\mathcal Q_c= \mathbb{R}\cdot\int_{{\unicode{x3c7}^{c_\varphi}}}\mathcal J_c d\mathscr p\end{align} $$
(the last equality follows from equation (9) and Corollary 2.6.4). Consider also the projection
![]() $\pi ^\varphi :V\to \ker \varphi $
parallel to
$\pi ^\varphi :V\to \ker \varphi $
parallel to
![]() ${\mathsf {u}}_\varphi $
and denote by
${\mathsf {u}}_\varphi $
and denote by
![]() $\mathcal J_c^\varphi :{\unicode{x3c7} ^{c_\varphi }}\to \ker \varphi $
the composition
$\mathcal J_c^\varphi :{\unicode{x3c7} ^{c_\varphi }}\to \ker \varphi $
the composition
![]() $\mathcal J_c^\varphi =\pi ^\varphi \circ \mathcal J_c.$
Observe that
$\mathcal J_c^\varphi =\pi ^\varphi \circ \mathcal J_c.$
Observe that
 $$ \begin{align} \int_{{\unicode{x3c7}^{c_\varphi}}} \mathcal J_c^\varphi d\mathscr p=0.\end{align} $$
$$ \begin{align} \int_{{\unicode{x3c7}^{c_\varphi}}} \mathcal J_c^\varphi d\mathscr p=0.\end{align} $$
Fix
![]() $u_\varphi \in {\mathsf {u}}_\varphi $
with
$u_\varphi \in {\mathsf {u}}_\varphi $
with
![]() $\varphi (u_\varphi )=1$
and define the directional flow
$\varphi (u_\varphi )=1$
and define the directional flow
![]() by induction on the quotient of
by induction on the quotient of
Proposition 3.5.2. (Sambarino [Reference Sambarino66])
There exists a (bi)-Hölder-continuous homeomorphism
commuting with the
![]() $\ker \varphi $
action, that conjugates the flow
$\ker \varphi $
action, that conjugates the flow
![]() $\unicode{x3c9} ^\varphi $
with
$\unicode{x3c9} ^\varphi $
with
![]() $\Phi ^\varphi =(\Phi _t^\varphi :{\unicode{x3c7} ^{c_\varphi }}\times \ker \varphi \to {\unicode{x3c7} ^{c_\varphi }}\times \ker \varphi )_{t\in \mathbb {R}}$
$\Phi ^\varphi =(\Phi _t^\varphi :{\unicode{x3c7} ^{c_\varphi }}\times \ker \varphi \to {\unicode{x3c7} ^{c_\varphi }}\times \ker \varphi )_{t\in \mathbb {R}}$
 $$ \begin{align*}{\displaystyle\Phi_t^\varphi(p,v):=\bigg(\phi^{c_\varphi}_t(p),v-\int_0^t\mathcal J_c^\varphi(\phi^{c_\varphi}_s p)\,ds\bigg).}\end{align*} $$
$$ \begin{align*}{\displaystyle\Phi_t^\varphi(p,v):=\bigg(\phi^{c_\varphi}_t(p),v-\int_0^t\mathcal J_c^\varphi(\phi^{c_\varphi}_s p)\,ds\bigg).}\end{align*} $$
Proof. This is the first item of Sambarino [Reference Sambarino66, Proposition 3.5] when
![]() is the fundamental group of a closed negatively curved manifold. The proof adapts mutatis mutandis once §3.2 is established.
is the fundamental group of a closed negatively curved manifold. The proof adapts mutatis mutandis once §3.2 is established.
Let us moreover place ourselves in the existence assumptions of §3.3 for the cocycle
![]() $c_\varphi ,$
that is, assume there exists:
$c_\varphi ,$
that is, assume there exists:
-
• a dual cocycle
 $\bar c_\varphi $
together with a Gromov product
$\bar c_\varphi $
together with a Gromov product
 $[\cdot ,\cdot ]$
for the pair
$[\cdot ,\cdot ]$
for the pair
 $(\bar c_\varphi ,c_\varphi );$
$(\bar c_\varphi ,c_\varphi );$
-
• a Patterson–Sullivan measure for each
 $c_\varphi $
and
$c_\varphi $
and
 $\bar c_\varphi ,$
denoted by
$\bar c_\varphi ,$
denoted by
 $\mu $
and
$\mu $
and
 $\bar \mu $
, respectively. Recall from Proposition 3.3.2 that, necessarily, the exponent of both
$\bar \mu $
, respectively. Recall from Proposition 3.3.2 that, necessarily, the exponent of both
 $\mu $
and
$\mu $
and
 $\bar \mu $
is
$\bar \mu $
is
 $\mathscr h_{c_\varphi },$
the topological entropy of
$\mathscr h_{c_\varphi },$
the topological entropy of
 $\phi ^{c_\varphi }.$
$\phi ^{c_\varphi }.$
By Proposition 3.3.2, the measure
![]() $\mathscr m$
maximizes entropy for
$\mathscr m$
maximizes entropy for
![]() $\phi ^{c_\varphi }.$
One has then
$\phi ^{c_\varphi }.$
One has then
![]() $\mathscr p=\mathscr m/|\mathscr m|.$
Consider the
$\mathscr p=\mathscr m/|\mathscr m|.$
Consider the
![]() $\varphi $
-Bowen–Margulis measure
$\varphi $
-Bowen–Margulis measure
![]() $\Omega ^\varphi $
on
$\Omega ^\varphi $
on
![]() defined as induction on the quotient by
defined as induction on the quotient by
for a Lebesgue measure on
![]() $V.$
One has the following result.
$V.$
One has the following result.
Proposition 3.5.3. (Sambarino [Reference Sambarino66])
The (bi)-Hölder-continuous homeomorphism from Proposition 3.5.2 is a measurable isomorphism between
![]() $\Omega ^\varphi $
and
$\Omega ^\varphi $
and
![]() $\mathscr m\otimes \operatorname {\mathrm {Leb}}_{\ker \varphi }\!.$
$\mathscr m\otimes \operatorname {\mathrm {Leb}}_{\ker \varphi }\!.$
Proof. This follows again as in [Reference Sambarino66, Proposition 3.5] once Proposition 3.3.2 is established.
3.6 Vector-valued cocycles III: dynamical consequences
We remain in the situation of §3.4. Let us say that c is non-arithmetic if the periods of c span a dense subgroup in
![]() $V.$
$V.$
One concludes at once the following consequences.
Corollary 3.6.1. (Ergodicity dichotomy)
Assume c is non-arithmetic, then
![]() $\unicode{x3c9} ^\varphi $
is mixing as in Theorem 2.5.2, consequently if
$\unicode{x3c9} ^\varphi $
is mixing as in Theorem 2.5.2, consequently if
![]() $\dim V\geq 4$
, then
$\dim V\geq 4$
, then
![]() $\mathcal K(\unicode{x3c9} ^\varphi )$
has zero
$\mathcal K(\unicode{x3c9} ^\varphi )$
has zero
![]() $\Omega ^\varphi $
-measure. If
$\Omega ^\varphi $
-measure. If
![]() $\dim V\leq 2$
, then the directional flow
$\dim V\leq 2$
, then the directional flow
![]() $\unicode{x3c9} ^\varphi $
is
$\unicode{x3c9} ^\varphi $
is
![]() $\Omega ^\varphi $
-ergodic.
$\Omega ^\varphi $
-ergodic.
Proof. By Proposition 3.5.2, the flow
![]() $\unicode{x3c9} ^\varphi $
is Hölder-conjugated to the skew-product of
$\unicode{x3c9} ^\varphi $
is Hölder-conjugated to the skew-product of
![]() $\phi ^{c_\varphi }$
with the Ledrappier potential
$\phi ^{c_\varphi }$
with the Ledrappier potential
![]() $\mathcal J_c^\varphi ,$
the fiber being
$\mathcal J_c^\varphi ,$
the fiber being
![]() $\ker \varphi $
and thus
$\ker \varphi $
and thus
![]() $\dim V-1$
-dimensional. Proposition 3.5.3 describes the desired measures in terms of the skew-product structure; non-arithmeticity of c and equation (18) allow us to apply Corollary 2.5.5.
$\dim V-1$
-dimensional. Proposition 3.5.3 describes the desired measures in terms of the skew-product structure; non-arithmeticity of c and equation (18) allow us to apply Corollary 2.5.5.
4 Algebraic semi-simple groups over a local field
This section is a collection of necessary language and basic results needed for the following section. Most of the material covered here can be found in, for example, Borel’s book [Reference Borel12] and/or in the book by Benoist and Quint [Reference Benoist and Quint9].
Let
![]() $\mathbb {K}$
be a local field. If
$\mathbb {K}$
be a local field. If
![]() $\mathbb {K}$
is non-Archimedean, let us denote by q the cardinality of its residue field,
$\mathbb {K}$
is non-Archimedean, let us denote by q the cardinality of its residue field,
![]() $u\in \mathbb {K}$
a uniformizing element, and choose the norm
$u\in \mathbb {K}$
a uniformizing element, and choose the norm
![]() $|\,|$
on
$|\,|$
on
![]() $\mathbb {K}$
so that
$\mathbb {K}$
so that
![]() $|u|=q^{-1}.$
In this case,
$|u|=q^{-1}.$
In this case,
![]() $\log $
denotes the logarithm on base
$\log $
denotes the logarithm on base
![]() $q,$
so that
$q,$
so that
![]() $\log q=1.$
If
$\log q=1.$
If
![]() $\mathbb {K}=\mathbb {R}$
or
$\mathbb {K}=\mathbb {R}$
or
![]() $\mathbb {C}$
, then
$\mathbb {C}$
, then
![]() $|\,|$
is the standard modulus,
$|\,|$
is the standard modulus,
![]() $q:=e$
, and
$q:=e$
, and
![]() $\log $
is the usual logarithm.
$\log $
is the usual logarithm.
Let
![]() ${\mathsf {G}}$
be the
${\mathsf {G}}$
be the
![]() $\mathbb {K}$
-points of a connected semi-simple
$\mathbb {K}$
-points of a connected semi-simple
![]() $\mathbb {K}$
-group,
$\mathbb {K}$
-group,
![]() ${\mathsf {A}}$
the
${\mathsf {A}}$
the
![]() $\mathbb {K}$
-points of a maximal
$\mathbb {K}$
-points of a maximal
![]() $\mathbb {K}$
-split torus, and
$\mathbb {K}$
-split torus, and
![]() $\mathbf {X}({\mathsf {A}})$
the group of its
$\mathbf {X}({\mathsf {A}})$
the group of its
![]() $\mathbb {K}^*$
-characters. Consider the real vector space
$\mathbb {K}^*$
-characters. Consider the real vector space
![]() ${\mathsf {E}}^*=\mathbf {X}({\mathsf {A}})\otimes _{\mathbb {Z}}\mathbb {R}$
and
${\mathsf {E}}^*=\mathbf {X}({\mathsf {A}})\otimes _{\mathbb {Z}}\mathbb {R}$
and
![]() ${\mathsf {E}}$
its dual. For every
${\mathsf {E}}$
its dual. For every
![]() $\chi \in \mathbf X({\mathsf {A}}),$
we denote by
$\chi \in \mathbf X({\mathsf {A}}),$
we denote by
![]() $\chi ^\omega $
the corresponding linear form on
$\chi ^\omega $
the corresponding linear form on
![]() ${\mathsf {E}}.$
${\mathsf {E}}.$
Let
![]() ${{{\Phi }}}$
be the set of restricted roots of
${{{\Phi }}}$
be the set of restricted roots of
![]() ${\mathsf {A}}$
in
${\mathsf {A}}$
in
![]() $\mathfrak g,$
the set
$\mathfrak g,$
the set
![]() ${{{\Phi }}}^\omega $
is a root system of
${{{\Phi }}}^\omega $
is a root system of
![]() ${\mathsf {E}}^*.$
Let
${\mathsf {E}}^*.$
Let
![]() $({{{\Phi }}}^\omega )^+$
be a system of positive roots,
$({{{\Phi }}}^\omega )^+$
be a system of positive roots,
![]() ${\mathsf {E}}^+$
the associated Weyl chamber, and
${\mathsf {E}}^+$
the associated Weyl chamber, and
![]() ${{{\Phi }}}^+$
and
${{{\Phi }}}^+$
and
![]() ${{{\Delta }}}\subset {{{\Phi }}}$
the corresponding system of positive roots and simple roots, respectively.
${{{\Delta }}}\subset {{{\Phi }}}$
the corresponding system of positive roots and simple roots, respectively.
Let
![]() $\nu :{\mathsf {A}}\to {\mathsf {E}}$
be defined, for
$\nu :{\mathsf {A}}\to {\mathsf {E}}$
be defined, for
![]() $z\in {\mathsf {A}},$
as the unique vector in
$z\in {\mathsf {A}},$
as the unique vector in
![]() ${\mathsf {E}}$
such that for every
${\mathsf {E}}$
such that for every
![]() $\chi \in \mathbf X({\mathsf {A}})$
, one has
$\chi \in \mathbf X({\mathsf {A}})$
, one has
Denote
![]() ${\mathsf {A}}^+=\nu ^{-1}({\mathsf {E}}^+).$
${\mathsf {A}}^+=\nu ^{-1}({\mathsf {E}}^+).$
Let
![]() $\mathcal W$
be the Weyl group of
$\mathcal W$
be the Weyl group of
![]() ${{{\Phi }}}.$
It is isomorphic to the quotient of the normalizer
${{{\Phi }}}.$
It is isomorphic to the quotient of the normalizer
![]() $N_{\mathsf {G}}({\mathsf {A}})$
of
$N_{\mathsf {G}}({\mathsf {A}})$
of
![]() ${\mathsf {A}}$
in
${\mathsf {A}}$
in
![]() ${\mathsf {G}}$
by its centralizer
${\mathsf {G}}$
by its centralizer
![]() $Z_{\mathsf {G}}({\mathsf {A}}).$
Let
$Z_{\mathsf {G}}({\mathsf {A}}).$
Let
![]() $\operatorname {\mathrm {i}}:{\mathsf {E}}\to {\mathsf {E}}$
be the opposition involution: if
$\operatorname {\mathrm {i}}:{\mathsf {E}}\to {\mathsf {E}}$
be the opposition involution: if
![]() $u:{\mathsf {E}}\to {\mathsf {E}}$
is the unique element in the Weyl group with
$u:{\mathsf {E}}\to {\mathsf {E}}$
is the unique element in the Weyl group with
![]() $u({\mathsf {E}}^+)=-{\mathsf {E}}^+$
, then
$u({\mathsf {E}}^+)=-{\mathsf {E}}^+$
, then
![]() $\operatorname {\mathrm {i}}=-u.$
$\operatorname {\mathrm {i}}=-u.$
4.1 Restricted roots and parabolic groups
Consider
![]() $\vartheta \subset {{{\Delta }}}$
and let
$\vartheta \subset {{{\Delta }}}$
and let
![]() ${\mathsf {P}}_\vartheta ,$
respectively
${\mathsf {P}}_\vartheta ,$
respectively
![]() $\check {\mathsf {P}}_\vartheta ,$
be the normalizers in
$\check {\mathsf {P}}_\vartheta ,$
be the normalizers in
![]() ${\mathsf {G}}$
of, respectively the Lie algebras
${\mathsf {G}}$
of, respectively the Lie algebras
 $$ \begin{align*} & \bigoplus_{\alpha\in<{{{\Delta}}}-\vartheta>}{\mathfrak g}_{-\alpha}\oplus \bigoplus_{\alpha\in{{{\Phi}}}^+}{\mathfrak g}_\alpha,\\ & \bigoplus_{\alpha\in<{{{\Delta}}}-\vartheta>}{\mathfrak g}_{\alpha}\oplus \bigoplus_{\alpha\in{{{\Phi}}}^+}{\mathfrak g}_{-\alpha}. \end{align*} $$
$$ \begin{align*} & \bigoplus_{\alpha\in<{{{\Delta}}}-\vartheta>}{\mathfrak g}_{-\alpha}\oplus \bigoplus_{\alpha\in{{{\Phi}}}^+}{\mathfrak g}_\alpha,\\ & \bigoplus_{\alpha\in<{{{\Delta}}}-\vartheta>}{\mathfrak g}_{\alpha}\oplus \bigoplus_{\alpha\in{{{\Phi}}}^+}{\mathfrak g}_{-\alpha}. \end{align*} $$
The
![]() $\vartheta $
-flag space is
$\vartheta $
-flag space is
![]() $\mathcal F_\vartheta ={\mathsf {G}}/{\mathsf {P}}_\vartheta .$
The orbit
$\mathcal F_\vartheta ={\mathsf {G}}/{\mathsf {P}}_\vartheta .$
The orbit
![]() ${\mathsf {G}}\cdot ([\check {\mathsf {P}}_\vartheta ],[{\mathsf {P}}_\vartheta ])\subset \mathcal F_{\operatorname {\mathrm {i}}\vartheta }\times \mathcal F_\vartheta $
is the unique open orbit on this product space, we will denote it by
${\mathsf {G}}\cdot ([\check {\mathsf {P}}_\vartheta ],[{\mathsf {P}}_\vartheta ])\subset \mathcal F_{\operatorname {\mathrm {i}}\vartheta }\times \mathcal F_\vartheta $
is the unique open orbit on this product space, we will denote it by
![]() $\mathcal F^{(2)}_\vartheta $
and say that
$\mathcal F^{(2)}_\vartheta $
and say that
![]() $(x,y)\in \mathcal F_{\operatorname {\mathrm {i}}\vartheta }\times \mathcal F_\vartheta $
are transverse if in fact
$(x,y)\in \mathcal F_{\operatorname {\mathrm {i}}\vartheta }\times \mathcal F_\vartheta $
are transverse if in fact
![]() $(x,y)\in \mathcal F^{(2)}_\vartheta .$
$(x,y)\in \mathcal F^{(2)}_\vartheta .$
Denote by
![]() $(\cdot ,\cdot )$
a
$(\cdot ,\cdot )$
a
![]() $\mathcal W$
-invariant inner product on
$\mathcal W$
-invariant inner product on
![]() ${\mathsf {E}}, (\cdot ,\cdot )$
the induced inner product on
${\mathsf {E}}, (\cdot ,\cdot )$
the induced inner product on
![]() ${\mathsf {E}}^*,$
define
${\mathsf {E}}^*,$
define
![]() $\langle,\rangle $
on
$\langle,\rangle $
on
![]() ${\mathsf {E}}^*$
by
${\mathsf {E}}^*$
by
and let
![]() $\{\varpi _\alpha \}_{\alpha \in \Pi }$
be the fundamental weights of
$\{\varpi _\alpha \}_{\alpha \in \Pi }$
be the fundamental weights of
![]() ${{{\Phi }}},$
defined by the equations
${{{\Phi }}},$
defined by the equations
![]() $\langle\varpi _\alpha ,\sigma\rangle=d_\alpha \delta _{\alpha \sigma },$
where
$\langle\varpi _\alpha ,\sigma\rangle=d_\alpha \delta _{\alpha \sigma },$
where
![]() $d_\alpha =1$
if
$d_\alpha =1$
if
![]() $2\alpha \notin {{{\Phi }}}$
and
$2\alpha \notin {{{\Phi }}}$
and
![]() $d_\alpha =2$
otherwise.
$d_\alpha =2$
otherwise.
4.2 The center of the Levi group
We now consider the vector subspace
together with the unique projection
![]() $p_\vartheta :{\mathsf {E}}\to {\mathsf {E}}_\vartheta $
invariant under the subgroup of the Weyl group
$p_\vartheta :{\mathsf {E}}\to {\mathsf {E}}_\vartheta $
invariant under the subgroup of the Weyl group
![]() $\mathcal W_\vartheta =\{w\in \mathcal W:w|{\mathsf {E}}_\vartheta =\operatorname {\mathrm {id}}\}.$
The dual space
$\mathcal W_\vartheta =\{w\in \mathcal W:w|{\mathsf {E}}_\vartheta =\operatorname {\mathrm {id}}\}.$
The dual space
![]() $({\mathsf {E}}_\vartheta )^*$
sits naturally as the subspace of
$({\mathsf {E}}_\vartheta )^*$
sits naturally as the subspace of
![]() ${\mathsf {E}}^*$
of
${\mathsf {E}}^*$
of
![]() $p_\vartheta $
-invariant linear forms
$p_\vartheta $
-invariant linear forms
It is spanned by the fundamental weights
![]() $\{\varpi _\sigma |{\mathsf {E}}_ \vartheta :\sigma \in \vartheta \}.$
$\{\varpi _\sigma |{\mathsf {E}}_ \vartheta :\sigma \in \vartheta \}.$
4.3 Cartan decomposition
Let
![]() ${\mathsf {K}}\subset {\mathsf {G}}$
be a compact group that contains a representative for every element of the Weyl group
${\mathsf {K}}\subset {\mathsf {G}}$
be a compact group that contains a representative for every element of the Weyl group
![]() $\mathcal W,$
this is to say, such that the normalizer
$\mathcal W,$
this is to say, such that the normalizer
![]() $N_{\mathsf {G}}({\mathsf {A}})$
verifies
$N_{\mathsf {G}}({\mathsf {A}})$
verifies
![]() $N_{\mathsf {G}}({\mathsf {A}})=(N_{\mathsf { G}}({\mathsf {A}})\cap {\mathsf {K}}){\mathsf {A}}.$
One has
$N_{\mathsf {G}}({\mathsf {A}})=(N_{\mathsf { G}}({\mathsf {A}})\cap {\mathsf {K}}){\mathsf {A}}.$
One has
![]() ${\mathsf {G}}={\mathsf {K}}{\mathsf {A}}^+{\mathsf {K}}$
and if
${\mathsf {G}}={\mathsf {K}}{\mathsf {A}}^+{\mathsf {K}}$
and if
![]() $z,w\in {\mathsf {A}}^+$
are such that
$z,w\in {\mathsf {A}}^+$
are such that
![]() $z\in {\mathsf {K}}w{\mathsf {K}}$
, then
$z\in {\mathsf {K}}w{\mathsf {K}}$
, then
![]() $\nu (z)=\nu (w).$
There exists thus a function
$\nu (z)=\nu (w).$
There exists thus a function
such that for every
![]() $g_1,g_2\in {\mathsf {G}}$
, one has
$g_1,g_2\in {\mathsf {G}}$
, one has
![]() $g_1\in {\mathsf {K}}g_2 {\mathsf {K}}$
if and only if
$g_1\in {\mathsf {K}}g_2 {\mathsf {K}}$
if and only if
![]() $a(g_1)=a(g_2).$
It is called the Cartan projection of
$a(g_1)=a(g_2).$
It is called the Cartan projection of
![]() ${\mathsf {G}}.$
${\mathsf {G}}.$
4.4 Jordan decomposition
Recall that the Jordan decomposition states that every
![]() $g\in {\mathsf {G}}$
has a power
$g\in {\mathsf {G}}$
has a power
![]() $g^k$
(
$g^k$
(
![]() $k=1$
if
$k=1$
if
![]() $\mathbb {K}$
is Archimedean) that can be written as a commuting product
$\mathbb {K}$
is Archimedean) that can be written as a commuting product
![]() $g=g_eg_hg_n,$
where
$g=g_eg_hg_n,$
where
![]() $g_e$
is elliptic,
$g_e$
is elliptic,
![]() $g_h$
is semi-simple over
$g_h$
is semi-simple over
![]() $\mathbb {K}$
, and
$\mathbb {K}$
, and
![]() $g_n$
is unipotent. The component
$g_n$
is unipotent. The component
![]() $g_h$
is conjugate to an element
$g_h$
is conjugate to an element
![]() $z_g\in {\mathsf {A}}^+$
and we let
$z_g\in {\mathsf {A}}^+$
and we let
The map
![]() $\unicode{x3bb} :{\mathsf {G}}\to {\mathsf {E}}^+$
is the Jordan projection of
$\unicode{x3bb} :{\mathsf {G}}\to {\mathsf {E}}^+$
is the Jordan projection of
![]() ${\mathsf {G}}.$
We will also denote by
${\mathsf {G}}.$
We will also denote by
![]() $\unicode{x3bb} _\vartheta :{\mathsf {G}}\to {\mathsf {E}}_\vartheta $
the composition
$\unicode{x3bb} _\vartheta :{\mathsf {G}}\to {\mathsf {E}}_\vartheta $
the composition
![]() $p_\vartheta \circ \unicode{x3bb} .$
For
$p_\vartheta \circ \unicode{x3bb} .$
For
![]() ${\mathsf {G}}=\operatorname {\mathrm {{\mathsf {PGL}}}}_d(\mathbb {K})$
, we will denote by
${\mathsf {G}}=\operatorname {\mathrm {{\mathsf {PGL}}}}_d(\mathbb {K})$
, we will denote by
![]() $\unicode{x3bb} _1(g)$
the logarithm of the spectral radius of
$\unicode{x3bb} _1(g)$
the logarithm of the spectral radius of
![]() $g.$
$g.$
4.5 Representations of
 ${\mathsf {G}}$
${\mathsf {G}}$
Let
![]() ${\mathsf {V}}$
be a finite-dimensional
${\mathsf {V}}$
be a finite-dimensional
![]() $\mathbb {K}$
-vector space and
$\mathbb {K}$
-vector space and
![]() $\unicode{x3c6} :{\mathsf {G}}\to \operatorname {\mathrm {{\mathsf {PGL}}}}({\mathsf {V}})$
be an algebraic irreducible representation. Then the weight space associated to
$\unicode{x3c6} :{\mathsf {G}}\to \operatorname {\mathrm {{\mathsf {PGL}}}}({\mathsf {V}})$
be an algebraic irreducible representation. Then the weight space associated to
![]() $\chi \in \mathbf X({\mathsf {A}})$
is the vector space
$\chi \in \mathbf X({\mathsf {A}})$
is the vector space
and if
![]() $V_\chi \neq 0$
, then we say that
$V_\chi \neq 0$
, then we say that
![]() $\chi ^\omega \in {\mathsf {E}}^*$
is a restricted weight of
$\chi ^\omega \in {\mathsf {E}}^*$
is a restricted weight of
![]() $\unicode{x3c6} .$
Theorem 7.2 of Tits [Reference Tits69] states that the set of weights has a unique maximal element with respect to the order
$\unicode{x3c6} .$
Theorem 7.2 of Tits [Reference Tits69] states that the set of weights has a unique maximal element with respect to the order
![]() $\chi \geq \psi $
if
$\chi \geq \psi $
if
![]() $\chi -\psi $
is a sum of simple roots with non-negative coefficients. This is called the highest weight of
$\chi -\psi $
is a sum of simple roots with non-negative coefficients. This is called the highest weight of
![]() $\unicode{x3c6} $
and denoted by
$\unicode{x3c6} $
and denoted by
![]() $\chi _\unicode{x3c6} .$
$\chi _\unicode{x3c6} .$
We denote by
![]() $\|\,\|_\unicode{x3c6} $
a norm on
$\|\,\|_\unicode{x3c6} $
a norm on
![]() ${\mathsf {V}}$
invariant under
${\mathsf {V}}$
invariant under
![]() $\unicode{x3c6} {\mathsf {K}}$
and such that
$\unicode{x3c6} {\mathsf {K}}$
and such that
![]() $\unicode{x3c6} {\mathsf {A}}$
consists on semi-homotheties (that is, diagonal on an orthonormal basis
$\unicode{x3c6} {\mathsf {A}}$
consists on semi-homotheties (that is, diagonal on an orthonormal basis
![]() $\mathcal E$
of
$\mathcal E$
of
![]() $V,$
in the classical sense if
$V,$
in the classical sense if
![]() $\mathbb {K}$
Archimedean, and such that
$\mathbb {K}$
Archimedean, and such that
![]() $\|\sum _{e\in \mathcal E}v_ee\|=\max \{|v_e|\}$
if
$\|\sum _{e\in \mathcal E}v_ee\|=\max \{|v_e|\}$
if
![]() $\mathbb {K}$
is non-Archimedean). If
$\mathbb {K}$
is non-Archimedean). If
![]() $\mathbb {K}$
is Archimedean, the existence of such a norm is classical (see for example [Reference Benoist and Quint9, Lemma 6.33]), if
$\mathbb {K}$
is Archimedean, the existence of such a norm is classical (see for example [Reference Benoist and Quint9, Lemma 6.33]), if
![]() $\mathbb {K}$
is non-Archimedean, then this is the content of [Reference Quint60, Théorème 6.1] due to Quint.
$\mathbb {K}$
is non-Archimedean, then this is the content of [Reference Quint60, Théorème 6.1] due to Quint.
For every
![]() $g\in {\mathsf {G}}$
, one has then
$g\in {\mathsf {G}}$
, one has then

Denote by
![]() $W_{\chi _\unicode{x3c6} }$
the
$W_{\chi _\unicode{x3c6} }$
the
![]() $\unicode{x3c6} {\mathsf {A}}$
-invariant complement of
$\unicode{x3c6} {\mathsf {A}}$
-invariant complement of
![]() ${\mathsf {V}}_{\chi _\unicode{x3c6} }.$
The stabilizer in
${\mathsf {V}}_{\chi _\unicode{x3c6} }.$
The stabilizer in
![]() ${\mathsf {G}}$
of
${\mathsf {G}}$
of
![]() ${\mathsf {W}}_{\chi _\unicode{x3c6} }$
is
${\mathsf {W}}_{\chi _\unicode{x3c6} }$
is
![]() $\check {\mathsf {P}}_{\vartheta ,\mathbb {K}},$
and thus one has a map of flag spaces
$\check {\mathsf {P}}_{\vartheta ,\mathbb {K}},$
and thus one has a map of flag spaces
where
![]() $\vartheta _\unicode{x3c6} =\{\sigma \in {{{\Delta }}}:\chi _\unicode{x3c6} -\sigma \textrm { is a weight of }\unicode{x3c6} \}$
. This is a proper embedding which is a homeomorphism onto its image. Here,
$\vartheta _\unicode{x3c6} =\{\sigma \in {{{\Delta }}}:\chi _\unicode{x3c6} -\sigma \textrm { is a weight of }\unicode{x3c6} \}$
. This is a proper embedding which is a homeomorphism onto its image. Here,
![]() $\mathscr G_{\dim {\mathsf {V}}_{\chi _\unicode{x3c6} }}^{(2)}({\mathsf {V}})$
is the open
$\mathscr G_{\dim {\mathsf {V}}_{\chi _\unicode{x3c6} }}^{(2)}({\mathsf {V}})$
is the open
![]() $\operatorname {\mathrm {{\mathsf {PGL}}}} ({\mathsf {V}})$
-orbit in the product of the Grassmannians of
$\operatorname {\mathrm {{\mathsf {PGL}}}} ({\mathsf {V}})$
-orbit in the product of the Grassmannians of
![]() $(\dim {\mathsf {V}}_{\chi _\unicode{x3c6} })$
-dimensional and
$(\dim {\mathsf {V}}_{\chi _\unicode{x3c6} })$
-dimensional and
![]() $(\dim {\mathsf {V}}-\dim {\mathsf {V}}_{\chi _\unicode{x3c6} })$
-dimensional subspaces.
$(\dim {\mathsf {V}}-\dim {\mathsf {V}}_{\chi _\unicode{x3c6} })$
-dimensional subspaces.
One has the following proposition from Tits [Reference Tits69] that guarantees existence of certain representations of
![]() ${\mathsf {G}}.$
We say that
${\mathsf {G}}.$
We say that
![]() $\phi $
is proximal if
$\phi $
is proximal if
![]() $\dim {\mathsf {V}}_{\chi _\unicode{x3c6} }=1.$
$\dim {\mathsf {V}}_{\chi _\unicode{x3c6} }=1.$
Proposition 4.5.1. (Tits [Reference Tits69])
For every
![]() $\sigma \in {{{\Delta }}}$
, there exists an irreducible proximal representation of
$\sigma \in {{{\Delta }}}$
, there exists an irreducible proximal representation of
![]() ${\mathsf {G}}$
whose highest restricted weight is
${\mathsf {G}}$
whose highest restricted weight is
![]() $l_\sigma \varpi _\sigma $
for some
$l_\sigma \varpi _\sigma $
for some
![]() $l_\sigma \in \mathbb {Z}_{\geq 1}.$
$l_\sigma \in \mathbb {Z}_{\geq 1}.$
Definition 4.5.2. We will fix and denote by
![]() $\unicode{x3c6} _\sigma :{\mathsf {G}}\to \operatorname {\mathrm {{\mathsf {GL}}}}({\mathsf {V}}_\sigma )$
such a set of representations.
$\unicode{x3c6} _\sigma :{\mathsf {G}}\to \operatorname {\mathrm {{\mathsf {GL}}}}({\mathsf {V}}_\sigma )$
such a set of representations.
4.6 Buseman–Iwasawa cocycle
The Iwasawa decomposition of
![]() ${\mathsf {G}}$
states that every
${\mathsf {G}}$
states that every
![]() $g\in {\mathsf {G}}$
can be written as a product
$g\in {\mathsf {G}}$
can be written as a product
![]() $lzu$
with
$lzu$
with
![]() $l\in {\mathsf {K}}, z\in {\mathsf {A}}$
, and
$l\in {\mathsf {K}}, z\in {\mathsf {A}}$
, and
![]() $u\in {\mathsf {U}}_{{{\Delta }}},$
where
$u\in {\mathsf {U}}_{{{\Delta }}},$
where
![]() ${\mathsf {U}}_{{{\Delta }}}$
is the unipotent radical of
${\mathsf {U}}_{{{\Delta }}}$
is the unipotent radical of
![]() ${\mathsf {P}}_{{{{\Delta }}}}.$
When
${\mathsf {P}}_{{{{\Delta }}}}.$
When
![]() $\mathbb {K}$
is non-Archimedean, the Iwasawa decomposition is not unique; however, if
$\mathbb {K}$
is non-Archimedean, the Iwasawa decomposition is not unique; however, if
![]() $z_1,z_2\in {\mathsf {A}}$
are such that
$z_1,z_2\in {\mathsf {A}}$
are such that
![]() $z_1\in {\mathsf {K}} z_2{\mathsf {U}}_{{{{\Delta }}}}$
, then
$z_1\in {\mathsf {K}} z_2{\mathsf {U}}_{{{{\Delta }}}}$
, then
![]() $\nu (z_1)=\nu (z_2).$
$\nu (z_1)=\nu (z_2).$
The Buseman–Iwasawa cocycle of
![]() ${\mathsf {G}}, \beta :{\mathsf {G}}\times \mathcal F\to {\mathsf {E}},$
is defined, for all
${\mathsf {G}}, \beta :{\mathsf {G}}\times \mathcal F\to {\mathsf {E}},$
is defined, for all
![]() $g\in {\mathsf {G}}$
and
$g\in {\mathsf {G}}$
and
![]() $k[{\mathsf {P}}_{{{\Delta }}}]\in \mathcal F,$
if
$k[{\mathsf {P}}_{{{\Delta }}}]\in \mathcal F,$
if
![]() $gk=lzu$
is an Iwasawa decomposition of
$gk=lzu$
is an Iwasawa decomposition of
![]() $gk$
, by
$gk$
, by
![]() $\beta (g,k[{\mathsf {P}}_{{{\Delta }}}])=\nu (z).$
Quint proved the following lemma.
$\beta (g,k[{\mathsf {P}}_{{{\Delta }}}])=\nu (z).$
Quint proved the following lemma.
Lemma 4.6.1. (Quint [Reference Quint62, Lemmas 6.1 and 6.2])
The function
![]() $\beta _\vartheta =p_\vartheta \circ \beta $
factors as a cocycle
$\beta _\vartheta =p_\vartheta \circ \beta $
factors as a cocycle
![]() $\beta _\vartheta :{\mathsf {G}}\times \mathcal F_\vartheta \to {\mathsf {E}}_\vartheta .$
$\beta _\vartheta :{\mathsf {G}}\times \mathcal F_\vartheta \to {\mathsf {E}}_\vartheta .$
The Buseman–Iwasawa cocycle can also be read from the representations of
![]() ${\mathsf {G}}.$
Indeed, Quint [Reference Quint62, Lemme 6.4] states that for every
${\mathsf {G}}.$
Indeed, Quint [Reference Quint62, Lemme 6.4] states that for every
![]() $g\in {\mathsf {G}}$
and
$g\in {\mathsf {G}}$
and
![]() $x\in \mathcal F_\vartheta $
, one has
$x\in \mathcal F_\vartheta $
, one has

where
![]() $v\in \Xi _{\unicode{x3c6} _\sigma }(x)\in \mathbb {P}({\mathsf {V}}_\sigma )$
is non-zero.
$v\in \Xi _{\unicode{x3c6} _\sigma }(x)\in \mathbb {P}({\mathsf {V}}_\sigma )$
is non-zero.
4.7 Gromov product
As in [Reference Sambarino66], the Gromov product
![]() $\mathscr G_\vartheta :\mathcal F^{(2)}_\vartheta \to {\mathsf {E}}_\vartheta $
is defined such that, for every
$\mathscr G_\vartheta :\mathcal F^{(2)}_\vartheta \to {\mathsf {E}}_\vartheta $
is defined such that, for every
![]() $(x,y)\in \mathcal F^{(2)}_\vartheta $
and
$(x,y)\in \mathcal F^{(2)}_\vartheta $
and
![]() $\sigma \in \vartheta ,$
one has
$\sigma \in \vartheta ,$
one has

where
![]() $\varphi \in \Xi ^*_{\unicode{x3c6} _\sigma }(x)$
and
$\varphi \in \Xi ^*_{\unicode{x3c6} _\sigma }(x)$
and
![]() $v\in \Xi _{\unicode{x3c6} _\sigma }(y)$
are the equivariant maps from equation (20).
$v\in \Xi _{\unicode{x3c6} _\sigma }(y)$
are the equivariant maps from equation (20).
Remark 4.7.1. Observe that the limiting situation
![]() $l_\sigma \varpi _\sigma (\mathscr G_\vartheta (x,y))=-\infty $
occurs when
$l_\sigma \varpi _\sigma (\mathscr G_\vartheta (x,y))=-\infty $
occurs when
![]() $v\in \ker \varphi ,$
that is, when x and y are no longer transverse flags, so a statement of the form
$v\in \ker \varphi ,$
that is, when x and y are no longer transverse flags, so a statement of the form
![]() $\varpi _\sigma \mathscr G_\vartheta (x,y) \geq -\kappa $
for all
$\varpi _\sigma \mathscr G_\vartheta (x,y) \geq -\kappa $
for all
![]() $\sigma \in \vartheta $
is a quantitative version (that depends on
$\sigma \in \vartheta $
is a quantitative version (that depends on
![]() ${\mathsf {K}}$
) of the transversality between x and
${\mathsf {K}}$
) of the transversality between x and
![]() $y.$
$y.$
A straightforward computation ([Reference Sambarino66, Lemma 4.12]) gives, for all
![]() $g{\kern-1.5pt}\in{\kern-1.5pt} {\mathsf {G}}$
and
$g{\kern-1.5pt}\in{\kern-1.5pt} {\mathsf {G}}$
and
![]() $(x,{\kern-1pt}y){\kern-1.5pt}\in{\kern-1.5pt} \mathcal F^{(2)}_\vartheta ,$
$(x,{\kern-1pt}y){\kern-1.5pt}\in{\kern-1.5pt} \mathcal F^{(2)}_\vartheta ,$
4.8 Proximality
Recall that
![]() $g\in \operatorname {\mathrm {{\mathsf {PGL}}}}_d({\mathsf {V}})$
is proximal if it has a unique eigenvalue with maximal modulus and that the multiplicity of this eigenvalue in the characteristic polynomial of g is
$g\in \operatorname {\mathrm {{\mathsf {PGL}}}}_d({\mathsf {V}})$
is proximal if it has a unique eigenvalue with maximal modulus and that the multiplicity of this eigenvalue in the characteristic polynomial of g is
![]() $1.$
The associated eigenline is denoted by
$1.$
The associated eigenline is denoted by
![]() $g^+\in \mathbb {P}({\mathsf {V}})$
and
$g^+\in \mathbb {P}({\mathsf {V}})$
and
![]() $g^-$
is its g-invariant complementary subspace.
$g^-$
is its g-invariant complementary subspace.
We say then that
![]() $g\in {\mathsf {G}}$
is
$g\in {\mathsf {G}}$
is
![]() $\vartheta $
-proximal if for every
$\vartheta $
-proximal if for every
![]() $\sigma \in \vartheta $
, one has
$\sigma \in \vartheta $
, one has
![]() $\unicode{x3c6} _\sigma (g)$
is proximal. In this situation, there exists a pair
$\unicode{x3c6} _\sigma (g)$
is proximal. In this situation, there exists a pair
![]() $(g^-_\vartheta ,g^+_\vartheta )\in \mathcal F^{(2)}_\vartheta ,$
defined by, for every
$(g^-_\vartheta ,g^+_\vartheta )\in \mathcal F^{(2)}_\vartheta ,$
defined by, for every
![]() $\sigma \in \vartheta , \Xi _{\unicode{x3c6} _\sigma }(g^+_\vartheta )=\unicode{x3c6} _\sigma (g)^+,$
and every flag
$\sigma \in \vartheta , \Xi _{\unicode{x3c6} _\sigma }(g^+_\vartheta )=\unicode{x3c6} _\sigma (g)^+,$
and every flag
![]() $x\in \mathcal F_\vartheta $
in general position with
$x\in \mathcal F_\vartheta $
in general position with
![]() $g^-_\vartheta $
verifies
$g^-_\vartheta $
verifies
![]() $g^nx\to g^+_\vartheta .$
$g^nx\to g^+_\vartheta .$
It is also useful to consider a quantified version of proximality. Given
![]() $r,\varepsilon $
positive, we say that g is
$r,\varepsilon $
positive, we say that g is
![]() $(r,\varepsilon )$
-proximal if it is proximal,
$(r,\varepsilon )$
-proximal if it is proximal,
for all
![]() $\sigma \in \vartheta $
, and for every
$\sigma \in \vartheta $
, and for every
![]() $x\in \mathcal F_\vartheta $
with
$x\in \mathcal F_\vartheta $
with
![]() $\min _{\sigma _\in \vartheta }\varpi _\sigma \mathscr G_\vartheta (g_\vartheta ^-,x)\geq - \varepsilon ^{-1}$
, one has
$\min _{\sigma _\in \vartheta }\varpi _\sigma \mathscr G_\vartheta (g_\vartheta ^-,x)\geq - \varepsilon ^{-1}$
, one has
![]() $d_{\mathcal F_\vartheta }(gx,g^+_\vartheta )\leq \varepsilon .$
More details on the following can be found in [Reference Sambarino65, Lemma 5.6].
$d_{\mathcal F_\vartheta }(gx,g^+_\vartheta )\leq \varepsilon .$
More details on the following can be found in [Reference Sambarino65, Lemma 5.6].
Proposition 4.8.1. (Benoist [Reference Benoist6, Corollaire 6.3])
For every
![]() $\delta>0$
, there exist
$\delta>0$
, there exist
![]() $r,\varepsilon>0$
such that if
$r,\varepsilon>0$
such that if
![]() $g\in {\mathsf {G}}$
is
$g\in {\mathsf {G}}$
is
![]() $(r,\varepsilon )$
-proximal, then
$(r,\varepsilon )$
-proximal, then
4.9 Cartan attractors
Consider
![]() $g\in {\mathsf {G}}$
and let
$g\in {\mathsf {G}}$
and let
![]() $g=k_gz_gl_g$
be a Cartan decomposition. We say that
$g=k_gz_gl_g$
be a Cartan decomposition. We say that
![]() $g\in {\mathsf {G}}$
has a gap at
$g\in {\mathsf {G}}$
has a gap at
![]() $\vartheta $
if for all
$\vartheta $
if for all
![]() $\sigma \in \vartheta $
, one has
$\sigma \in \vartheta $
, one has
In that case, the Cartan attractor of g in
![]() $\mathcal F_\vartheta $
$\mathcal F_\vartheta $
is well defined: uniquely defined if
![]() $\mathbb {K}$
is Archimedian; defined up to a ball of radius
$\mathbb {K}$
is Archimedian; defined up to a ball of radius
![]() $q^{-\min _{\sigma \in \vartheta }\sigma (g)}$
if
$q^{-\min _{\sigma \in \vartheta }\sigma (g)}$
if
![]() $\mathbb {K}$
is non-Archimedean (see [Reference Pozzetti, Sambarino and Wienhard59, Remark 2.4]).
$\mathbb {K}$
is non-Archimedean (see [Reference Pozzetti, Sambarino and Wienhard59, Remark 2.4]).
Remark 4.9.1. For every
![]() $\sigma \in \vartheta $
, one has
$\sigma \in \vartheta $
, one has
![]() ${\displaystyle \Xi _{\unicode{x3c6} _\sigma }(U_\vartheta (g))=U_{1}(\unicode{x3c6} _\sigma (g)).}$
${\displaystyle \Xi _{\unicode{x3c6} _\sigma }(U_\vartheta (g))=U_{1}(\unicode{x3c6} _\sigma (g)).}$
Lemma 4.9.2. (Bochi, Potrie, and Sambarino [Reference Bochi, Potrie and Sambarino10, Lemma A.5])
Consider
![]() $g,h\in {\mathsf {G}}$
such that h and
$g,h\in {\mathsf {G}}$
such that h and
![]() $gh$
have gaps at every
$gh$
have gaps at every
![]() $\sigma \in \vartheta ,$
then one has
$\sigma \in \vartheta ,$
then one has
The Cartan basin of g is defined, for
![]() $\alpha>0,$
by (recall Remark 4.7.1)
$\alpha>0,$
by (recall Remark 4.7.1)
It is clear from the definition that given
![]() $\alpha>0$
, there exists a constant
$\alpha>0$
, there exists a constant
![]() $K_\alpha $
such that if
$K_\alpha $
such that if
![]() $y\in \mathcal F_{\vartheta }$
belongs to
$y\in \mathcal F_{\vartheta }$
belongs to
![]() $B_{\vartheta ,\alpha }(g)$
, then one has
$B_{\vartheta ,\alpha }(g)$
, then one has
Lemma 4.9.3. (Quint [Reference Quint62, Lemme 6.6])
For every
![]() $g\in {\mathsf {G}}$
, one has
$g\in {\mathsf {G}}$
, one has
![]() $a_\vartheta (gh)-a_\vartheta (h)-\beta _\vartheta (g,U_\vartheta (h))\to 0$
as
$a_\vartheta (gh)-a_\vartheta (h)-\beta _\vartheta (g,U_\vartheta (h))\to 0$
as
![]() $\min _{\sigma \in \vartheta }\sigma (a(h))\to \infty .$
$\min _{\sigma \in \vartheta }\sigma (a(h))\to \infty .$
4.10 General facts on discrete subgroups
We record here some facts related to the title that we will need in the following work.
Lemma 4.10.1. Let
![]() $\Delta \subset {\mathsf {G}}$
be a discrete subgroup. Then for every
$\Delta \subset {\mathsf {G}}$
be a discrete subgroup. Then for every
![]() $\varphi \in {\mathsf {E}}^*$
strictly positive on
$\varphi \in {\mathsf {E}}^*$
strictly positive on
![]() ${\mathsf {E}}^+$
, the exponential rate
${\mathsf {E}}^+$
, the exponential rate
is finite.
Proof. The proof follows from a computation of the Haar measure of
![]() ${\mathsf {G}},$
to be found in [Reference Helgason37] for the Archimedean case and in [Reference Matsumoto50, §3.2.7] for the non-Archimedean case, see [Reference Quint61, §4] for details.
${\mathsf {G}},$
to be found in [Reference Helgason37] for the Archimedean case and in [Reference Matsumoto50, §3.2.7] for the non-Archimedean case, see [Reference Quint61, §4] for details.
We record also the following theorem from Benoist [Reference Benoist8].
Theorem 4.10.2. (Benoist [Reference Benoist8])
Assume
![]() $\mathbb {K}=\mathbb {R}$
and let
$\mathbb {K}=\mathbb {R}$
and let
![]() $\Delta \subset {\mathsf {G}}$
be a Zariski-dense subgroup. Then, the group spanned by the Jordan projections
$\Delta \subset {\mathsf {G}}$
be a Zariski-dense subgroup. Then, the group spanned by the Jordan projections
![]() $\{\unicode{x3bb} (g):g\in \Delta \}$
is dense in
$\{\unicode{x3bb} (g):g\in \Delta \}$
is dense in
![]() ${\mathsf {E}}.$
${\mathsf {E}}.$
5 Anosov representations
Anosov representations were introduced by Labourie [Reference Labourie43] for fundamental groups of negatively curved manifolds and extended to arbitrary finitely generated hyperbolic groups by Guichard and Wienhard [Reference Guichard and Wienhard35]. They originated as a tool to study higher rank Teichmüller theory, and are nowadays considered as the higher-rank analog of what is known in pinched negative curvature as convex co-compact groups.
Notation. If
![]() is a representation, we will simplify notation and denote, for
is a representation, we will simplify notation and denote, for
![]() by
by
![]() $\gamma _\rho =\rho (\gamma ).$
$\gamma _\rho =\rho (\gamma ).$
5.1 Real projective-Anosov representations
We begin by recalling Labourie’s original approach. Let
![]() be a finitely generated word-hyperbolic group. If
be a finitely generated word-hyperbolic group. If
![]() is a representation, then we can consider the natural flat bundle automorphism defined as follows. Consider the flat bundle
is a representation, then we can consider the natural flat bundle automorphism defined as follows. Consider the flat bundle
![]() defined by
defined by
![]() , where
, where
![]() $(p,v)\sim (\gamma p,\gamma _\rho v),$
and define
$(p,v)\sim (\gamma p,\gamma _\rho v),$
and define
![]() $\hat {\mathsf {g}}=(\hat {\mathsf {g}}_t:{\mathsf {E}}_\rho \to {\mathsf {E}}_\rho )_{t\in \mathbb {R}}$
as the induction on the quotient by
$\hat {\mathsf {g}}=(\hat {\mathsf {g}}_t:{\mathsf {E}}_\rho \to {\mathsf {E}}_\rho )_{t\in \mathbb {R}}$
as the induction on the quotient by
![]() $t\cdot (p,v)=(\widetilde {\mathsf {g}}_t p, v).$
$t\cdot (p,v)=(\widetilde {\mathsf {g}}_t p, v).$
Definition 5.1.1. The representation
![]() $\rho $
is projective-Anosov if there exists a pair of continuous
$\rho $
is projective-Anosov if there exists a pair of continuous
![]() $\rho $
-equivariant maps
$\rho $
-equivariant maps

such that:
-
• for every
 , one has
, one has
 $\ker \xi ^{d-1}(x)\oplus \xi ^1(y)=\mathbb {R}^d.$
This induces a
$\ker \xi ^{d-1}(x)\oplus \xi ^1(y)=\mathbb {R}^d.$
This induces a
 $\hat {\mathsf {g}}$
-invariant decomposition
$\hat {\mathsf {g}}$
-invariant decomposition
 $\Xi \oplus \Theta ={\mathsf {E}}_\rho $
;
$\Xi \oplus \Theta ={\mathsf {E}}_\rho $
; -
• the decomposition
 ${\mathsf {E}}_\rho =\Xi \oplus \Theta $
is a dominated splitting for
${\mathsf {E}}_\rho =\Xi \oplus \Theta $
is a dominated splitting for
 $\hat {\mathsf {g}},$
that is, there exist
$\hat {\mathsf {g}},$
that is, there exist
 $c,\alpha $
positive such that for every
$c,\alpha $
positive such that for every
 $v\in \Xi _p$
and
$v\in \Xi _p$
and
 $w\in \Theta _p$
, one has
$w\in \Theta _p$
, one has  $$ \begin{align*}\frac{\|\hat{\mathsf{g}}_tv\|}{\|\hat{\mathsf{g}}_tw\|}\leq ce^{-\alpha t}\frac{\|v\|}{\|w\|}.\end{align*} $$
$$ \begin{align*}\frac{\|\hat{\mathsf{g}}_tv\|}{\|\hat{\mathsf{g}}_tw\|}\leq ce^{-\alpha t}\frac{\|v\|}{\|w\|}.\end{align*} $$
One has the following standard consequences, see for example [Reference Guichard and Wienhard35, Lemma 3.1] or [Reference Bridgeman, Canary, Labourie and Sambarino17, Lemma 2.5 and Proposition 2.6]. Recall from §4.8 that
![]() $g\in \operatorname {\mathrm {{\mathsf {PGL}}}}_d(\mathbb {R})$
is proximal if the Jordan block associated to the eigenvalues with maximal modulus is one-dimensional.
$g\in \operatorname {\mathrm {{\mathsf {PGL}}}}_d(\mathbb {R})$
is proximal if the Jordan block associated to the eigenvalues with maximal modulus is one-dimensional.
Lemma 5.1.2. If
![]() $\rho $
is projective-Anosov, then for every hyperbolic
$\rho $
is projective-Anosov, then for every hyperbolic
![]() $\gamma $
, one has
$\gamma $
, one has
![]() $\gamma _\rho $
is proximal with attracting line
$\gamma _\rho $
is proximal with attracting line
![]() $\xi ^1(\gamma _+).$
In particular, the entropy
$\xi ^1(\gamma _+).$
In particular, the entropy
The equivariant maps
![]() $\xi ^1$
and
$\xi ^1$
and
![]() $\xi ^{d-1}$
are Hölder-continuous.
$\xi ^{d-1}$
are Hölder-continuous.
Proof. Let us add a word on finiteness of entropy. Recall from Bowditch [Reference Bowditch13] that, since
is hyperbolic, its action on the space of pairwise distinct triples
is properly discontinuous and co-compact. If
is hyperbolic, one can choose then
![]() $\eta \in [\gamma ]$
(the conjugacy class of
$\eta \in [\gamma ]$
(the conjugacy class of
![]() $\gamma $
) whose fixed points are far apart by a constant independent of
$\gamma $
) whose fixed points are far apart by a constant independent of
![]() $\gamma .$
Since the image
$\gamma .$
Since the image
![]() $\gamma _\rho $
is proximal and the equivariant maps are continuous, one has that
$\gamma _\rho $
is proximal and the equivariant maps are continuous, one has that
![]() $\eta _\rho $
is
$\eta _\rho $
is
![]() $(r,\varepsilon )$
-proximal for constants
$(r,\varepsilon )$
-proximal for constants
![]() $r,\varepsilon $
independent of
$r,\varepsilon $
independent of
![]() $[\gamma ].$
By Proposition 4.8.1, one has then
$[\gamma ].$
By Proposition 4.8.1, one has then
![]() $|\log \|\eta _\rho \|-\unicode{x3bb} _1(\eta _\rho )|<K$
for some K independent of
$|\log \|\eta _\rho \|-\unicode{x3bb} _1(\eta _\rho )|<K$
for some K independent of
![]() $\eta .$
If follows then that for every
$\eta .$
If follows then that for every
![]() $t\in \mathbb {R}_+$
,
$t\in \mathbb {R}_+$
,
Finiteness of entropy then follows from Lemma 4.10.1.
We use the equivariant maps to construct a bundle
![]() whose fiber at
whose fiber at
![]() is
is
where
![]() $(\varphi ,v)\sim (-\varphi ,-v).$
This bundle is equipped with a
$(\varphi ,v)\sim (-\varphi ,-v).$
This bundle is equipped with a
![]() -action
-action
![]() $\gamma (\varphi ,v)= (\varphi \circ \gamma ^{-1}_\rho ,\gamma _\rho v)$
and an
$\gamma (\varphi ,v)= (\varphi \circ \gamma ^{-1}_\rho ,\gamma _\rho v)$
and an
![]() $\mathbb {R}$
-action
$\mathbb {R}$
-action
![]() $(\widetilde {\mathsf {g^\rho }}_t:\widetilde {\mathsf {F}}\to \widetilde {\mathsf {F}})_{t\in \mathbb {R}}$
defined by
$(\widetilde {\mathsf {g^\rho }}_t:\widetilde {\mathsf {F}}\to \widetilde {\mathsf {F}})_{t\in \mathbb {R}}$
defined by
![]() $\widetilde {\mathsf {g^\rho }}_t\cdot (\varphi ,v)=(e^t\varphi ,e^{-t}v).$
Let
$\widetilde {\mathsf {g^\rho }}_t\cdot (\varphi ,v)=(e^t\varphi ,e^{-t}v).$
Let
![]() and denote by
and denote by
![]() ${\mathsf {g}}^\rho =({\mathsf {g}}^\rho _t:{\mathsf {F}}\to {\mathsf {F}})_{t\in \mathbb {R}}$
the induced flow on the quotient. It is usually called the geodesic flow of
${\mathsf {g}}^\rho =({\mathsf {g}}^\rho _t:{\mathsf {F}}\to {\mathsf {F}})_{t\in \mathbb {R}}$
the induced flow on the quotient. It is usually called the geodesic flow of
![]() $\rho $
.
$\rho $
.
Theorem 5.1.3. (Bridgeman et al [Reference Bridgeman, Canary, Labourie and Sambarino17])
The above
![]() -action is properly discontinuous and co-compact. The flow
-action is properly discontinuous and co-compact. The flow
![]() ${\mathsf {g}}^\rho $
is Hölder-continuous and metric-Anosov with stable/unstable laminations (induced on the quotient by)
${\mathsf {g}}^\rho $
is Hölder-continuous and metric-Anosov with stable/unstable laminations (induced on the quotient by)
 $$ \begin{align*}\tilde W^{\mathrm{s}}((x,y,(\varphi,v)) & =\{(x,\cdot,(\varphi,\cdot))\in\widetilde{\mathsf{F}}\},\\ W^{{\mathrm{u}}}((x,y,(\varphi,v)) & =\{(\cdot,y,(\cdot,v))\in\widetilde{\mathsf{F}}\}.\end{align*} $$
$$ \begin{align*}\tilde W^{\mathrm{s}}((x,y,(\varphi,v)) & =\{(x,\cdot,(\varphi,\cdot))\in\widetilde{\mathsf{F}}\},\\ W^{{\mathrm{u}}}((x,y,(\varphi,v)) & =\{(\cdot,y,(\cdot,v))\in\widetilde{\mathsf{F}}\}.\end{align*} $$
It is moreover Hölder-conjugated to the Gromov–Mineyev geodesic flow
![]() ${\mathsf {g}}$
of
${\mathsf {g}}$
of
![]() consequently, this latter flow is also metric-Anosov.
consequently, this latter flow is also metric-Anosov.
Therefore, hyperbolic groups admitting a real projective-Anosov representation verify Assumption B and are thus subject of a Ledrappier correspondence (§3). It is established by Carvajales [Reference Carvajales22, Appendix] that
![]() ${\mathsf {g}}^\rho $
is topologically mixing (regardless of the Zariski closure of
${\mathsf {g}}^\rho $
is topologically mixing (regardless of the Zariski closure of
![]() $\rho $
) and thus mixing for any equilibrium state.
$\rho $
) and thus mixing for any equilibrium state.
5.2 Arbitrary
 ${\mathsf {G}},$
coarse geometry viewpoint
${\mathsf {G}},$
coarse geometry viewpoint
Let
![]() ${\mathsf {G}}$
be as in §4. We use freely the notation introduced there and fix from now on a subset
${\mathsf {G}}$
be as in §4. We use freely the notation introduced there and fix from now on a subset
![]() $\vartheta \subset {{{\Delta }}}$
of simple roots.
$\vartheta \subset {{{\Delta }}}$
of simple roots.
Let
![]() be a finitely generated group and denote, for
be a finitely generated group and denote, for
![]() by
by
![]() $|\gamma |$
the word length with respect to a fixed finite symmetric generating set of
$|\gamma |$
the word length with respect to a fixed finite symmetric generating set of
![]()
Definition 5.2.1. A representation
![]() is
is
![]() $\vartheta $
-Anosov if there exist
$\vartheta $
-Anosov if there exist
![]() $c,\mu $
positive such that for all
$c,\mu $
positive such that for all
![]() and
and
![]() $\sigma \in \vartheta $
, one has
$\sigma \in \vartheta $
, one has
The constants c and
![]() $\mu $
will be referred to as the domination constants of
$\mu $
will be referred to as the domination constants of
![]() $\rho .$
$\rho .$
Theorem 5.2.2 follows from the main result by Kapovich, Leeb, and Porti [Reference Kapovich, Leeb and Porti40] and the standard facts from representation theory stated in §4.5, a proof was also reported by Bochi, Potrie, and Sambarino [Reference Bochi, Potrie and Sambarino10].
Theorem 5.2.2. If
![]() is
is
![]() $\vartheta $
-Anosov, then
$\vartheta $
-Anosov, then
![]() is word-hyperbolic. If moreover
is word-hyperbolic. If moreover
![]() $\mathbb {K}=\mathbb {R}$
, then for every
$\mathbb {K}=\mathbb {R}$
, then for every
![]() $\sigma \in \vartheta $
, the representation
$\sigma \in \vartheta $
, the representation
![]() is projective-Anosov (as in §5.1).
is projective-Anosov (as in §5.1).
The following lemma is essentially a consequence of [Reference Bochi, Potrie and Sambarino10, Lemma 4.9]. See [Reference Pozzetti, Sambarino and Wienhard59, Proposition 3.5] for details concerning the non-Archimedean case. The last assertion is classical.
Proposition 5.2.3. (Bochi, Potrie, and Sambarino [Reference Bochi, Potrie and Sambarino10, Proposition 4.9])
If
![]() is
is
![]() $\vartheta $
-Anosov, then for any geodesic ray
$\vartheta $
-Anosov, then for any geodesic ray
![]() $\{\alpha _n\}_0^\infty $
with endpoint x, the limits
$\{\alpha _n\}_0^\infty $
with endpoint x, the limits
exist and do not depend on the ray; they define continuous
![]() $\rho $
-equivariant transverse maps
$\rho $
-equivariant transverse maps
![]() ,
,
![]() . If
. If
![]() is hyperbolic, then
is hyperbolic, then
![]() $\gamma _\rho $
is
$\gamma _\rho $
is
![]() $\vartheta $
-proximal with attracting point
$\vartheta $
-proximal with attracting point
![]() $\xi ^\vartheta (\gamma ^+)=(\gamma _\rho )_\vartheta ^+.$
$\xi ^\vartheta (\gamma ^+)=(\gamma _\rho )_\vartheta ^+.$
Proposition 5.2.3 readily implies the following lemma (recall Remark 4.7.1).
Lemma 5.2.4. Let
![]() be
be
![]() $\vartheta $
-Anosov,
$\vartheta $
-Anosov,
![]() a divergent sequence, and
a divergent sequence, and
![]() Then, as
Then, as
![]() $n\to \infty ,$
one has
$n\to \infty ,$
one has
 $$ \begin{align*}\gamma_n\to x&\Leftrightarrow U_\vartheta(\rho(\gamma_n))\to\xi^\vartheta(x)\\&\Leftrightarrow\text{ there exists }\sigma\in\vartheta\textrm{ such that }\varpi_\sigma\mathscr G_\vartheta(U_{\operatorname{\mathrm{i}}\vartheta}(\rho(\gamma_n)),\xi^\vartheta(x))\to-\infty.\end{align*} $$
$$ \begin{align*}\gamma_n\to x&\Leftrightarrow U_\vartheta(\rho(\gamma_n))\to\xi^\vartheta(x)\\&\Leftrightarrow\text{ there exists }\sigma\in\vartheta\textrm{ such that }\varpi_\sigma\mathscr G_\vartheta(U_{\operatorname{\mathrm{i}}\vartheta}(\rho(\gamma_n)),\xi^\vartheta(x))\to-\infty.\end{align*} $$
We finally record the following useful lemma.
Lemma 5.2.5. (Pozzetti, Sambarino, and Wienhard [Reference Pozzetti, Sambarino and Wienhard59, Lemma 3.6])
Let
be
![]() $\vartheta $
-Anosov, then for every
$\vartheta $
-Anosov, then for every
![]() $\varepsilon>0$
, there exists L such that
$\varepsilon>0$
, there exists L such that

where
![]() $\mathcal N_\varepsilon $
denotes the
$\mathcal N_\varepsilon $
denotes the
![]() $\varepsilon $
-tubular-neighborhood.
$\varepsilon $
-tubular-neighborhood.
Remark 5.2.6. Non-Archimedean case
The existence of continuous
![]() $\rho $
-equivariant maps implies, when
$\rho $
-equivariant maps implies, when
![]() $\mathbb {K}$
is non-Archimedean, that the boundary of
$\mathbb {K}$
is non-Archimedean, that the boundary of
![]() is necessarily a Cantor set and thus
is necessarily a Cantor set and thus
![]() is virtually free. The Gromov–Mineyev of
is virtually free. The Gromov–Mineyev of
![]() is thus a suspension of a sub-shift of finite type and is, hence, metric-Anosov.
is thus a suspension of a sub-shift of finite type and is, hence, metric-Anosov.
5.3 The refraction cocycle verifies Assumption C
By the equivariant boundary maps of
![]() $\rho $
, one can pullback the Buseman–Iwasawa cocycle of
$\rho $
, one can pullback the Buseman–Iwasawa cocycle of
![]() ${\mathsf {G}}$
to obtain a Hölder-cocycle on the boundary of
${\mathsf {G}}$
to obtain a Hölder-cocycle on the boundary of
![]() .
.
Definition 5.3.1. The refraction cocycle of
![]() $\rho $
is
$\rho $
is
,
The limit cone of
![]() $\unicode{x3b2} _{}$
will be denoted by
$\unicode{x3b2} _{}$
will be denoted by
![]() $\mathscr L_{\vartheta ,\rho }$
and referred to as the
$\mathscr L_{\vartheta ,\rho }$
and referred to as the
![]() $\vartheta $
-limit cone of
$\vartheta $
-limit cone of
![]() $\rho $
. The period computation below implies it is the smallest closed cone of
$\rho $
. The period computation below implies it is the smallest closed cone of
![]() ${\mathsf {E}}_\vartheta $
that contains the projections
${\mathsf {E}}_\vartheta $
that contains the projections
![]() We prove moreover that
We prove moreover that
![]() $\unicode{x3b2} _{}$
verifies Assumption C from §3.4.
$\unicode{x3b2} _{}$
verifies Assumption C from §3.4.
Lemma 5.3.2. The periods of
![]() $\unicode{x3b2} _{}$
are
$\unicode{x3b2} _{}$
are
![]() $\unicode{x3b2} _{}(\gamma ,\gamma _+)=\unicode{x3bb} _\vartheta (\gamma _\rho )$
, consequently Assumption
C
holds for
$\unicode{x3b2} _{}(\gamma ,\gamma _+)=\unicode{x3bb} _\vartheta (\gamma _\rho )$
, consequently Assumption
C
holds for
![]() $\unicode{x3b2} _{}$
, in particular,
$\unicode{x3b2} _{}$
, in particular,
![]() $\operatorname {\mathrm {int}}(\mathscr L_{\vartheta ,\rho })^*=\{\varphi \in (\mathscr L_{\vartheta ,\rho })^*:\mathscr h_\varphi <\infty \}$
.
$\operatorname {\mathrm {int}}(\mathscr L_{\vartheta ,\rho })^*=\{\varphi \in (\mathscr L_{\vartheta ,\rho })^*:\mathscr h_\varphi <\infty \}$
.
Proof. The first assertion follows from Proposition 5.2.3. To prove Assumption C holds, one considers any
![]() $\sigma \in \vartheta $
and the representation
$\sigma \in \vartheta $
and the representation
![]() $\unicode{x3c6} _\sigma .$
By Theorem 5.2.2, the composition
$\unicode{x3c6} _\sigma .$
By Theorem 5.2.2, the composition
![]() is projective-Anosov and thus, by equation (19) and Lemma 5.1.2, the form
is projective-Anosov and thus, by equation (19) and Lemma 5.1.2, the form
![]() $\varpi _\sigma \in ({\mathsf {E}}_\vartheta )^*$
has finite entropy. The last assertion follows from Lemma 3.4.2.
$\varpi _\sigma \in ({\mathsf {E}}_\vartheta )^*$
has finite entropy. The last assertion follows from Lemma 3.4.2.
Lemma 3.4.2 and Theorem 3.2.2 give then the following corollary.
Corollary 5.3.3. There exists a Hölder-continuous function
![]() such that for every hyperbolic
such that for every hyperbolic
![]() , one has
, one has
![]() $\int _{[\gamma ]}\mathcal J_{\vartheta ,\rho }=\unicode{x3bb} _\vartheta (\gamma _\rho ).$
For every
$\int _{[\gamma ]}\mathcal J_{\vartheta ,\rho }=\unicode{x3bb} _\vartheta (\gamma _\rho ).$
For every
![]() $\varphi \in \operatorname {\mathrm {int}}(\mathscr L_{\vartheta ,\rho })^*$
, the
$\varphi \in \operatorname {\mathrm {int}}(\mathscr L_{\vartheta ,\rho })^*$
, the
![]() -action on
-action on
![]() defined by
defined by
is properly discontinuous and co-compact. The
![]() $\mathbb {R}$
-translation flow induces on the quotient a flow
$\mathbb {R}$
-translation flow induces on the quotient a flow
![]() $\phi ^\varphi =(\phi ^\varphi _t:{\unicode{x3c7} ^{\varphi }}\to {\unicode{x3c7} ^{\varphi }})_{t\in \mathbb {R}}$
(bi)-Hölder-conjugated to the reparameterization of
$\phi ^\varphi =(\phi ^\varphi _t:{\unicode{x3c7} ^{\varphi }}\to {\unicode{x3c7} ^{\varphi }})_{t\in \mathbb {R}}$
(bi)-Hölder-conjugated to the reparameterization of
![]() ${\mathsf {g}}$
by
${\mathsf {g}}$
by
![]() $\varphi \circ \mathcal J_{\vartheta ,\rho }.$
$\varphi \circ \mathcal J_{\vartheta ,\rho }.$
Definition 5.3.4. The function
![]() $\mathcal J_{\vartheta ,\rho }$
will be referred to as the Ledrappier potential of
$\mathcal J_{\vartheta ,\rho }$
will be referred to as the Ledrappier potential of
![]() $\rho .$
The flow
$\rho .$
The flow
![]() $\phi ^\varphi $
will be called the
$\phi ^\varphi $
will be called the
![]() $\varphi $
-refraction flow of
$\varphi $
-refraction flow of
![]() $\rho $
.
$\rho $
.
5.4 The
 $\vartheta $
-limit cone
$\vartheta $
-limit cone
We mimic some celebrated results by Benoist [Reference Benoist7] for Zariski-dense subgroups and
![]() $\vartheta ={{{\Delta }}}.$
$\vartheta ={{{\Delta }}}.$
Lemma 5.4.1. (Benoist [Reference Benoist6, Proposition 5.1])
For every compact set
![]() $L\subset {\mathsf {G}}$
, there exists a compact set
$L\subset {\mathsf {G}}$
, there exists a compact set
![]() $H\subset {\mathsf {E}}$
such that for every
$H\subset {\mathsf {E}}$
such that for every
![]() $g\in {\mathsf {G}}$
, one has
$g\in {\mathsf {G}}$
, one has
![]() $a(LgL)\subset a(g)+H.$
$a(LgL)\subset a(g)+H.$
Let us also denote
![]() $a_\vartheta =p_\vartheta \circ a.$
$a_\vartheta =p_\vartheta \circ a.$
Proposition 5.4.2. Let
![]() be a
be a
![]() $\vartheta $
-Anosov representation. Then there exists a compact set
$\vartheta $
-Anosov representation. Then there exists a compact set
![]() $D\subset {\mathsf {E}}_\vartheta $
such that
$D\subset {\mathsf {E}}_\vartheta $
such that
![]()
Proof. As
is finitely generated and word-hyperbolic, there exist
![]() $\kappa>0$
and two elements
$\kappa>0$
and two elements
such that for every non-torsion
, there exists
![]() $f\in \{u,v\}$
such that
$f\in \{u,v\}$
such that
![]() $f\gamma $
verifies
$f\gamma $
verifies
As
![]() $\rho $
is
$\rho $
is
![]() $\vartheta $
-Anosov, the above equation implies the element
$\vartheta $
-Anosov, the above equation implies the element
![]() $\rho (f\gamma )$
is
$\rho (f\gamma )$
is
![]() $(r,\varepsilon )$
-proximal on
$(r,\varepsilon )$
-proximal on
![]() $\vartheta $
for some r only depending on
$\vartheta $
for some r only depending on
![]() $\kappa .$
By Proposition 4.8.1, one has
$\kappa .$
By Proposition 4.8.1, one has
for some K only depending on
![]() $\kappa $
and
$\kappa $
and
![]() $\rho .$
We consider the compact set H from the lemma above applied to
$\rho .$
We consider the compact set H from the lemma above applied to
![]() $L=\rho (\{u^{-1},v^{-1}\})$
and we let
$L=\rho (\{u^{-1},v^{-1}\})$
and we let
![]() $D:=p_\vartheta (H)+B(0,K).$
$D:=p_\vartheta (H)+B(0,K).$
We will mainly use the following direct consequence.
Corollary 5.4.3. If
![]() $\varphi \in \operatorname {\mathrm {int}}(\mathscr L_{\vartheta ,\rho })^*$
, then the exponential rate
$\varphi \in \operatorname {\mathrm {int}}(\mathscr L_{\vartheta ,\rho })^*$
, then the exponential rate
Proof. If
![]() $\sigma \in \vartheta $
then, since both intersections
$\sigma \in \vartheta $
then, since both intersections
![]() $\ker \varpi _\sigma \cap \mathscr L_{\vartheta ,\rho }$
and
$\ker \varpi _\sigma \cap \mathscr L_{\vartheta ,\rho }$
and
![]() $\ker \varphi \cap \mathscr L_{\vartheta ,\rho }$
vanish (the first one always does, the second one by the assumption on
$\ker \varphi \cap \mathscr L_{\vartheta ,\rho }$
vanish (the first one always does, the second one by the assumption on
![]() $\varphi $
), the function
$\varphi $
), the function
![]() $\varphi /\varpi _\sigma $
is bounded below away from zero on
$\varphi /\varpi _\sigma $
is bounded below away from zero on
![]() $\mathscr L_{\vartheta ,\rho }.$
By Proposition 5.4.2, there exist positive c and C such that for all hyperbolic
$\mathscr L_{\vartheta ,\rho }.$
By Proposition 5.4.2, there exist positive c and C such that for all hyperbolic
![]() , one has
, one has
Lemma 4.10.1 gives then the desired result.
5.5 Patterson–Sullivan theory along the Anosov roots: existence
In this section, we will construct, for each
![]() $\varphi \in \operatorname {\mathrm {int}}(\mathscr L_{\vartheta ,\rho })^*$
, a
$\varphi \in \operatorname {\mathrm {int}}(\mathscr L_{\vartheta ,\rho })^*$
, a
![]() $\unicode{x3b2} _{\varphi }$
-Patterson–Sullivan measure. (The
$\unicode{x3b2} _{\varphi }$
-Patterson–Sullivan measure. (The
![]() $\vartheta $
-Anosov property is not really used until the uniqueness corollary. The existence presented here works for any discrete group whose limit cone on
$\vartheta $
-Anosov property is not really used until the uniqueness corollary. The existence presented here works for any discrete group whose limit cone on
![]() ${\mathsf {E}}$
does not intersect any wall associated to
${\mathsf {E}}$
does not intersect any wall associated to
![]() $\vartheta $
and replacing
$\vartheta $
and replacing
![]() by
by
The procedure is standard and follows the original idea by Patterson.
We begin by considering the Dirichlet series

It is convergent for every
![]() $s>\delta ^\varphi $
and divergent for every
$s>\delta ^\varphi $
and divergent for every
![]() $s<\delta ^\varphi .$
As it is customary when constructing Patterson–Sullivan measures, we can assume throughout this subsection that
$s<\delta ^\varphi .$
As it is customary when constructing Patterson–Sullivan measures, we can assume throughout this subsection that
![]() $\mathcal P^\varphi (\delta ^\varphi )=\infty ,$
otherwise, one would consider the series
$\mathcal P^\varphi (\delta ^\varphi )=\infty ,$
otherwise, one would consider the series

for some real function h defined, for example, as by Quint [Reference Quint62, Lemma 8.5].
For
![]() $s>\delta ^\varphi $
, consider the probability measure on
$s>\delta ^\varphi $
, consider the probability measure on
![]() $\mathcal F_\vartheta $
defined by
$\mathcal F_\vartheta $
defined by

Lemma 5.5.1. For every
, the signed measure

weakly converges to
![]() $0$
as
$0$
as
![]() $s\searrow \delta ^\varphi .$
$s\searrow \delta ^\varphi .$
This is a standard argument that can be found, for example, in [Reference Pozzetti, Sambarino and Wienhard59, Lemma 5.11].
Proof. It is sufficient to check the convergence for continuous functions. If
![]() $f:\mathcal F_\vartheta \to \mathbb {R}$
is continuous, then
$f:\mathcal F_\vartheta \to \mathbb {R}$
is continuous, then

By Lemma 4.9.2 and uniform continuity of f, the convergence follows.
Lemma 5.5.2. Let
![]() $\nu ^\varphi $
be any weak-star limit of
$\nu ^\varphi $
be any weak-star limit of
![]() $\nu _s$
when
$\nu _s$
when
![]() $s\searrow \delta ^\varphi .$
Then, the support of
$s\searrow \delta ^\varphi .$
Then, the support of
![]() $\nu ^\varphi $
is contained in
$\nu ^\varphi $
is contained in
![]() Moreover, for every
Moreover, for every
![]() , one has
, one has
Proof. The first statement follows at once from Lemma 5.2.5 since we assumed
![]() $\mathcal P^\varphi (\delta ^\varphi )=\infty .$
For the second statement, consider a sequence
$\mathcal P^\varphi (\delta ^\varphi )=\infty .$
For the second statement, consider a sequence
![]() $s_k\searrow \delta ^\varphi $
such that
$s_k\searrow \delta ^\varphi $
such that
![]() $\nu _{s_k}\to \nu ^\varphi .$
One then has
$\nu _{s_k}\to \nu ^\varphi .$
One then has

where by Quint’s Lemma 4.9.3 and the fact that
![]() $\varphi \circ p_\vartheta =\varphi ,$
one has
$\varphi \circ p_\vartheta =\varphi ,$
one has
![]() $\varepsilon '(\eta ,\gamma )\to 0$
as
$\varepsilon '(\eta ,\gamma )\to 0$
as
![]() $\min _{\sigma \in \vartheta }\sigma (a(\gamma _\rho ))\to \infty .$
Taking the limit as
$\min _{\sigma \in \vartheta }\sigma (a(\gamma _\rho ))\to \infty .$
Taking the limit as
![]() $s_k\searrow \delta ^\varphi $
, one has, since we assumed
$s_k\searrow \delta ^\varphi $
, one has, since we assumed
![]() $\mathcal P^\varphi (\delta ^\varphi )=\infty ,$
that only elements
$\mathcal P^\varphi (\delta ^\varphi )=\infty ,$
that only elements
with arbitrary big
![]() $|\gamma |$
count in the sum. Since
$|\gamma |$
count in the sum. Since
![]() $\rho $
is
$\rho $
is
![]() $\vartheta $
-Anosov, this is equivalent to considering elements
$\vartheta $
-Anosov, this is equivalent to considering elements
such that
is arbitrarily big. The result then follows as
![]() $\varepsilon (\eta ,s_k)\to 0$
by Lemma 5.5.2 and
$\varepsilon (\eta ,s_k)\to 0$
by Lemma 5.5.2 and
![]() $\varepsilon '(\eta ,\gamma )$
is arbitrarily small.
$\varepsilon '(\eta ,\gamma )$
is arbitrarily small.
Since Assumption C holds for
![]() $\unicode{x3b2} _{}$
(Lemma 5.3.2), §3.3 is applied to give the following corollary.
$\unicode{x3b2} _{}$
(Lemma 5.3.2), §3.3 is applied to give the following corollary.
Corollary 5.5.3. For every
![]() $\varphi \in \operatorname {\mathrm {int}}(\mathscr L_{\vartheta ,\rho })^*$
, there exists a
$\varphi \in \operatorname {\mathrm {int}}(\mathscr L_{\vartheta ,\rho })^*$
, there exists a
![]() $\unicode{x3b2} _{\varphi }$
-Patterson–Sullivan measure
$\unicode{x3b2} _{\varphi }$
-Patterson–Sullivan measure
![]() $\mu ^\varphi :=(\xi ^\vartheta )_*\nu ^\varphi $
of exponent
$\mu ^\varphi :=(\xi ^\vartheta )_*\nu ^\varphi $
of exponent
![]() $\delta ^\varphi .$
Such a measure is ergodic and, moreover, one has
$\delta ^\varphi .$
Such a measure is ergodic and, moreover, one has
![]() $\delta ^\varphi =\mathscr h_\varphi .$
If
$\delta ^\varphi =\mathscr h_\varphi .$
If
![]() $\psi \in \operatorname {\mathrm {int}}(\mathscr L_{\vartheta ,\rho })^*$
is such that
$\psi \in \operatorname {\mathrm {int}}(\mathscr L_{\vartheta ,\rho })^*$
is such that
![]() $\mu ^\psi \ll \mu ^\varphi $
, then for every hyperbolic
$\mu ^\psi \ll \mu ^\varphi $
, then for every hyperbolic
, one has
and, in particular,
![]() $\mu ^\psi =\mu ^\varphi .$
$\mu ^\psi =\mu ^\varphi .$
The above corollary was previously established by Dey and Kapovich [Reference Dey and Kapovich29, Main Theorem] for real algebraic groups,
![]() $\operatorname {\mathrm {i}}$
-invariant functionals
$\operatorname {\mathrm {i}}$
-invariant functionals
![]() $\varphi \in \operatorname {\mathrm {int}}({\mathfrak a}^+)^*$
, and
$\varphi \in \operatorname {\mathrm {int}}({\mathfrak a}^+)^*$
, and
![]() $\operatorname {\mathrm {i}}$
-invariant subsets
$\operatorname {\mathrm {i}}$
-invariant subsets
![]() $\vartheta .$
The equality
$\vartheta .$
The equality
![]() $\delta ^\varphi =\mathscr h_\varphi $
, together with more information, can also be found in Glorieux, Monclair, and Tholozan’s work [Reference Glorieux, Monclair and Tholozan32, Theorem 2.31(2)] for real groups.
$\delta ^\varphi =\mathscr h_\varphi $
, together with more information, can also be found in Glorieux, Monclair, and Tholozan’s work [Reference Glorieux, Monclair and Tholozan32, Theorem 2.31(2)] for real groups.
Remark 5.5.4. We conclude by remarking that for
![]() $\varphi \in \operatorname {\mathrm {int}}(\mathscr L_{\vartheta ,\rho })^*,$
the existence assumptions of §3.3 are guaranteed for
$\varphi \in \operatorname {\mathrm {int}}(\mathscr L_{\vartheta ,\rho })^*,$
the existence assumptions of §3.3 are guaranteed for
![]() $\unicode{x3b2} _{\varphi }.$
Indeed, Proposition 5.5.3 states the existence of a Patterson–Sullivan measure
$\unicode{x3b2} _{\varphi }.$
Indeed, Proposition 5.5.3 states the existence of a Patterson–Sullivan measure
![]() $\mu ^\varphi $
for
$\mu ^\varphi $
for
![]() $\unicode{x3b2} _{\varphi }.$
The cocycle
$\unicode{x3b2} _{\varphi }.$
The cocycle
is dual to
![]() $\unicode{x3b2} _{}$
and moreover, from equation (22), the function
$\unicode{x3b2} _{}$
and moreover, from equation (22), the function
![]()
is a Gromov product for the pair
![]() $(\bar {\unicode{x3b2} }_{\varphi },\unicode{x3b2} _{\varphi }).$
Finally, exchanging
$(\bar {\unicode{x3b2} }_{\varphi },\unicode{x3b2} _{\varphi }).$
Finally, exchanging
![]() $\vartheta $
with
$\vartheta $
with
![]() $\operatorname {\mathrm {i}}\vartheta ,$
Proposition 5.5.3 provides a Patterson–Sullivan measure for
$\operatorname {\mathrm {i}}\vartheta ,$
Proposition 5.5.3 provides a Patterson–Sullivan measure for
![]() $\bar {\unicode{x3b2} }_{\varphi }.$
We can thus apply the results from §§3.4 and 3.5.
$\bar {\unicode{x3b2} }_{\varphi }.$
We can thus apply the results from §§3.4 and 3.5.
5.6 Cartan’s basins have controlled overlaps
The job of understanding the overlaps of Cartan’s basins for Anosov representations has been carried out by Pozzetti, Sambarino, and Wienhard [Reference Pozzetti, Sambarino and Wienhard58]. The idea is to compare the Cartan’s basins of elements
![]() $\gamma _\rho ,$
for hyperbolic
$\gamma _\rho ,$
for hyperbolic
![]() with the coarse cone type of
with the coarse cone type of
![]() $\gamma .$
$\gamma .$
Let
![]() $c_0,c_1$
be positive and
$c_0,c_1$
be positive and
![]() $I\subset \mathbb {Z}$
an interval. Then, a
$I\subset \mathbb {Z}$
an interval. Then, a
![]() $(c_0,c_1)$
-quasigeodesic is a sequence
$(c_0,c_1)$
-quasigeodesic is a sequence
such that for every pair
![]() $j,l$
in the interval I, one has
$j,l$
in the interval I, one has
The coarse cone type at infinity of
consists of endpoints on
of quasi geodesic rays based at
![]() $\gamma ^{-1}$
passing through the identity (see Figure 1):
$\gamma ^{-1}$
passing through the identity (see Figure 1):


Figure 1 The coarse cone type at infinity, the black broken lines are
![]() $(c_0,c_1)$
-quasi-geodesics.
$(c_0,c_1)$
-quasi-geodesics.
Pozzetti, Sambarino, and Wienhard [Reference Pozzetti, Sambarino and Wienhard58, Proposition 3.3] together with Bochi, Potrie, and Sambarino [Reference Bochi, Potrie and Sambarino10, Lemma 2.5] (see also [Reference Pozzetti, Sambarino and Wienhard59, Proposition 3.3]) give the following. The last statement can be found in [Reference Pozzetti, Sambarino and Wienhard58, Proposition 3.5].
Proposition 5.6.1. (Pozzetti, Sambarino, and Wienhard [Reference Pozzetti, Sambarino and Wienhard58, Proposition 3.3])
For a given
![]() $\alpha>0$
, there exist
$\alpha>0$
, there exist
![]() $c_0,c_1,$
depending on
$c_0,c_1,$
depending on
![]() $\alpha $
and the domination constants of
$\alpha $
and the domination constants of
![]() $\rho ,$
such that for every hyperbolic
$\rho ,$
such that for every hyperbolic
![]() , one has
, one has
Reciprocally, there exists
![]() $\alpha ';$
only depending on
$\alpha ';$
only depending on
![]() $c_0,c_1$
and the domination constants of
$c_0,c_1$
and the domination constants of
![]() $\rho ,$
such that
$\rho ,$
such that
There exists then
![]() $N\in \mathbb {N},$
only depending on
$N\in \mathbb {N},$
only depending on
![]() $c_0,c_1$
and the domination constants of
$c_0,c_1$
and the domination constants of
![]() $\rho $
such that, for all
$\rho $
such that, for all
![]() $t\in \mathbb {N}$
, the family
$t\in \mathbb {N}$
, the family
is an open covering of
![]() and such that every element
and such that every element
![]() $\xi ^\vartheta (x)$
belongs to at most N elements of the covering
$\xi ^\vartheta (x)$
belongs to at most N elements of the covering
![]() $\mathcal U_t.$
$\mathcal U_t.$
5.7 Sullivan’s shadow lemma
We establish now a version of Sullivan’s shadow lemma.
Lemma 5.7.1. Consider
![]() $\varphi \in ({\mathsf {E}}_\vartheta )^* $
and let
$\varphi \in ({\mathsf {E}}_\vartheta )^* $
and let
![]() $\mu $
be a
$\mu $
be a
![]() $\unicode{x3b2} _{\varphi }$
-Patterson–Sullivan measure of exponent
$\unicode{x3b2} _{\varphi }$
-Patterson–Sullivan measure of exponent
![]() $\delta .$
Let
$\delta .$
Let
![]() $\nu =\xi ^{\vartheta }_*\mu .$
Then given
$\nu =\xi ^{\vartheta }_*\mu .$
Then given
![]() $\alpha>0$
, there exist constants
$\alpha>0$
, there exist constants
![]() $C, C'$
, and
$C, C'$
, and
![]() $L\in \mathbb {N}$
such that for every
$L\in \mathbb {N}$
such that for every
![]() with
with
![]() $|\gamma |\geq L$
, one has
$|\gamma |\geq L$
, one has
Proof. It suffices to establish that there exist
![]() $\alpha $
and
$\alpha $
and
![]() $\kappa>0$
such that for all large enough
$\kappa>0$
such that for all large enough
![]() , one has
, one has
![]() $\nu (B_{\vartheta ,\alpha }(\gamma _\rho ))\geq \kappa .$
Indeed, using this fact, the lemma follows from the defining equations (27) and (23).
$\nu (B_{\vartheta ,\alpha }(\gamma _\rho ))\geq \kappa .$
Indeed, using this fact, the lemma follows from the defining equations (27) and (23).
To establish the desired lower bound, we suppose by contradiction that there exists
![]() $\alpha _n\to \infty , \gamma _n\to \infty $
such that
$\alpha _n\to \infty , \gamma _n\to \infty $
such that
![]() $\nu (B_{\vartheta ,\alpha _n}((\gamma _n)_\rho ))\to 0$
as
$\nu (B_{\vartheta ,\alpha _n}((\gamma _n)_\rho ))\to 0$
as
![]() $n\to \infty .$
We can then extract a subsequence
$n\to \infty .$
We can then extract a subsequence
![]() $(\gamma _{n_k})$
such that
$(\gamma _{n_k})$
such that
Moreover, since
![]() $\rho $
is
$\rho $
is
![]() $\vartheta $
-Anosov, Lemma 5.2.5 guarantees that
$\vartheta $
-Anosov, Lemma 5.2.5 guarantees that
![]() $Y=\xi ^{\operatorname {\mathrm {i}}\vartheta }(y)$
for some
$Y=\xi ^{\operatorname {\mathrm {i}}\vartheta }(y)$
for some
![]() Also, since
Also, since
![]() $\nu (B_{\vartheta ,\alpha _{n_k}}((\gamma _{n_k})_\rho ))\to 0$
and
$\nu (B_{\vartheta ,\alpha _{n_k}}((\gamma _{n_k})_\rho ))\to 0$
and
![]() $\alpha _{n_k}\to \infty $
, we get that the complement
$\alpha _{n_k}\to \infty $
, we get that the complement
 $$ \begin{align*} &(B_{\vartheta,\alpha_{n_k}}((\gamma_{n_k})_\rho))^c\\ & \quad =\{X\in\mathcal F_\vartheta:\text{ there exists }\sigma\in\vartheta\ \textrm{such that}\ \varpi_\sigma\mathscr G_\vartheta(U_{\operatorname{\mathrm{i}}\vartheta}((\gamma_{n_k}^{-1})_\rho),X)\leq-\alpha_n\}\end{align*} $$
$$ \begin{align*} &(B_{\vartheta,\alpha_{n_k}}((\gamma_{n_k})_\rho))^c\\ & \quad =\{X\in\mathcal F_\vartheta:\text{ there exists }\sigma\in\vartheta\ \textrm{such that}\ \varpi_\sigma\mathscr G_\vartheta(U_{\operatorname{\mathrm{i}}\vartheta}((\gamma_{n_k}^{-1})_\rho),X)\leq-\alpha_n\}\end{align*} $$
converges to the subset of
![]() $\mathcal F_\vartheta $
$\mathcal F_\vartheta $
and that this subset has total
![]() $\nu $
-mass. Since the support of
$\nu $
-mass. Since the support of
![]() $\nu $
is contained in
$\nu $
is contained in
![]() and the equivariant maps are transverse (Proposition 5.2.3), one has that
and the equivariant maps are transverse (Proposition 5.2.3), one has that
has total
![]() $\nu $
-mass. However, considering
$\nu $
-mass. However, considering
![]() with
with
![]() $\gamma y\neq y$
, we get, since
$\gamma y\neq y$
, we get, since
that
![]() $\nu \{\xi ^1(\gamma y)\}>0,$
contradicting that
$\nu \{\xi ^1(\gamma y)\}>0,$
contradicting that
![]() $\{\xi ^\vartheta (y)\}$
has total
$\{\xi ^\vartheta (y)\}$
has total
![]() $\nu $
-mass.
$\nu $
-mass.
Corollary 5.7.2. For every
![]() $\varphi \in \operatorname {\mathrm {int}}(\mathscr L_{\vartheta ,\rho })^*$
, one has
$\varphi \in \operatorname {\mathrm {int}}(\mathscr L_{\vartheta ,\rho })^*$
, one has

5.8 Patterson–Sullivan theory along the Anosov roots: surjectivity
We prove here surjectivity of the map
![]() $\varphi \mapsto \mu ^\varphi $
defined in §5.5.
$\varphi \mapsto \mu ^\varphi $
defined in §5.5.
The following proposition should be compared with [Reference Pozzetti, Sambarino and Wienhard58, Theorem 5.14], where a similar result is obtained for measures on the flag space
![]() $\mathcal F_\theta ,$
for
$\mathcal F_\theta ,$
for
![]() $\theta $
not necessarily equal to
$\theta $
not necessarily equal to
![]() $\vartheta $
but assuming that
$\vartheta $
but assuming that
![]() $\vartheta \cap \theta \neq \emptyset .$
$\vartheta \cap \theta \neq \emptyset .$
Proposition 5.8.1. Consider
![]() $\varphi \in ({\mathsf {E}}_\vartheta )^*.$
If there exists a
$\varphi \in ({\mathsf {E}}_\vartheta )^*.$
If there exists a
![]() $\unicode{x3b2} _{\varphi }$
-Patterson–Sullivan measure
$\unicode{x3b2} _{\varphi }$
-Patterson–Sullivan measure
![]() $\mu $
of exponent
$\mu $
of exponent
![]() $\delta $
, then
$\delta $
, then
![]() $\varphi \in \operatorname {\mathrm {int}}(\mathscr L_{\vartheta ,\rho })^*, \delta = \delta ^\varphi $
, and
$\varphi \in \operatorname {\mathrm {int}}(\mathscr L_{\vartheta ,\rho })^*, \delta = \delta ^\varphi $
, and
![]() $\mu =\mu ^\varphi .$
$\mu =\mu ^\varphi .$
Proof. We let
![]() $\nu =\xi ^\vartheta _*\mu .$
Using Proposition 5.6.1, we get a family of coverings
$\nu =\xi ^\vartheta _*\mu .$
Using Proposition 5.6.1, we get a family of coverings
![]() $\mathcal U_t$
with bounded overlap. In combination with Lemma 5.7.1, one has for t large enough that
$\mathcal U_t$
with bounded overlap. In combination with Lemma 5.7.1, one has for t large enough that

for some constant
![]() $K>0.$
This is to say, there exists
$K>0.$
This is to say, there exists
![]() $\kappa>0$
such that for all
$\kappa>0$
such that for all
![]() $t\in \mathbb {R}_+$
large, one has
$t\in \mathbb {R}_+$
large, one has
![]() $\sum _{\gamma :t\leq |\gamma |\leq t+1}e^{-\delta \varphi (a(\gamma _\rho ))}\leq \kappa ,$
which gives in turn that
$\sum _{\gamma :t\leq |\gamma |\leq t+1}e^{-\delta \varphi (a(\gamma _\rho ))}\leq \kappa ,$
which gives in turn that
 $$ \begin{align*}\sum_{\gamma:|\gamma|\leq t}e^{-\delta\varphi(a(\gamma_\rho))}\leq\kappa t.\end{align*} $$
$$ \begin{align*}\sum_{\gamma:|\gamma|\leq t}e^{-\delta\varphi(a(\gamma_\rho))}\leq\kappa t.\end{align*} $$
A standard argument (using for example §4.8) permits to replace Cartan projections with Jordan projections giving
 $$ \begin{align*}\sum_{[\gamma]:p([\gamma])\leq t}e^{-\delta\varphi(\unicode{x3bb}(\gamma_\rho))}=\sum_{[\gamma]:p([\gamma])\leq t}e^{-\ell_{\delta\mathcal J_{\vartheta,\rho}^\varphi}(\gamma)}\leq\kappa' t,\end{align*} $$
$$ \begin{align*}\sum_{[\gamma]:p([\gamma])\leq t}e^{-\delta\varphi(\unicode{x3bb}(\gamma_\rho))}=\sum_{[\gamma]:p([\gamma])\leq t}e^{-\ell_{\delta\mathcal J_{\vartheta,\rho}^\varphi}(\gamma)}\leq\kappa' t,\end{align*} $$
for a suitable
![]() $\kappa ',$
where
$\kappa ',$
where
![]() $p([\gamma ])$
is the
$p([\gamma ])$
is the
![]() ${\mathsf {g}}$
-period of the periodic orbit associated to
${\mathsf {g}}$
-period of the periodic orbit associated to
![]() $[\gamma ],$
and
$[\gamma ],$
and
![]() $\mathcal J_{\vartheta ,\rho }^\varphi $
is the Ledrappier potential of
$\mathcal J_{\vartheta ,\rho }^\varphi $
is the Ledrappier potential of
![]() $\unicode{x3b2} _{\varphi }.$
Equation (5) for the pressure function gives then
$\unicode{x3b2} _{\varphi }.$
Equation (5) for the pressure function gives then
Consequently, Lemma 2.2.7 gives that
![]() $\mathcal J_{\vartheta ,\rho }^\varphi $
is Livšic-cohomologous to a positive function, this is to say,
$\mathcal J_{\vartheta ,\rho }^\varphi $
is Livšic-cohomologous to a positive function, this is to say,
![]() $\varphi \in \operatorname {\mathrm {int}}(\mathscr L_{\vartheta ,\rho })^*.$
Finally, since Remark 5.5.4 guarantees the existence assumptions of §3.3 for
$\varphi \in \operatorname {\mathrm {int}}(\mathscr L_{\vartheta ,\rho })^*.$
Finally, since Remark 5.5.4 guarantees the existence assumptions of §3.3 for
![]() $\unicode{x3b2} _{\varphi },$
the remaining two equalities in the statement follow from Corollary 3.3.2.
$\unicode{x3b2} _{\varphi },$
the remaining two equalities in the statement follow from Corollary 3.3.2.
5.9 The critical hypersurface parameterizes Patterson–Sullivan measures
By Lemma 5.3, Assumption C holds for
![]() $\unicode{x3b2} _{}$
and thus §3.4 applies. Define the
$\unicode{x3b2} _{}$
and thus §3.4 applies. Define the
![]() $\vartheta $
-critical hypersurface, respectively
$\vartheta $
-critical hypersurface, respectively
![]() $\vartheta $
-convergence domain, of
$\vartheta $
-convergence domain, of
![]() $\rho $
by
$\rho $
by

Moreover, by Corollary 5.5.3, one has
![]() $\delta ^\varphi =\mathscr h_\varphi $
, so one has the equalities
$\delta ^\varphi =\mathscr h_\varphi $
, so one has the equalities

where the last equality comes from Corollary 5.7.2.
For
![]() $\varphi \in \mathcal Q_{\vartheta ,\rho }$
, we consider the dynamical intersection map
$\varphi \in \mathcal Q_{\vartheta ,\rho }$
, we consider the dynamical intersection map
![]() $\mathbf {I}_\varphi =\mathbf {I}_\varphi ^{\unicode{x3b2} _{}}:({\mathsf {E}}_\vartheta )^*\to \mathbb {R},$
associated to the cocycle
$\mathbf {I}_\varphi =\mathbf {I}_\varphi ^{\unicode{x3b2} _{}}:({\mathsf {E}}_\vartheta )^*\to \mathbb {R},$
associated to the cocycle
![]() $\unicode{x3b2} _{}$
as in §3.4 and defined by
$\unicode{x3b2} _{}$
as in §3.4 and defined by

where
Let
![]() $\mathrm {Ann}(\mathscr L_{\vartheta ,\rho })$
be the annihilator of the
$\mathrm {Ann}(\mathscr L_{\vartheta ,\rho })$
be the annihilator of the
![]() $\vartheta $
-limit cone and denote by
$\vartheta $
-limit cone and denote by
the quotient projection. As before, the map
![]() $\mathbf {I}^{\unicode{x3b2} _{}}$
is also well defined on
$\mathbf {I}^{\unicode{x3b2} _{}}$
is also well defined on
![]() $\pi ^\vartheta _\rho (\mathcal Q_{\vartheta ,\rho })\times ({\mathsf {E}}_\vartheta )^*/\mathrm {Ann}(\mathscr L_{\vartheta ,\rho }).$
$\pi ^\vartheta _\rho (\mathcal Q_{\vartheta ,\rho })\times ({\mathsf {E}}_\vartheta )^*/\mathrm {Ann}(\mathscr L_{\vartheta ,\rho }).$
Some statements in the following corollary were previously established by Sambarino [Reference Sambarino64] for
![]() $\mathbb {K}=\mathbb {R}$
and Zariski-dense
$\mathbb {K}=\mathbb {R}$
and Zariski-dense
![]() $\vartheta $
-Anosov representations of closed negatively curved manifolds.
$\vartheta $
-Anosov representations of closed negatively curved manifolds.
Corollary 5.9.1. The sets
![]() $\mathcal Q_{\vartheta ,\rho }$
and
$\mathcal Q_{\vartheta ,\rho }$
and
![]() $\pi ^\vartheta _\rho (\mathcal Q_{\vartheta ,\rho })$
are closed co-dimension-one analytic sub-manifolds. The latter bounds the strictly convex set
$\pi ^\vartheta _\rho (\mathcal Q_{\vartheta ,\rho })$
are closed co-dimension-one analytic sub-manifolds. The latter bounds the strictly convex set
![]() $\pi ^\vartheta _\rho (\mathcal D_{\vartheta ,\rho }).$
The map
$\pi ^\vartheta _\rho (\mathcal D_{\vartheta ,\rho }).$
The map
is an analytic diffeomorphism between
![]() $\pi ^\vartheta _\rho (\mathcal Q_{\vartheta ,\rho })$
and directions in the relative interior of
$\pi ^\vartheta _\rho (\mathcal Q_{\vartheta ,\rho })$
and directions in the relative interior of
![]() $\mathscr L_{\vartheta ,\rho }.$
$\mathscr L_{\vartheta ,\rho }.$
We now prove the following proposition.
Proposition 5.9.2. The map
![]() $\varphi \mapsto \mu ^\varphi $
is an analytic homeomorphism from the manifold
$\varphi \mapsto \mu ^\varphi $
is an analytic homeomorphism from the manifold
![]() $\pi ^\vartheta _\rho (\mathcal Q_{\vartheta ,\rho })$
to the space of Patterson–Sullivan measures supported on
$\pi ^\vartheta _\rho (\mathcal Q_{\vartheta ,\rho })$
to the space of Patterson–Sullivan measures supported on
![]()
Proof. By uniqueness in Corollary 5.5.3, the map
![]() $\varphi \mapsto \mu ^\varphi $
is well defined and injective. Regularity follows from Remark 3.3.3 and analytic variation of equilibrium states (Theorem 2.3.3). Surjectivity follows from Proposition 5.8.1.
$\varphi \mapsto \mu ^\varphi $
is well defined and injective. Regularity follows from Remark 3.3.3 and analytic variation of equilibrium states (Theorem 2.3.3). Surjectivity follows from Proposition 5.8.1.
Proposition 5.9.2 was previously established by Lee and Oh [Reference Lee and Oh46, Theorem 1.3] for
![]() $\mathbb {K}=\mathbb {R}$
and
$\mathbb {K}=\mathbb {R}$
and
![]() ${{{\Delta }}}$
-Anosov Zariski-dense representations. The convergence domain
${{{\Delta }}}$
-Anosov Zariski-dense representations. The convergence domain
![]() $\mathcal D_{{{{\Delta }}},\rho }$
is dual to Quint’s growth indicator function [Reference Quint61].
$\mathcal D_{{{{\Delta }}},\rho }$
is dual to Quint’s growth indicator function [Reference Quint61].
Remark 5.10. Observe that, by definition, a
![]() $\unicode{x3b2} _{\varphi }$
-Patterson–Sullivan measure has its support on
$\unicode{x3b2} _{\varphi }$
-Patterson–Sullivan measure has its support on
![]() and thus on
and thus on
![]() when pushed to
when pushed to
![]() $\mathcal F_\vartheta .$
One could more generally study measures on
$\mathcal F_\vartheta .$
One could more generally study measures on
![]() $\mathcal F_\vartheta $
verifying
$\mathcal F_\vartheta $
verifying
without imposing conditions on their support. Such measures exist, for example, the
![]() ${\mathsf {K}}$
-invariant measure on
${\mathsf {K}}$
-invariant measure on
![]() $\mathcal F_\vartheta ,$
but their exponent is too large. The question would be totally settled if the following had an affirmative answer: Is the support of a measure verifying equation (28) with
$\mathcal F_\vartheta ,$
but their exponent is too large. The question would be totally settled if the following had an affirmative answer: Is the support of a measure verifying equation (28) with
![]() $\delta =\delta ^\varphi $
necessarily contained on
$\delta =\delta ^\varphi $
necessarily contained on
![]() ?
?
5.11 Variation of the critical hypersurface
We record the following consequence of Bridgeman et al [Reference Bridgeman, Canary, Labourie and Sambarino17, §6.3]
Corollary 5.11.1. (Bridgeman et al [Reference Bridgeman, Canary, Labourie and Sambarino17])
Let
![]() be an analytic family of
be an analytic family of
![]() $\vartheta $
-Anosov representations. Then, Livšic-cohomology class of the Ledrappier potential
$\vartheta $
-Anosov representations. Then, Livšic-cohomology class of the Ledrappier potential
![]() associated varies analytically with
associated varies analytically with
![]() $u.$
$u.$
Consequently, we can apply Corollary 2.6.5 to obtain the following corollary.
Corollary 5.11.2. Let
![]() be an analytic family of
be an analytic family of
![]() $\vartheta $
-Anosov representations. Then the critical hypersurface
$\vartheta $
-Anosov representations. Then the critical hypersurface
![]() $\mathcal Q_{\vartheta ,\rho _u}$
varies analytically (on compact sets of
$\mathcal Q_{\vartheta ,\rho _u}$
varies analytically (on compact sets of
![]() ${\mathsf {E}}_\vartheta $
) with the representation
${\mathsf {E}}_\vartheta $
) with the representation
![]() $u.$
$u.$
5.12 Consequences of the skew-product structure
Consider
![]() $\varphi \in \operatorname {\mathrm {int}}(\mathscr L_{\vartheta ,\rho })^*.$
By Remark 5.5.4, we can freely apply results from §§3.4 and 3.5 to the cocycle
$\varphi \in \operatorname {\mathrm {int}}(\mathscr L_{\vartheta ,\rho })^*.$
By Remark 5.5.4, we can freely apply results from §§3.4 and 3.5 to the cocycle
![]() $\unicode{x3b2} _{\varphi }.$
$\unicode{x3b2} _{\varphi }.$
Let
![]() ${\mathsf {u}}_\varphi ={\mathsf {T}}_{\mathscr h_\varphi \varphi }\mathcal Q_{\vartheta ,\rho }\in \mathbb {P}(\mathscr L_{\vartheta ,\rho })$
be the growth direction of
${\mathsf {u}}_\varphi ={\mathsf {T}}_{\mathscr h_\varphi \varphi }\mathcal Q_{\vartheta ,\rho }\in \mathbb {P}(\mathscr L_{\vartheta ,\rho })$
be the growth direction of
![]() $\varphi $
. By §3.4, the half-line
$\varphi $
. By §3.4, the half-line
![]() ${\mathsf {u}}_\varphi \cap \mathscr L_{\vartheta ,\rho }$
lies in the relative interior of
${\mathsf {u}}_\varphi \cap \mathscr L_{\vartheta ,\rho }$
lies in the relative interior of
![]() $\mathscr L_{\vartheta ,\rho }$
(and every direction in this relative interior is obtained in this fashion).
$\mathscr L_{\vartheta ,\rho }$
(and every direction in this relative interior is obtained in this fashion).
Consider the
![]() $\varphi $
-Bowen–Margulis measure
$\varphi $
-Bowen–Margulis measure
![]() $\Omega ^\varphi $
on
$\Omega ^\varphi $
on
![]() defined as induction on the quotient by
defined as induction on the quotient by
Consider
![]() $u_\varphi \in {\mathsf {u}}_\varphi $
with
$u_\varphi \in {\mathsf {u}}_\varphi $
with
![]() $\varphi (u_\varphi )=1$
and denote by
$\varphi (u_\varphi )=1$
and denote by
![]() the directional flow induced on the quotient of
the directional flow induced on the quotient of
The ergodic dichotomy from §3.6 then gives the following theorem.
Theorem 5.12.1. Assume
![]() $\mathbb {K}=\mathbb {R}$
and
$\mathbb {K}=\mathbb {R}$
and
![]() $\rho $
is Zariski-dense, and let
$\rho $
is Zariski-dense, and let
![]() $\varphi \in \operatorname {\mathrm {int}}(\mathscr L_{\vartheta ,\rho })^*.$
If
$\varphi \in \operatorname {\mathrm {int}}(\mathscr L_{\vartheta ,\rho })^*.$
If
![]() $|\vartheta |\leq 2$
, then the directional flow
$|\vartheta |\leq 2$
, then the directional flow
![]() $\unicode{x3c9} ^\varphi $
is ergodic with respect to
$\unicode{x3c9} ^\varphi $
is ergodic with respect to
![]() $\Omega ^\varphi ,$
in particular,
$\Omega ^\varphi ,$
in particular,
![]() $\mathcal K(\unicode{x3c9} ^\varphi )$
has total mass. If
$\mathcal K(\unicode{x3c9} ^\varphi )$
has total mass. If
![]() $|\vartheta |\geq 4$
, then
$|\vartheta |\geq 4$
, then
![]() $\mathcal K(\unicode{x3c9} ^\varphi )$
has measure
$\mathcal K(\unicode{x3c9} ^\varphi )$
has measure
![]() $0.$
$0.$
5.13 Directional conical points
The present task is to study the set of points on
![]() that are conical in the direction
that are conical in the direction
![]() ${\mathsf {u}}_\varphi .$
${\mathsf {u}}_\varphi .$
Consider
![]() and a sequence
and a sequence
![]() with
with
![]() $\gamma _n\to y.$
Then we say that
$\gamma _n\to y.$
Then we say that
![]() $\gamma _n$
converges conically to y if for every
$\gamma _n$
converges conically to y if for every
![]() , the sequence
, the sequence
![]() $\gamma _n^{-1}(z,y)$
remains on a compact subset of
$\gamma _n^{-1}(z,y)$
remains on a compact subset of
![]()
Remark 5.13.1. Equivalently, since any compact subset of
![]() is contained in a compact subset of the form
is contained in a compact subset of the form
![]() for a fixed
for a fixed
![]() $\kappa ,$
one has that
$\kappa ,$
one has that
![]() $\gamma _n\to y$
conically if and only if there exists a geodesic ray
$\gamma _n\to y$
conically if and only if there exists a geodesic ray
![]() $\{\alpha _i\}_0^\infty $
on
$\{\alpha _i\}_0^\infty $
on
![]() converging to
converging to
![]() $y,$
such that
$y,$
such that
![]() $\{\gamma _n\}$
is at bounded Hausdorff distance from
$\{\gamma _n\}$
is at bounded Hausdorff distance from
![]() $\{\alpha _i\}_0^\infty .$
It follows then the existence of constants,
$\{\alpha _i\}_0^\infty .$
It follows then the existence of constants,
![]() $c_0,c_1$
, such that for all n, one has
$c_0,c_1$
, such that for all n, one has
Let us fix an (auxiliary) Euclidean norm on
![]() ${\mathsf {E}}_\vartheta $
and denote by
${\mathsf {E}}_\vartheta $
and denote by
![]() $B(v,r)$
the associated ball of radius r about
$B(v,r)$
the associated ball of radius r about
![]() $v.$
The tube of size r about
$v.$
The tube of size r about
![]() ${\mathsf {u}}_\varphi $
is the tubular neighborhood:
${\mathsf {u}}_\varphi $
is the tubular neighborhood:
Definition 5.13.2. We say that
![]() is
is
![]() $(r,\varphi )$
-conical if there exists a conical sequence
$(r,\varphi )$
-conical if there exists a conical sequence
![]() converging to y such that for all n,
converging to y such that for all n,
We say that y is
![]() $\varphi $
-conical if it is
$\varphi $
-conical if it is
![]() $(r,\varphi )$
-conical for some
$(r,\varphi )$
-conical for some
![]() $r.$
$r.$
Let us denote by
![]() the set of
the set of
![]() $(r,\varphi )$
-conical points and by
$(r,\varphi )$
-conical points and by
![]() the set of
the set of
![]() $\varphi $
-conical points. We now establish the following dichotomy.
$\varphi $
-conical points. We now establish the following dichotomy.
Theorem 5.13.3. Assume
![]() $\mathbb {K}=\mathbb {R}$
and that
$\mathbb {K}=\mathbb {R}$
and that
![]() $\rho $
is Zariski-dense. If
$\rho $
is Zariski-dense. If
![]() $|\vartheta |\leq 2$
, then
$|\vartheta |\leq 2$
, then
![]() if
if
![]() $|\vartheta |\geq 4$
, then
$|\vartheta |\geq 4$
, then
![]()
Theorem 5.13.3 follows directly from Theorem 5.12.1 and the following proposition. Let us denote by
![]() the quotient projection.
the quotient projection.
Proposition 5.13.4. A point
![]() belongs to
belongs to
![]() if and only if for every pair
if and only if for every pair
![]() , one has
, one has
![]() ${{\mathsf {p}}}(x,y,v)\in \mathcal K({\unicode{x3c9} }^\varphi ).$
${{\mathsf {p}}}(x,y,v)\in \mathcal K({\unicode{x3c9} }^\varphi ).$
Proof. If
is such that
then consider
![]() $r{\kern-1pt}>{\kern-1pt}0$
and
$r{\kern-1pt}>{\kern-1pt}0$
and
![]() $\gamma _n{\kern-1pt}\to{\kern-1pt} y$
conically such that
$\gamma _n{\kern-1pt}\to{\kern-1pt} y$
conically such that
![]() $a((\gamma _n)_\rho )\in {\mathbb T}_r({\mathsf {u}}_\varphi ).$
By equation (30), there exists
$a((\gamma _n)_\rho )\in {\mathbb T}_r({\mathsf {u}}_\varphi ).$
By equation (30), there exists
![]() $\varepsilon $
given by Proposition 5.6.1 (only depending on
$\varepsilon $
given by Proposition 5.6.1 (only depending on
![]() $c_0$
and
$c_0$
and
![]() $c_1$
) such that for all n,
$c_1$
) such that for all n,
Consequently, equation (23) gives
By assumption,
![]() $a_\vartheta (\rho (\gamma _n))\in {\mathbb T}_r({\mathsf {u}}_\varphi )$
and one finds thus a divergent sequence
$a_\vartheta (\rho (\gamma _n))\in {\mathbb T}_r({\mathsf {u}}_\varphi )$
and one finds thus a divergent sequence
![]() $t_n\in \mathbb {R}_+$
such that
$t_n\in \mathbb {R}_+$
such that
for some
![]() $K'$
only depending on r and
$K'$
only depending on r and
![]() $\varepsilon .$
The sequence
$\varepsilon .$
The sequence
is thus contained in
for some
![]() $\kappa $
only depending on
$\kappa $
only depending on
in particular,
![]() ${{\mathsf {p}}}(x,y,v)\in \mathcal K({\unicode{x3c9} }^\varphi )$
as desired.
${{\mathsf {p}}}(x,y,v)\in \mathcal K({\unicode{x3c9} }^\varphi )$
as desired.
Reciprocally, if
belongs to
![]() $\mathcal K({\unicode{x3c9} }^\varphi ),$
let
$\mathcal K({\unicode{x3c9} }^\varphi ),$
let
![]() $\mathrm {B}$
be a bounded open set to which the
$\mathrm {B}$
be a bounded open set to which the
![]() ${\unicode{x3c9} }^\varphi $
-orbit of
${\unicode{x3c9} }^\varphi $
-orbit of
![]() ${{\mathsf {p}}}(x_0,y_0,v_0)$
returns to unbounded. Considering an accumulation point of the orbit points in
${{\mathsf {p}}}(x_0,y_0,v_0)$
returns to unbounded. Considering an accumulation point of the orbit points in
![]() $\mathrm {B}$
, we can assume that
$\mathrm {B}$
, we can assume that
![]() $\mathrm {B}={{\mathsf {p}}}(\tilde {\mathrm {B}})$
for some
$\mathrm {B}={{\mathsf {p}}}(\tilde {\mathrm {B}})$
for some
![]() $\tilde {\mathrm {B}}$
of the form
$\tilde {\mathrm {B}}$
of the form
We obtain thus divergent sequences
and
![]() $\{t_n\}\subset \mathbb {R}^+$
such that for all n,
$\{t_n\}\subset \mathbb {R}^+$
such that for all n,
Considering subsequences, we can assume that
![]() $\gamma _n^{-1}x_0\to x_\infty $
and
$\gamma _n^{-1}x_0\to x_\infty $
and
![]() $\gamma _n^{-1}y_0\to y_\infty .$
Necessarily,
$\gamma _n^{-1}y_0\to y_\infty .$
Necessarily,
![]() $x_\infty \neq y_\infty $
since they are at least
$x_\infty \neq y_\infty $
since they are at least
![]() $\kappa '$
apart. The sequence
$\kappa '$
apart. The sequence
![]() $\{\gamma _n\}$
is thus conical, but it is still to be determined whether it converges to
$\{\gamma _n\}$
is thus conical, but it is still to be determined whether it converges to
![]() $x_0$
or to
$x_0$
or to
![]() $y_0.$
$y_0.$
Using the last inequality in equation (33), we deduce, since
![]() $t_n\to +\infty ,$
that for all
$t_n\to +\infty ,$
that for all
![]() $\sigma \in \vartheta $
,
$\sigma \in \vartheta $
,
By definition of
![]() $\unicode{x3b2} _{}$
and the interpretation of the Buseman–Iwasawa cocycle via representations (equation (21)), one has
$\unicode{x3b2} _{}$
and the interpretation of the Buseman–Iwasawa cocycle via representations (equation (21)), one has
![]() $\log (\|\unicode{x3c6} _\sigma \rho (\gamma _n^{-1})v\|/\|v\|)\to -\infty $
for any non-vanishing
$\log (\|\unicode{x3c6} _\sigma \rho (\gamma _n^{-1})v\|/\|v\|)\to -\infty $
for any non-vanishing
![]() $v\in \Xi _{\unicode{x3c6} _\sigma }(\xi ^\vartheta (\gamma _n^{-1}y_0)),$
or equivalently, as
$v\in \Xi _{\unicode{x3c6} _\sigma }(\xi ^\vartheta (\gamma _n^{-1}y_0)),$
or equivalently, as
![]() $n\to \infty $
,
$n\to \infty $
,

We now use a standard linear algebra computation to conclude that
Lemma 5.13.5. (Bochi, Potrie, and Sambarino [Reference Bochi, Potrie and Sambarino10, Lemma A.3])
Let
![]() $A\in \operatorname {\mathrm {{\mathsf {GL}}}}_d(\mathbb {R})$
have a gap at
$A\in \operatorname {\mathrm {{\mathsf {GL}}}}_d(\mathbb {R})$
have a gap at
![]() $\alpha _1,$
then for every
$\alpha _1,$
then for every
![]() $v\in \mathbb {R}^d$
one has
$v\in \mathbb {R}^d$
one has
By Lemma 5.2.4, one concludes that
as
![]() $n\to \infty $
for all
$n\to \infty $
for all
![]() $\sigma \in \vartheta .$
Again by Lemma 5.2.4, one has
$\sigma \in \vartheta .$
Again by Lemma 5.2.4, one has
![]() $\gamma _n\to y_0$
as
$\gamma _n\to y_0$
as
![]() $n\to \infty $
(in
$n\to \infty $
(in
) and thus, by conicality of
![]() $\{\gamma _n\},$
that for all
$\{\gamma _n\},$
that for all
, it holds
![]() $\gamma _n^{-1}z\to x_\infty .$
It follows then that
$\gamma _n^{-1}z\to x_\infty .$
It follows then that
and, since
![]() $\gamma _n^{-1}y_0\to y_\infty \neq x_\infty ,$
that
$\gamma _n^{-1}y_0\to y_\infty \neq x_\infty ,$
that
Since the latter lower bound holds for all
![]() $\sigma \in \vartheta $
, one concludes that
$\sigma \in \vartheta $
, one concludes that
![]() $\xi ^\vartheta (\gamma _n^{-1}y_0)$
belongs to the Cartan basin
$\xi ^\vartheta (\gamma _n^{-1}y_0)$
belongs to the Cartan basin
![]() $B_{\vartheta ,\kappa "}(\rho (\gamma _n)).$
Thus, as in equation (31), one has
$B_{\vartheta ,\kappa "}(\rho (\gamma _n)).$
Thus, as in equation (31), one has
for some K only depending on
![]() $\kappa ".$
The latter, together with the second inequality from equation (33), implies that
$\kappa ".$
The latter, together with the second inequality from equation (33), implies that
![]() $y_0$
is
$y_0$
is
![]() $\varphi $
-conical, as desired.
$\varphi $
-conical, as desired.
Proof of Theorem 5.13.3
Consider a positive
![]() $\varepsilon .$
Fix
$\varepsilon .$
Fix
![]() and two neighborhoods
and two neighborhoods
![]() $A^-$
and
$A^-$
and
![]() $A^+$
of x and y, respectively, so that for all
$A^+$
of x and y, respectively, so that for all
![]() $(z,w)\in A^-,A^+$
, one has
$(z,w)\in A^-,A^+$
, one has
![]() $|[z,w]_\varphi -[x,y]_\varphi |<\varepsilon .$
Pick also an arbitrary
$|[z,w]_\varphi -[x,y]_\varphi |<\varepsilon .$
Pick also an arbitrary
![]() $T>0$
so that the quotient projection
$T>0$
so that the quotient projection
![]() ${{\mathsf {p}}}$
is injective on
${{\mathsf {p}}}$
is injective on
![]() $\tilde {\mathrm {B}}=A^-\times A^+\times B(0,T).$
We can thus compute the measure of
$\tilde {\mathrm {B}}=A^-\times A^+\times B(0,T).$
We can thus compute the measure of
![]() $\mathrm {B}={{\mathsf {p}}}(\tilde {\mathrm {B}})$
by equation (29).
$\mathrm {B}={{\mathsf {p}}}(\tilde {\mathrm {B}})$
by equation (29).
If we let
![]() $\tilde {\mathcal K}({\unicode{x3c9} }^\varphi )={{\mathsf {p}}}^{-1}(\mathcal K({\unicode{x3c9} }^\varphi )),$
then the lemma above asserts that
$\tilde {\mathcal K}({\unicode{x3c9} }^\varphi )={{\mathsf {p}}}^{-1}(\mathcal K({\unicode{x3c9} }^\varphi )),$
then the lemma above asserts that
If
![]() $|\vartheta |\leq 2$
, Theorem 5.12.1 states that
$|\vartheta |\leq 2$
, Theorem 5.12.1 states that
![]() $\Omega ^\varphi (\tilde {\mathrm {B}})=\Omega ^\varphi (\tilde {\mathcal K}({\unicode{x3c9} }^\varphi )\cap \tilde {\mathrm {B}}),$
which implies, up to
$\Omega ^\varphi (\tilde {\mathrm {B}})=\Omega ^\varphi (\tilde {\mathcal K}({\unicode{x3c9} }^\varphi )\cap \tilde {\mathrm {B}}),$
which implies, up to
![]() $e^{-\delta ^\varphi \varepsilon },$
that
$e^{-\delta ^\varphi \varepsilon },$
that
Since
![]() $\varepsilon $
is arbitrary, one concludes
$\varepsilon $
is arbitrary, one concludes
However, if
![]() $|\vartheta |\geq 4$
, then we have
$|\vartheta |\geq 4$
, then we have
![]() $\Omega ^\varphi (\tilde {\mathcal K}({\unicode{x3c9} }^\varphi ))=0$
, so
$\Omega ^\varphi (\tilde {\mathcal K}({\unicode{x3c9} }^\varphi ))=0$
, so
and the theorem is proved.
A Appendix. Ergodicity of skew-products with values on
 $\mathbb {R}$
$\mathbb {R}$
We freely use notation from Proposition 2.4.2 which we intend to prove. The proof presented here is mainly a collection of results.
We say that
![]() ${\mathsf {K}}$
is recurrent if for every measurable set
${\mathsf {K}}$
is recurrent if for every measurable set
![]() $A\subset \Sigma $
with
$A\subset \Sigma $
with
![]() $\nu (A)>0$
and every neighborhood
$\nu (A)>0$
and every neighborhood
![]() $N(0)$
of
$N(0)$
of
![]() $0$
in V, there exists
$0$
in V, there exists
![]() $n\in \mathbb {Z}-\{0\}$
such that one has
$n\in \mathbb {Z}-\{0\}$
such that one has
 $$ \begin{align*}\nu\bigg(A\cap\sigma^{-n}A\cap\{x:\sum_{k=0}^n{\mathsf{K}}(\sigma^ix)\in N(0)\}\bigg)>0.\end{align*} $$
$$ \begin{align*}\nu\bigg(A\cap\sigma^{-n}A\cap\{x:\sum_{k=0}^n{\mathsf{K}}(\sigma^ix)\in N(0)\}\bigg)>0.\end{align*} $$
It is proven by Schmidt [Reference Schmidt67, Theorem 5.5] that
![]() ${\mathsf {K}}$
is recurrent if and only if the skew-product
${\mathsf {K}}$
is recurrent if and only if the skew-product
![]() $f^{\mathsf {K}}:\Sigma \times \mathbb {R}\to \Sigma \times \mathbb {R}$
is conservative (see Aaronson’s book [Reference Aaronson1, §1.1] for the definition). It is moreover a general fact that mean-zero cocycles over the reals are conservative, see [Reference Aaronson1, Corollary 8.1.5] from which we state here a particular case.
$f^{\mathsf {K}}:\Sigma \times \mathbb {R}\to \Sigma \times \mathbb {R}$
is conservative (see Aaronson’s book [Reference Aaronson1, §1.1] for the definition). It is moreover a general fact that mean-zero cocycles over the reals are conservative, see [Reference Aaronson1, Corollary 8.1.5] from which we state here a particular case.
Corollary A.1. Since, by assumption,
![]() $\int {\mathsf {K}}\,d\nu =0,$
the cocycle
$\int {\mathsf {K}}\,d\nu =0,$
the cocycle
![]() $f^{\mathsf {K}}$
is conservative and so
$f^{\mathsf {K}}$
is conservative and so
![]() ${\mathsf {K}}$
is recurrent.
${\mathsf {K}}$
is recurrent.
The proof of Proposition 2.4.2 ends with the following theorem of Coelho (obtained by the combination of Example 2.4 and Corollary 3.4 of Coelho [Reference Coelho26]), specific to sub-shifts and equilibrium states.
Theorem A.0.1. (Coelho [Reference Coelho26])
Assume
![]() ${\mathsf {K}}$
is non-arithmetic and let
${\mathsf {K}}$
is non-arithmetic and let
![]() $\nu $
be an equilibrium state of
$\nu $
be an equilibrium state of
![]() $\sigma $
for a Hölder potential. Then, f is ergodic with respect to
$\sigma $
for a Hölder potential. Then, f is ergodic with respect to
![]() if and only if
if and only if
![]() ${\mathsf {K}}$
is recurrent.
${\mathsf {K}}$
is recurrent.
B Appendix. Mixing
In this appendix, we give a quick outline of the proof of Theorem 2.5.2. We use small modifications of classical computations performed by Babillot [Reference Babillot3] as well as by Babillot and Ledrappier [Reference Babillot and Ledrappier5], Ledrappier and Sarig [Reference Ledrappier and Sarig45], and more recently by Oh and Pan [Reference Oh and Pan52] and Chow and Sarkar [Reference Chow and Sarkar25], where an extra parameter (an holonomy with values on a compact group) has been added to the Ruelle operator. We thank M. Chow and P. Sarkar for pointing out an issue in the argument presented by Sambarino [Reference Sambarino66], Ledrappier for suggesting the reference [Reference Ledrappier and Sarig45], and Oh for pinpointing the reference [Reference Oh and Pan52].
It is first convenient to straighten the flow action by means of twisting the r-action.
Lemma B.1. Let
![]() $U=\mathbb {R}\times W,$
and let
$U=\mathbb {R}\times W,$
and let
![]() $k:\Sigma \to U$
be
$k:\Sigma \to U$
be
![]() $k(x)=(r(x),\int _0^{r(x)}K(x,s)\,ds),$
then:
$k(x)=(r(x),\int _0^{r(x)}K(x,s)\,ds),$
then:
-
• there exists
 $\varphi \in U^*$
such that
$\varphi \in U^*$
such that
 $\varphi (k)=r>0,$
$\varphi (k)=r>0,$
-
•
 $\int kd\nu =(\int rd\nu ,0)\neq 0;$
$\int kd\nu =(\int rd\nu ,0)\neq 0;$
-
• there exists a bi-Hölder homeomorphism
 where which is a measurable isomorphism between
where which is a measurable isomorphism between $$ \begin{align*}\hat k(x,u)=(\sigma(x),u-k(x)),\end{align*} $$
$$ \begin{align*}\hat k(x,u)=(\sigma(x),u-k(x)),\end{align*} $$
 and
and
 $\nu \otimes \operatorname {\mathrm {Leb}}_U{\kern-3pt}/\hat k,$
that conjugates
$\nu \otimes \operatorname {\mathrm {Leb}}_U{\kern-3pt}/\hat k,$
that conjugates
 $\psi $
with the flow induced on the quotient by where
$\psi $
with the flow induced on the quotient by where $$ \begin{align*}(x,u)\mapsto(x,u-t\tau),\end{align*} $$
$$ \begin{align*}(x,u)\mapsto(x,u-t\tau),\end{align*} $$
 $\tau \in \int kd\nu $
is such that
$\tau \in \int kd\nu $
is such that
 $\varphi (\tau )=1.$
$\varphi (\tau )=1.$
Proof. Define
![]() by
by
![]() $E((x,t),w)=(x,(t,w+\int _0^tK(x,s)\,ds)).$
It is well defined since the above formula is equivariant. Indeed, one has
$E((x,t),w)=(x,(t,w+\int _0^tK(x,s)\,ds)).$
It is well defined since the above formula is equivariant. Indeed, one has
 $$ \begin{align*}\int_0^{t-r(x)}K(\sigma(x),s)\,ds & = \int_{r(x)}^{t}K(\sigma(x),s-r(x))\,ds & \\ & = \int_{r(x)}^{t}K(x,s)\,ds &\quad(K\textrm{ is }\hat r\textrm{-invariant})\\ & = \int_{0}^{t}K(x,s)\,ds-\int_0^{r(x)}K(x,s)\,ds, & \end{align*} $$
$$ \begin{align*}\int_0^{t-r(x)}K(\sigma(x),s)\,ds & = \int_{r(x)}^{t}K(\sigma(x),s-r(x))\,ds & \\ & = \int_{r(x)}^{t}K(x,s)\,ds &\quad(K\textrm{ is }\hat r\textrm{-invariant})\\ & = \int_{0}^{t}K(x,s)\,ds-\int_0^{r(x)}K(x,s)\,ds, & \end{align*} $$
which implies
 $$ \begin{align*} E(\hat r(x,t),w) & =\bigg(\sigma(x),(t-r(x),w+\int_0^{t-r(x)}K(\sigma(x),s)\,ds)\bigg)\\ & = \bigg(\sigma(x),(t-r(x),w+\int_{0}^{t}K(x,s)\,ds-\int_0^{r(x)}K(x,s)\,ds)\bigg)\\ & =\hat k(E((x,t),w)), \end{align*} $$
$$ \begin{align*} E(\hat r(x,t),w) & =\bigg(\sigma(x),(t-r(x),w+\int_0^{t-r(x)}K(\sigma(x),s)\,ds)\bigg)\\ & = \bigg(\sigma(x),(t-r(x),w+\int_{0}^{t}K(x,s)\,ds-\int_0^{r(x)}K(x,s)\,ds)\bigg)\\ & =\hat k(E((x,t),w)), \end{align*} $$
as desired. The remaining assertions follow similarly.
We will work from now on with this latter flow, still denoted by
![]() $\psi $
so as not to overcharge with notation. Up to Livšic-cohomology, we may assume that k is defined on
$\psi $
so as not to overcharge with notation. Up to Livšic-cohomology, we may assume that k is defined on
![]() $\Sigma ^+.$
$\Sigma ^+.$
By measure-theoretic arguments, we consider
![]() $F,G:\Sigma ^+\times U\to \mathbb {R}$
that we can assume have separated variables, that is, can be written as
$F,G:\Sigma ^+\times U\to \mathbb {R}$
that we can assume have separated variables, that is, can be written as
![]() $F(x,u)=p_F(x)v_F(u),$
with
$F(x,u)=p_F(x)v_F(u),$
with
![]() $p_F$
and
$p_F$
and
![]() $p_G$
Hölder-continuous, and
$p_G$
Hölder-continuous, and
![]() $v_F$
and
$v_F$
and
![]() $v_G$
smooth with compact support. We have to show that, as
$v_G$
smooth with compact support. We have to show that, as
![]() $t\to \infty ,$
$t\to \infty ,$
Tracing back the definitions, one is brought up to understanding the limit as
![]() $t\to \infty $
of
$t\to \infty $
of
 $$ \begin{align}t^{\dim W/2}\bigg(\int_{\Sigma^+\times U}\sum_{n\in\mathbb{N}}F(x,u)G(\sigma^nx,u-S_nk(x)-t\tau)\,d\nu \,d\operatorname{\mathrm{Leb}}_U\bigg),\end{align} $$
$$ \begin{align}t^{\dim W/2}\bigg(\int_{\Sigma^+\times U}\sum_{n\in\mathbb{N}}F(x,u)G(\sigma^nx,u-S_nk(x)-t\tau)\,d\nu \,d\operatorname{\mathrm{Leb}}_U\bigg),\end{align} $$
where
![]() $S_nk(x)=\sum _{i=0}^nk(\sigma ^i(x))$
is the Birkhoff sum. We focus on the integral between brackets, only to multiply at the very end of our computation by
$S_nk(x)=\sum _{i=0}^nk(\sigma ^i(x))$
is the Birkhoff sum. We focus on the integral between brackets, only to multiply at the very end of our computation by
![]() $\sqrt {t}^{d-1},$
where
$\sqrt {t}^{d-1},$
where
![]() $d=\dim U.$
The above integral becomes
$d=\dim U.$
The above integral becomes
 $$ \begin{align*}\int_{\Sigma^+\times U}\sum_{n\in\mathbb{N}}p_F(x)p_G(\sigma^nx)v_F(u)v_G(u-S_nk(x)-t\tau)\,d\nu(x) \,d\operatorname{\mathrm{Leb}}_U(u).\end{align*} $$
$$ \begin{align*}\int_{\Sigma^+\times U}\sum_{n\in\mathbb{N}}p_F(x)p_G(\sigma^nx)v_F(u)v_G(u-S_nk(x)-t\tau)\,d\nu(x) \,d\operatorname{\mathrm{Leb}}_U(u).\end{align*} $$
Recall that, by assumption, there is
![]() $\varphi {\kern-1pt}\in{\kern-1pt} U^*$
so that
$\varphi {\kern-1pt}\in{\kern-1pt} U^*$
so that
![]() $\varphi (k)=hr{\kern-1pt}>{\kern-1pt}0$
and that
$\varphi (k)=hr{\kern-1pt}>{\kern-1pt}0$
and that
![]() $P(-hr)=0,$
so up to Livšic-cohomology, we can assume that
$P(-hr)=0,$
so up to Livšic-cohomology, we can assume that
![]() $-\varphi (k)=-hr$
is normalized, that is, so that the Ruelle operator, defined by
$-\varphi (k)=-hr$
is normalized, that is, so that the Ruelle operator, defined by
 $$ \begin{align*}\mathcal L_{\varphi}\Phi(x)=\sum_{y:\sigma(y)=x}e^{-\varphi(k(y))}\Phi(y),\end{align*} $$
$$ \begin{align*}\mathcal L_{\varphi}\Phi(x)=\sum_{y:\sigma(y)=x}e^{-\varphi(k(y))}\Phi(y),\end{align*} $$
verifies
![]() $\mathcal L_{\varphi }^*\nu =\nu ,$
in particular, for every pair of Hölder-continuous functions
$\mathcal L_{\varphi }^*\nu =\nu ,$
in particular, for every pair of Hölder-continuous functions
![]() $j,l$
on
$j,l$
on
![]() $\Sigma ^+$
, one has
$\Sigma ^+$
, one has
![]() $\int _{\Sigma ^+}j(\sigma x)l(x)\,d\nu =\int _{\Sigma ^+}j(x)(\mathcal L_{\varphi }l)(x)\,d\nu .$
$\int _{\Sigma ^+}j(\sigma x)l(x)\,d\nu =\int _{\Sigma ^+}j(x)(\mathcal L_{\varphi }l)(x)\,d\nu .$
Denote by
![]() $\operatorname {\mathrm {Leb}}_{U^*}$
the Lebesgue measure on
$\operatorname {\mathrm {Leb}}_{U^*}$
the Lebesgue measure on
![]() $U^*$
defined by the Fourier inversion formula
$U^*$
defined by the Fourier inversion formula
for the Fourier transform
![]() $\mathcal Fv_G$
if
$\mathcal Fv_G$
if
![]() $v_G.$
As in [Reference Babillot and Ledrappier5, §2.3] we can, and will, assume that
$v_G.$
As in [Reference Babillot and Ledrappier5, §2.3] we can, and will, assume that
![]() $\mathcal F v_G$
is of class
$\mathcal F v_G$
is of class
![]() $\operatorname {\mathrm {C}}^N$
for some
$\operatorname {\mathrm {C}}^N$
for some
![]() $N>(d-1)/2$
and has compact support.
$N>(d-1)/2$
and has compact support.
We will suppress the notation
![]() $\nu , \operatorname {\mathrm {Leb}}_U$
, and
$\nu , \operatorname {\mathrm {Leb}}_U$
, and
![]() $\operatorname {\mathrm {Leb}}_{U^*}$
from the integrals from now on. The desired integral, equation (B.1), then becomes
$\operatorname {\mathrm {Leb}}_{U^*}$
from the integrals from now on. The desired integral, equation (B.1), then becomes
 $$ \begin{align} & \int_{\Sigma^+\times U}\sum_{n\in\mathbb{N}}(\mathcal L_{\varphi}^np_F)(x)p_G(x)v_F(u)v_G(u-S_nk(x)-t\tau)\,dx \,du\nonumber\\&\quad = \int_{\Sigma^+\times U}\sum_{n\in\mathbb{N}}(\mathcal L_{\varphi}^np_F)(x)p_G(x)v_F(u)\int_{U^*}e^{i\psi(u-S_nk(x)-t\tau)}\mathcal Fv_G(\psi)\,d\psi \,dx \,du,\nonumber\\&\quad = \int_{\Sigma^+\times U}\int_{U^*}\sum_{n\in\mathbb{N}}(\mathcal L_{\varphi+i\psi}^np_F)(x)p_G(x)v_F(u)e^{i\psi(u-t\tau)}\mathcal Fv_G(\psi)\,d\psi \,dx \,du \nonumber\\&\quad = \int_{\Sigma^+\times U}p_G(x)v_F(u)\int_{U^*}\sum_{n\in\mathbb{N}}(\mathcal L_{\varphi+i\psi}^np_F)(x)e^{i\psi(u-t\tau)}\mathcal Fv_G(\psi)\,d\psi \,dx \,du. \end{align} $$
$$ \begin{align} & \int_{\Sigma^+\times U}\sum_{n\in\mathbb{N}}(\mathcal L_{\varphi}^np_F)(x)p_G(x)v_F(u)v_G(u-S_nk(x)-t\tau)\,dx \,du\nonumber\\&\quad = \int_{\Sigma^+\times U}\sum_{n\in\mathbb{N}}(\mathcal L_{\varphi}^np_F)(x)p_G(x)v_F(u)\int_{U^*}e^{i\psi(u-S_nk(x)-t\tau)}\mathcal Fv_G(\psi)\,d\psi \,dx \,du,\nonumber\\&\quad = \int_{\Sigma^+\times U}\int_{U^*}\sum_{n\in\mathbb{N}}(\mathcal L_{\varphi+i\psi}^np_F)(x)p_G(x)v_F(u)e^{i\psi(u-t\tau)}\mathcal Fv_G(\psi)\,d\psi \,dx \,du \nonumber\\&\quad = \int_{\Sigma^+\times U}p_G(x)v_F(u)\int_{U^*}\sum_{n\in\mathbb{N}}(\mathcal L_{\varphi+i\psi}^np_F)(x)e^{i\psi(u-t\tau)}\mathcal Fv_G(\psi)\,d\psi \,dx \,du. \end{align} $$
We seek thus to understand the nature of
![]() $\psi \mapsto \sum _{n\in \mathbb {N}}\mathcal L_{\varphi +i\psi }^n,$
for which one is brought to understand the spectral radius
$\psi \mapsto \sum _{n\in \mathbb {N}}\mathcal L_{\varphi +i\psi }^n,$
for which one is brought to understand the spectral radius
![]() ${{\mathsf {r}}}_\psi $
of
${{\mathsf {r}}}_\psi $
of
![]() $\mathcal L_{\varphi +i\psi }.$
Applying [Reference Parry and Pollicott53, Ch. 4], we obtain that for every
$\mathcal L_{\varphi +i\psi }.$
Applying [Reference Parry and Pollicott53, Ch. 4], we obtain that for every
![]() $\psi \in U^*$
, one has
$\psi \in U^*$
, one has
![]() ${{\mathsf {r}}}_\psi \in (0,1].$
We then distinguish two situations.
${{\mathsf {r}}}_\psi \in (0,1].$
We then distinguish two situations.
The spectral radius
![]() ${{\mathsf {r}}}_\psi $
is smaller than
${{\mathsf {r}}}_\psi $
is smaller than
![]() $1.$
In which case
$1.$
In which case
is analytic on a neighborhood of
![]() $\psi .$
$\psi .$
The spectral radius
![]() ${{\mathsf {r}}}_\psi $
equals
${{\mathsf {r}}}_\psi $
equals
![]() $1.$
One has then the following theorem.
$1.$
One has then the following theorem.
Theorem B.1. (Parry and Pollicott [Reference Parry and Pollicott53, Ch. 4])
One has
![]() ${{\mathsf {r}}}_\psi =1$
if and only if there exists a Hölder-continuous
${{\mathsf {r}}}_\psi =1$
if and only if there exists a Hölder-continuous
![]() $w_\psi :\Sigma ^+\to \mathbb {S}^1$
such that for all
$w_\psi :\Sigma ^+\to \mathbb {S}^1$
such that for all
![]() $x\in \Sigma ^+$
, one has
$x\in \Sigma ^+$
, one has

In this situation, the function
![]() $w_\psi $
is unique up to scalars.
$w_\psi $
is unique up to scalars.
Applying moreover [Reference Parry and Pollicott53, Theorem 4.5] and the perturbation theorem [Reference Parry and Pollicott53, Proposition 4.6], there exists a neighborhood
![]() $\mathcal O_\psi $
of
$\mathcal O_\psi $
of
![]() $\psi $
such that for all
$\psi $
such that for all
![]() $\eta \in \mathcal O_\psi $
, one has
$\eta \in \mathcal O_\psi $
, one has
where
![]() $Q_\eta $
is a rank-one projector,
$Q_\eta $
is a rank-one projector,
![]() $N_\eta $
is an operator with spectral radius strictly smaller than
$N_\eta $
is an operator with spectral radius strictly smaller than
![]() ${{\mathsf {r}}}_\eta =|\unicode{x3bb} _\eta |$
, and such that
${{\mathsf {r}}}_\eta =|\unicode{x3bb} _\eta |$
, and such that
![]() $Q_\eta N_\eta =N_\eta Q_\eta =0.$
The above objects are analytic on
$Q_\eta N_\eta =N_\eta Q_\eta =0.$
The above objects are analytic on
![]() $\mathcal O_\psi .$
The operator
$\mathcal O_\psi .$
The operator
![]() $M_\psi =\sum _{n\in \mathbb {N}}N_\psi ^n$
is hence well defined and analytic on
$M_\psi =\sum _{n\in \mathbb {N}}N_\psi ^n$
is hence well defined and analytic on
![]() $\mathcal O_\psi .$
Observe that, as we have assumed
$\mathcal O_\psi .$
Observe that, as we have assumed
![]() $-\varphi (k)$
to be normalized, one has
$-\varphi (k)$
to be normalized, one has
 $$ \begin{align}Q_0(f)(x)=\bigg(\int_{\Sigma^+}fd\nu\bigg)\cdot 1.\end{align} $$
$$ \begin{align}Q_0(f)(x)=\bigg(\int_{\Sigma^+}fd\nu\bigg)\cdot 1.\end{align} $$
Remark B.2. Since k has a dense group of periods on
![]() $U, \psi (k):\Sigma ^+\to \mathbb {R}$
has a dense group of periods as soon as
$U, \psi (k):\Sigma ^+\to \mathbb {R}$
has a dense group of periods as soon as
![]() $\psi \neq 0,$
and [Reference Parry and Pollicott53, Theorem 4.5] implies that
$\psi \neq 0,$
and [Reference Parry and Pollicott53, Theorem 4.5] implies that
![]() $\{\unicode{x3bb} _\psi ^n:n\in \mathbb {Z}\}$
is dense in
$\{\unicode{x3bb} _\psi ^n:n\in \mathbb {Z}\}$
is dense in
![]() $\mathbb {S}^1=\partial \mathbb {D}.$
In particular,
$\mathbb {S}^1=\partial \mathbb {D}.$
In particular,
![]() $\unicode{x3bb} _\psi \neq 1,$
unless
$\unicode{x3bb} _\psi \neq 1,$
unless
![]() $\psi =0.$
Consequently, if
$\psi =0.$
Consequently, if
![]() $\psi \neq 0$
, then for all
$\psi \neq 0$
, then for all
![]() $\eta \in \mathcal O_\psi $
, the operator
$\eta \in \mathcal O_\psi $
, the operator

is well defined and analytic on
![]() $\mathcal O_\psi .$
$\mathcal O_\psi .$
Lemma B.3. If
![]() ${{\mathsf {r}}}_\psi =1$
, then for all
${{\mathsf {r}}}_\psi =1$
, then for all
![]() $\eta \in \mathcal O_\psi -\{\psi \}$
, it holds
$\eta \in \mathcal O_\psi -\{\psi \}$
, it holds
![]() ${{\mathsf {r}}}_\eta <1.$
Consequently,
${{\mathsf {r}}}_\eta <1.$
Consequently,

is analytic on
![]() $\mathcal O_\psi -\{\psi \}$
and, if
$\mathcal O_\psi -\{\psi \}$
and, if
![]() $\psi \neq 0,$
it extends analytically to
$\psi \neq 0,$
it extends analytically to
![]() $\mathcal O_\psi ,$
as the right-hand-side of the equation is well defined on
$\mathcal O_\psi ,$
as the right-hand-side of the equation is well defined on
![]() $\psi .$
$\psi .$
Proof. As
![]() $\eta \mapsto \unicode{x3bb} _\eta $
is analytic on
$\eta \mapsto \unicode{x3bb} _\eta $
is analytic on
![]() $\mathcal O_\psi ,$
together with the above density result, it follows that there is a neighborhood (possibly smaller but) still denoted by
$\mathcal O_\psi ,$
together with the above density result, it follows that there is a neighborhood (possibly smaller but) still denoted by
![]() $\mathcal O_\psi $
such that if
$\mathcal O_\psi $
such that if
![]() $|\unicode{x3bb} _\eta |=1$
, then
$|\unicode{x3bb} _\eta |=1$
, then
![]() $\unicode{x3bb} _\eta =\unicode{x3bb} _\psi .$
One has then, applying Theorem B.1, that
$\unicode{x3bb} _\eta =\unicode{x3bb} _\psi .$
One has then, applying Theorem B.1, that

The remark and Theorem B.1 give
![]() $\psi -\eta =0$
and so the lemma is established.
$\psi -\eta =0$
and so the lemma is established.
One obtains then that the operator
![]() $\sum _{n\in \mathbb {N}}\mathcal L_{\varphi +i\psi }^n$
is well defined and varies analytically on
$\sum _{n\in \mathbb {N}}\mathcal L_{\varphi +i\psi }^n$
is well defined and varies analytically on
![]() $\psi $
except at
$\psi $
except at
![]() $\psi =0.$
One is thus taken to localize the integral in equation (B.2) about
$\psi =0.$
One is thus taken to localize the integral in equation (B.2) about
![]() $0.$
To that end, one considers an auxiliary
$0.$
To that end, one considers an auxiliary
![]() $\operatorname {\mathrm {C}}^\infty $
function
$\operatorname {\mathrm {C}}^\infty $
function
![]() $\kappa :U^*\to \mathbb {R},$
supported on the neighborhood
$\kappa :U^*\to \mathbb {R},$
supported on the neighborhood
![]() $\mathcal O_0$
, where equation (B.3) holds, with
$\mathcal O_0$
, where equation (B.3) holds, with
![]() $\kappa (0)=1,$
and we seek to understand the modified integral over
$\kappa (0)=1,$
and we seek to understand the modified integral over
![]() $U^*$
on equation (B.2) given, for
$U^*$
on equation (B.2) given, for
![]() $(x,u)\in \Sigma ^+\times U,$
by
$(x,u)\in \Sigma ^+\times U,$
by
 $$ \begin{align}\int_{U^*}(1-\kappa(\psi))\sum_{n\in\mathbb{N}}(\mathcal L_{\varphi+i\psi}^np_F)(x)e^{i\psi(u-t\tau)}\mathcal Fv_G(\psi)\,d\psi.\end{align} $$
$$ \begin{align}\int_{U^*}(1-\kappa(\psi))\sum_{n\in\mathbb{N}}(\mathcal L_{\varphi+i\psi}^np_F)(x)e^{i\psi(u-t\tau)}\mathcal Fv_G(\psi)\,d\psi.\end{align} $$
Consider from §2.6 the critical hypersurface
![]() $\mathcal Q_{k}\subset U^*.$
It follows from Babillot and Ledrappier [Reference Babillot and Ledrappier5] that one has
$\mathcal Q_{k}\subset U^*.$
It follows from Babillot and Ledrappier [Reference Babillot and Ledrappier5] that one has
![]() $\mathcal Q_{k}=\mathbf {P}^{-1}(0)$
and the tangent space
$\mathcal Q_{k}=\mathbf {P}^{-1}(0)$
and the tangent space
![]() ${\mathsf {T}}_\varphi \mathcal Q_{k}=\{\psi \in U^*:\psi (\tau )=0\}.$
For
${\mathsf {T}}_\varphi \mathcal Q_{k}=\{\psi \in U^*:\psi (\tau )=0\}.$
For
![]() $\psi \in U^*$
, let
$\psi \in U^*$
, let
be its decomposition along
![]() $U^*=\mathbb {R}\varphi \oplus {\mathsf {T}}_\varphi \mathcal Q_{k}.$
Decomposing
$U^*=\mathbb {R}\varphi \oplus {\mathsf {T}}_\varphi \mathcal Q_{k}.$
Decomposing
![]() $\,d\psi $
as
$\,d\psi $
as
![]() $dsd\psi _0,$
the integral in equation (B.5) becomes
$dsd\psi _0,$
the integral in equation (B.5) becomes
 $$ \begin{align}\int_{\mathbb{R}}e^{-its}\int_{\mathsf{T_\varphi\mathcal Q_{k}}}e^{i\psi(u)}(1-\kappa(\psi))\sum_{n\in\mathbb{N}}(\mathcal L_{\varphi+i\psi}^np_F)(x)\mathcal Fv_G(\psi)\,d\psi_0\,ds=O(t^{-N})\end{align} $$
$$ \begin{align}\int_{\mathbb{R}}e^{-its}\int_{\mathsf{T_\varphi\mathcal Q_{k}}}e^{i\psi(u)}(1-\kappa(\psi))\sum_{n\in\mathbb{N}}(\mathcal L_{\varphi+i\psi}^np_F)(x)\mathcal Fv_G(\psi)\,d\psi_0\,ds=O(t^{-N})\end{align} $$
as it is the Fourier transform of the integral over
![]() ${\mathsf {T}}_\varphi \mathcal Q_{k},$
which is, by Lemma B.3, as regular as
${\mathsf {T}}_\varphi \mathcal Q_{k},$
which is, by Lemma B.3, as regular as
![]() $\mathcal Fv_G(\psi ),$
and this function was chosen to be of class
$\mathcal Fv_G(\psi ),$
and this function was chosen to be of class
![]() $\operatorname {\mathrm {C}}^N$
for some
$\operatorname {\mathrm {C}}^N$
for some
![]() $N>(d-1)/2.$
$N>(d-1)/2.$
We can thus focus on the integral from equation (B.2) localized about 0, so it becomes, using again Lemma B.3,

We first treat the term containing
![]() $M_\psi ,$
which is dealt with as we did with equation (B.5). Indeed, for the same reasons, one has for all
$M_\psi ,$
which is dealt with as we did with equation (B.5). Indeed, for the same reasons, one has for all
![]() $(x,u)\in \Sigma ^+\times U,$
the integral
$(x,u)\in \Sigma ^+\times U,$
the integral
 $$ \begin{align} & \int_{U^*}\kappa(\psi)(M_\psi p_F)(x)e^{i\psi(u-t\tau)} \mathcal Fv_G(\psi)\,d\psi \nonumber \\ &\quad=\int_{\mathbb{R}}e^{-its}\int_{\mathsf{T_\varphi\mathcal Q_{k}}}e^{i\psi(u)}\kappa(\psi)(M_\psi p_F)(x) \mathcal Fv_G(\psi)\,d\psi_0\,ds \nonumber\\ &\quad= O(t^{-N}).\end{align} $$
$$ \begin{align} & \int_{U^*}\kappa(\psi)(M_\psi p_F)(x)e^{i\psi(u-t\tau)} \mathcal Fv_G(\psi)\,d\psi \nonumber \\ &\quad=\int_{\mathbb{R}}e^{-its}\int_{\mathsf{T_\varphi\mathcal Q_{k}}}e^{i\psi(u)}\kappa(\psi)(M_\psi p_F)(x) \mathcal Fv_G(\psi)\,d\psi_0\,ds \nonumber\\ &\quad= O(t^{-N}).\end{align} $$
We attempt then to understand the integral

the issue being the singularity at
![]() $\psi =0$
of
$\psi =0$
of
![]() $1/(1-\unicode{x3bb} _\psi ).$
To that end, consider the function
$1/(1-\unicode{x3bb} _\psi ).$
To that end, consider the function
![]() $\mathbf {Q}: {\mathsf {T}}_\varphi \mathcal Q_{k}\to \mathbb {R}$
defined implicitly by the equation
$\mathbf {Q}: {\mathsf {T}}_\varphi \mathcal Q_{k}\to \mathbb {R}$
defined implicitly by the equation
It is analytic, critical at 0 with
![]() $\mathbf {Q}(0)=1,$
and has positive-definite Hessian at 0,
$\mathbf {Q}(0)=1,$
and has positive-definite Hessian at 0,
![]() $\operatorname {\mathrm {Hess}}_0\mathbf {Q}.$
Using Taylor expansion, one writes
$\operatorname {\mathrm {Hess}}_0\mathbf {Q}.$
Using Taylor expansion, one writes
One applies the Weierstrass preparation theorem [Reference Hörmander38, Theorem 7.5.1] to express
![]() $1-\unicode{x3bb} _\psi $
about
$1-\unicode{x3bb} _\psi $
about
![]() $0$
as
$0$
as
(recall the decomposition of
![]() $\psi $
from equation (B.6)) where a is real-analytic and
$\psi $
from equation (B.6)) where a is real-analytic and
![]() $a(0)=h\int rd\nu $
(see [Reference Babillot and Ledrappier5, p. 37] or [Reference Ledrappier and Sarig45, p. 17] for details). Whence, as in [Reference Babillot and Ledrappier5, Lemma 2.3], using the formula
$a(0)=h\int rd\nu $
(see [Reference Babillot and Ledrappier5, p. 37] or [Reference Ledrappier and Sarig45, p. 17] for details). Whence, as in [Reference Babillot and Ledrappier5, Lemma 2.3], using the formula
![]() $1/z=-\int _0^\infty e^{Tz}dT$
, one has
$1/z=-\int _0^\infty e^{Tz}dT$
, one has

and equation (B.10) becomes, denoting
![]() $C(\psi ,x)=\kappa (\psi ){(Q_\psi p_F)(x)}/{a(\psi )}\mathcal Fv_G(\psi )$
to lighten the notation,
$C(\psi ,x)=\kappa (\psi ){(Q_\psi p_F)(x)}/{a(\psi )}\mathcal Fv_G(\psi )$
to lighten the notation,
 $$ \begin{align} & \int_{U^*}\!e^{i\psi(u-t\tau)}\kappa(\psi)\frac{(Q_\psi p_F)(x)}{a(\psi)}\mathcal Fv_G(\psi)\int_0^\infty e^{T(is_\psi-(1/2)\operatorname{\mathrm{Hess}}_0\mathbf{Q}(\psi_0)-O(\|\psi_0\|^2))}\,dT \,d\psi_0\,ds \nonumber\\ &\quad=\int_0^\infty\int_{\mathbb{R}}e^{-i(t-T)s}\int_{\mathsf{T_\varphi\mathcal Q_{k}}}C(\psi,x)e^{i\psi(u)-T(\operatorname{\mathrm{Hess}}_0\mathbf{Q}(\psi_0)/2+O(\|\psi_0\|^2))} \,d\psi_0\,ds\,dT. \end{align} $$
$$ \begin{align} & \int_{U^*}\!e^{i\psi(u-t\tau)}\kappa(\psi)\frac{(Q_\psi p_F)(x)}{a(\psi)}\mathcal Fv_G(\psi)\int_0^\infty e^{T(is_\psi-(1/2)\operatorname{\mathrm{Hess}}_0\mathbf{Q}(\psi_0)-O(\|\psi_0\|^2))}\,dT \,d\psi_0\,ds \nonumber\\ &\quad=\int_0^\infty\int_{\mathbb{R}}e^{-i(t-T)s}\int_{\mathsf{T_\varphi\mathcal Q_{k}}}C(\psi,x)e^{i\psi(u)-T(\operatorname{\mathrm{Hess}}_0\mathbf{Q}(\psi_0)/2+O(\|\psi_0\|^2))} \,d\psi_0\,ds\,dT. \end{align} $$
Using Taylor series on the
![]() $\psi $
-variable, we may, and will, assume that
$\psi $
-variable, we may, and will, assume that
![]() $C(\psi ,x)$
is of the form
$C(\psi ,x)$
is of the form
![]() $c_x(s_\psi )b(\psi _0).$
Equation (B.11) now becomes
$c_x(s_\psi )b(\psi _0).$
Equation (B.11) now becomes
 $$ \begin{align} &\int_0^\infty\int_{\mathbb{R}}e^{-i(t-T-\varphi(u))s}c_{x}(s)\,ds\int_{\mathsf{T_\varphi\mathcal Q_{k}}}b(\psi_0)e^{i\psi_0(u)-T(\operatorname{\mathrm{Hess}}_0\mathbf{Q}(\psi_0)/2+O(\|\psi_0\|^2))} \,d\psi_0\,dT \nonumber \\&\quad= \int_0^\infty \mathcal F c_{x}(t-T-\varphi(u))\int_{\mathsf{T_\varphi\mathcal Q_{k}}}b(\psi_0)e^{i\psi_0(u)-T(\operatorname{\mathrm{Hess}}_0\mathbf{Q}(\psi_0)/2+O(\|\psi_0\|^2))} \,d\psi_0\,dT \nonumber\\ &\quad= \int_{\varphi(u)}^\infty\mathcal F c_{x}(t-T)\int_{\mathsf{T_\varphi\mathcal Q_{k}}}b(\psi_0)e^{i\psi_0(u)-(T-\varphi(u))(\operatorname{\mathrm{Hess}}_0\mathbf{Q}(\psi_0)/2+O(\|\psi_0\|^2))} \,d\psi_0\,dT,\nonumber\\ &\quad=\int_{\max(t/2,\varphi(u))}^\infty\mathcal F c_{x}(t-T)\nonumber\\ &\ \qquad \times \int_{\mathsf{T_\varphi\mathcal Q_{k}}}b(\psi_0)e^{i\psi_0(u)-(T-\varphi(u))(\operatorname{\mathrm{Hess}}_0\mathbf{Q}(\psi_0)/2+O(\|\psi_0\|^2))} d\psi_0\,dT+O(t^{-N}), \end{align} $$
$$ \begin{align} &\int_0^\infty\int_{\mathbb{R}}e^{-i(t-T-\varphi(u))s}c_{x}(s)\,ds\int_{\mathsf{T_\varphi\mathcal Q_{k}}}b(\psi_0)e^{i\psi_0(u)-T(\operatorname{\mathrm{Hess}}_0\mathbf{Q}(\psi_0)/2+O(\|\psi_0\|^2))} \,d\psi_0\,dT \nonumber \\&\quad= \int_0^\infty \mathcal F c_{x}(t-T-\varphi(u))\int_{\mathsf{T_\varphi\mathcal Q_{k}}}b(\psi_0)e^{i\psi_0(u)-T(\operatorname{\mathrm{Hess}}_0\mathbf{Q}(\psi_0)/2+O(\|\psi_0\|^2))} \,d\psi_0\,dT \nonumber\\ &\quad= \int_{\varphi(u)}^\infty\mathcal F c_{x}(t-T)\int_{\mathsf{T_\varphi\mathcal Q_{k}}}b(\psi_0)e^{i\psi_0(u)-(T-\varphi(u))(\operatorname{\mathrm{Hess}}_0\mathbf{Q}(\psi_0)/2+O(\|\psi_0\|^2))} \,d\psi_0\,dT,\nonumber\\ &\quad=\int_{\max(t/2,\varphi(u))}^\infty\mathcal F c_{x}(t-T)\nonumber\\ &\ \qquad \times \int_{\mathsf{T_\varphi\mathcal Q_{k}}}b(\psi_0)e^{i\psi_0(u)-(T-\varphi(u))(\operatorname{\mathrm{Hess}}_0\mathbf{Q}(\psi_0)/2+O(\|\psi_0\|^2))} d\psi_0\,dT+O(t^{-N}), \end{align} $$
where the last equality is, as in [Reference Babillot and Ledrappier5, p. 27], essentially due to the fact that
![]() $c_x$
has compact support and is of class
$c_x$
has compact support and is of class
![]() $\operatorname {\mathrm {C}}^N.$
Applying the change of variables
$\operatorname {\mathrm {C}}^N.$
Applying the change of variables
![]() $\psi _0\mapsto \psi _0/\sqrt T$
, the last integral becomes
$\psi _0\mapsto \psi _0/\sqrt T$
, the last integral becomes
 $$ \begin{align}&\int_{\max(t/2,\varphi(u))}^\infty\frac{\mathcal F c_{x}(t-T)}{{\sqrt T}^{d-1}}\nonumber\\ &\quad\times \int_{\mathsf{T_\varphi\mathcal Q_{k}}}b\bigg(\frac{\psi_0}{\sqrt T}\bigg)e^{i({\psi_0}/{\sqrt T})(u)-(1-{\varphi(u)}/T)(\operatorname{\mathrm{Hess}}_0\mathbf{Q}(\psi_0)/2+O({\|\psi_0\|^2}/T))} d\psi_0\,dT+O(t^{-N}) \nonumber\\ &\quad=-\int_{-\infty}^{\min(t/2,t-\varphi(u))}\frac{\mathcal F c_{x}(S)}{{\sqrt{t-S}}^{d-1}}\int_{\mathsf{T_\varphi\mathcal Q_{k}}} b\bigg(\frac{\psi_0}{\sqrt{t-S}}\bigg)\nonumber\\ &\qquad \times e^{i({\psi_0}/{\sqrt{t-S}})(u)-(1-{\varphi(u)}/({t-S}))(\operatorname{\mathrm{Hess}}_0\mathbf{Q}(\psi_0)/2+O({\|\psi_0\|^2}/({t-S})))} \,d\psi_0\,dS+O(t^{-N}).\end{align} $$
$$ \begin{align}&\int_{\max(t/2,\varphi(u))}^\infty\frac{\mathcal F c_{x}(t-T)}{{\sqrt T}^{d-1}}\nonumber\\ &\quad\times \int_{\mathsf{T_\varphi\mathcal Q_{k}}}b\bigg(\frac{\psi_0}{\sqrt T}\bigg)e^{i({\psi_0}/{\sqrt T})(u)-(1-{\varphi(u)}/T)(\operatorname{\mathrm{Hess}}_0\mathbf{Q}(\psi_0)/2+O({\|\psi_0\|^2}/T))} d\psi_0\,dT+O(t^{-N}) \nonumber\\ &\quad=-\int_{-\infty}^{\min(t/2,t-\varphi(u))}\frac{\mathcal F c_{x}(S)}{{\sqrt{t-S}}^{d-1}}\int_{\mathsf{T_\varphi\mathcal Q_{k}}} b\bigg(\frac{\psi_0}{\sqrt{t-S}}\bigg)\nonumber\\ &\qquad \times e^{i({\psi_0}/{\sqrt{t-S}})(u)-(1-{\varphi(u)}/({t-S}))(\operatorname{\mathrm{Hess}}_0\mathbf{Q}(\psi_0)/2+O({\|\psi_0\|^2}/({t-S})))} \,d\psi_0\,dS+O(t^{-N}).\end{align} $$
We finally multiply by
![]() ${\sqrt t}^{d-1},$
take the limit as
${\sqrt t}^{d-1},$
take the limit as
![]() $t\to \infty $
, and trace back our definitions to get, as we assumed
$t\to \infty $
, and trace back our definitions to get, as we assumed
![]() $N>(d-1)/2,$
the convergence of equation (B.13) (and thus that of equation (B.10)) to
$N>(d-1)/2,$
the convergence of equation (B.13) (and thus that of equation (B.10)) to

where we have used equation (B.4) and the formula
![]() $\mathcal Fv_G(0)=\int _U v_G(u)\,du.$
Observe that, as
$\mathcal Fv_G(0)=\int _U v_G(u)\,du.$
Observe that, as
![]() $\operatorname {\mathrm {Hess}}_0\mathbf {Q}$
is positive-definite, the integral
$\operatorname {\mathrm {Hess}}_0\mathbf {Q}$
is positive-definite, the integral
![]() $\int _{\mathsf {T_\varphi \mathcal Q_{k}}}e^{-1/2\operatorname {\mathrm {Hess}}_0\mathbf {Q}(\psi _0)}\,d\psi _0$
is finite (and non-zero).
$\int _{\mathsf {T_\varphi \mathcal Q_{k}}}e^{-1/2\operatorname {\mathrm {Hess}}_0\mathbf {Q}(\psi _0)}\,d\psi _0$
is finite (and non-zero).
Remark B.4. If one modifies the action
![]() $(x,u)\mapsto (x,u-t\tau )$
to consider induction on the quotient by
$(x,u)\mapsto (x,u-t\tau )$
to consider induction on the quotient by
![]() $(x,u)\mapsto (x,u-t\tau -\sqrt t w_0)$
for a fixed
$(x,u)\mapsto (x,u-t\tau -\sqrt t w_0)$
for a fixed
![]() $w_0\in \ker \varphi $
, then tracing the computations, one readily sees that
$w_0\in \ker \varphi $
, then tracing the computations, one readily sees that

where we have defined
Observe that, as
![]() $\mathrm H(\psi _0)=\mathrm H(-\psi _0),$
the value of the Fourier transform
$\mathrm H(\psi _0)=\mathrm H(-\psi _0),$
the value of the Fourier transform
![]() $\mathcal F\mathrm H (w_0)\in \mathbb {R}.$
$\mathcal F\mathrm H (w_0)\in \mathbb {R}.$
We finally group back the equations to get the desired result. Indeed, equation (B.1) is

where we have used, in the first equality, equations (B.7) and (B.9) and the fact that
![]() $N>(1/2)(d-1)$
and, in the second equality, the convergence from equation (B.14). This completes the sketch of the proof.
$N>(1/2)(d-1)$
and, in the second equality, the convergence from equation (B.14). This completes the sketch of the proof.
Acknowledgements
This paper grew from a question asked to the author by Hee Oh on the ergodicity of directional flows for Anosov representations (now Theorem 5.12.1). The author would like to thank her for asking the question. He would also like to thank Marc Burger for encouraging him to pursue the ideas sketched on a very early version of this work, together with the remaining authors O. Landesberg, M. Lee, and H. Oh of the paper [Reference Burger, Landesberg, Lee and Oh20], whose results inspired Theorem B. A.S. was partially financed by ANR DynGeo ANR-16-CE40-0025.