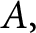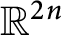Refine search
Actions for selected content:
19 results
15 - Historical Morphology
- from Part III - The Long View by Levels and Areas
-
-
- Book:
- The New Cambridge History of the English Language
- Published online:
- 30 October 2025
- Print publication:
- 30 October 2025, pp 468-544
-
- Chapter
- Export citation

Mathematics is (mostly) Analytic
-
- Published online:
- 09 January 2025
- Print publication:
- 30 January 2025
-
- Element
- Export citation
Existence and analyticity of solutions of the Kuramoto–Sivashinsky equation with singular data
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 20 November 2024, pp. 1-26
-
- Article
- Export citation
Analytic Cognition in Kant
-
- Journal:
- Kantian Review / Volume 29 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 09 September 2024, pp. 467-487
- Print publication:
- September 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Chapter 6 - On Quine’s Epistemological Objection to Carnap’s Analyticity
- from Part II - Naturalism and Method
-
-
- Book:
- Interpreting Carnap
- Published online:
- 01 February 2024
- Print publication:
- 08 February 2024, pp 106-126
-
- Chapter
- Export citation
Chapter 5 - Shades of Naturalism
- from Part II - Naturalism and Method
-
-
- Book:
- Interpreting Carnap
- Published online:
- 01 February 2024
- Print publication:
- 08 February 2024, pp 89-105
-
- Chapter
- Export citation
1 - “… I probably would never have written Structure”
- from Part I - Writing Structure
-
-
- Book:
- Kuhn's <i>The Structure of Scientific Revolutions</i> at 60
- Published online:
- 05 January 2024
- Print publication:
- 18 January 2024, pp 21-36
-
- Chapter
- Export citation
 $n$-coupling mechanisms are sufficient to obtain exponential decay in strain gradient elasticity
$n$-coupling mechanisms are sufficient to obtain exponential decay in strain gradient elasticity
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 34 / Issue 6 / December 2023
- Published online by Cambridge University Press:
- 22 May 2023, pp. 1288-1298
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
10 - Uncovering the Big Picture
-
-
- Book:
- English and Spanish
- Published online:
- 17 September 2021
- Print publication:
- 30 September 2021, pp 184-208
-
- Chapter
- Export citation
Derivatives of symplectic eigenvalues and a Lidskii type theorem
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 74 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 02 December 2020, pp. 457-485
- Print publication:
- April 2022
-
- Article
-
- You have access
- Export citation
23 - World Englishes from the Perspective of Dialect Typology
- from Part III - Linguistics and World Englishes
-
-
- Book:
- The Cambridge Handbook of World Englishes
- Published online:
- 16 December 2019
- Print publication:
- 02 January 2020, pp 534-558
-
- Chapter
- Export citation
12 - Spectrogram Geometry 2
- from Part II - Geometry and Statistics
-
- Book:
- Explorations in Time-Frequency Analysis
- Published online:
- 22 August 2018
- Print publication:
- 06 September 2018, pp 106-115
-
- Chapter
- Export citation
Logicism and Formal Necessity: Reflections on Kant’s Modal Metaphysics
-
- Journal:
- Kantian Review / Volume 23 / Issue 3 / September 2018
- Published online by Cambridge University Press:
- 21 August 2018, pp. 449-459
- Print publication:
- September 2018
-
- Article
- Export citation
On the Ornstein–Zernike equation for stationary cluster processes and the random connection model
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 49 / Issue 4 / December 2017
- Published online by Cambridge University Press:
- 17 November 2017, pp. 1260-1287
- Print publication:
- December 2017
-
- Article
- Export citation
Disquotational truth and analyticity
-
- Journal:
- The Journal of Symbolic Logic / Volume 66 / Issue 4 / December 2001
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1959-1973
- Print publication:
- December 2001
-
- Article
- Export citation
Analyticity of iterates of random non-expansive maps
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 32 / Issue 1 / March 2000
- Published online by Cambridge University Press:
- 01 July 2016, pp. 193-220
- Print publication:
- March 2000
-
- Article
- Export citation
Analytic controllability of the wave equationover a cylinder
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 4 / 1999
- Published online by Cambridge University Press:
- 15 August 2002, pp. 177-207
- Print publication:
- 1999
-
- Article
- Export citation
Expansions for Markov-modulated systems and approximations of ruin probability
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 33 / Issue 1 / March 1996
- Published online by Cambridge University Press:
- 14 July 2016, pp. 57-70
- Print publication:
- March 1996
-
- Article
- Export citation