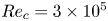Refine search
Actions for selected content:
256 results
On the stability and dynamics of flows past bubble-shaped rigid bluff bodies
-
- Journal:
- Journal of Fluid Mechanics / Volume 1025 / 25 December 2025
- Published online by Cambridge University Press:
- 12 December 2025, A5
-
- Article
- Export citation
A new upward-convective short-wave instability mode in gas-sheared falling liquid films
-
- Journal:
- Journal of Fluid Mechanics / Volume 1024 / 10 December 2025
- Published online by Cambridge University Press:
- 02 December 2025, A30
-
- Article
- Export citation
The effect of a forward-facing step on Tollmien–Schlichting waves
-
- Journal:
- Journal of Fluid Mechanics / Volume 1023 / 25 November 2025
- Published online by Cambridge University Press:
- 24 November 2025, A38
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Buoyancy-driven linear instability in a porous layer with contrasting heat sources
-
- Journal:
- Journal of Fluid Mechanics / Volume 1023 / 25 November 2025
- Published online by Cambridge University Press:
- 24 November 2025, A46
-
- Article
- Export citation
Characterisation of the secondary instability in a 1 : 3 sudden expansion through inviscid structural sensitivity
-
- Journal:
- Journal of Fluid Mechanics / Volume 1023 / 25 November 2025
- Published online by Cambridge University Press:
- 17 November 2025, A13
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Local and global instability of the rotating-disk boundary layer of a rotor-stator cavity
-
- Journal:
- Journal of Fluid Mechanics / Volume 1021 / 25 October 2025
- Published online by Cambridge University Press:
- 22 October 2025, A35
-
- Article
- Export citation
Instabilities in shock-wave–boundary-layer interactions at Mach 6
-
- Journal:
- Journal of Fluid Mechanics / Volume 1019 / 25 September 2025
- Published online by Cambridge University Press:
- 17 September 2025, A28
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Nonlinear dynamics of vortex pairing in transitional jets
-
- Journal:
- Journal of Fluid Mechanics / Volume 1018 / 10 September 2025
- Published online by Cambridge University Press:
- 04 September 2025, A32
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Characterising Görtler vortices in supersonic turbulent flows over concave surfaces
-
- Journal:
- Journal of Fluid Mechanics / Volume 1012 / 10 June 2025
- Published online by Cambridge University Press:
- 09 June 2025, A29
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Distribution of eigenfrequencies in long one-dimensional systems
-
- Journal:
- Journal of Fluid Mechanics / Volume 1010 / 10 May 2025
- Published online by Cambridge University Press:
- 28 April 2025, A9
-
- Article
- Export citation
Dynamics and 3-D instability of flow induced by the dielectric-barrier-discharge plasma actuator in an initially quiescent medium
-
- Journal:
- Journal of Fluid Mechanics / Volume 1008 / 10 April 2025
- Published online by Cambridge University Press:
- 10 April 2025, A50
-
- Article
- Export citation
On the linear stability of partially and fully saturated atmospheres to moist convection
-
- Journal:
- Journal of Fluid Mechanics / Volume 1007 / 25 March 2025
- Published online by Cambridge University Press:
- 17 March 2025, A60
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Absolute instability in the higher-generation airways: a pathway for airway closure
-
- Journal:
- Journal of Fluid Mechanics / Volume 1005 / 25 February 2025
- Published online by Cambridge University Press:
- 04 March 2025, A15
-
- Article
- Export citation
A long-wave model for a falling upper convected Maxwell film inside a tube
-
- Journal:
- Journal of Fluid Mechanics / Volume 1001 / 25 December 2024
- Published online by Cambridge University Press:
- 06 December 2024, A14
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Linear stability analysis of a vertical liquid film over a moving substrate
-
- Journal:
- Journal of Fluid Mechanics / Volume 1000 / 10 December 2024
- Published online by Cambridge University Press:
- 27 November 2024, A57
-
- Article
- Export citation
Transition to turbulence on a rotating wind turbine blade at
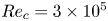 $Re_c=3 \times 10^5$
$Re_c=3 \times 10^5$
-
- Journal:
- Journal of Fluid Mechanics / Volume 999 / 25 November 2024
- Published online by Cambridge University Press:
- 14 November 2024, A54
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Influence of porous material on the flow behind a backward-facing step: experimental study
-
- Journal:
- Journal of Fluid Mechanics / Volume 998 / 10 November 2024
- Published online by Cambridge University Press:
- 31 October 2024, A31
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
One-winged butterflies: mode selection for azimuthal magnetorotational instability by thermal convection
-
- Journal:
- Journal of Fluid Mechanics / Volume 992 / 10 August 2024
- Published online by Cambridge University Press:
- 27 August 2024, R1
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The boundary layer instability beneath internal solitary waves and its sensitivity to vortex wakes
-
- Journal:
- Journal of Fluid Mechanics / Volume 990 / 10 July 2024
- Published online by Cambridge University Press:
- 14 August 2024, A18
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Non-Oberbeck–Boussinesq effects on the linear stability of a vertical natural convection boundary layer
-
- Journal:
- Journal of Fluid Mechanics / Volume 988 / 10 June 2024
- Published online by Cambridge University Press:
- 24 July 2024, A44
-
- Article
-
- You have access
- Open access
- HTML
- Export citation