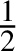Refine search
Actions for selected content:
7 results
Critical configurations of the hard-core model on square grid graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 34 / Issue 3 / May 2025
- Published online by Cambridge University Press:
- 04 February 2025, pp. 445-485
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Synchronization of coupled map lattices
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 30 March 2023, pp. 143-163
-
- Article
- Export citation
Soliton Decomposition of the Box-Ball System
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 03 September 2021, e60
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Comparison of Simulations of Convective Flows
-
- Journal:
- Communications in Computational Physics / Volume 17 / Issue 5 / May 2015
- Published online by Cambridge University Press:
- 03 June 2015, pp. 1169-1184
- Print publication:
- May 2015
-
- Article
- Export citation
On Triangular Lattice Boltzmann Schemes for Scalar Problems
-
- Journal:
- Communications in Computational Physics / Volume 13 / Issue 3 / March 2013
- Published online by Cambridge University Press:
- 03 June 2015, pp. 649-670
- Print publication:
- March 2013
-
- Article
- Export citation
Lattice Free Stochastic Dynamics
-
- Journal:
- Communications in Computational Physics / Volume 12 / Issue 3 / September 2012
- Published online by Cambridge University Press:
- 20 August 2015, pp. 691-702
- Print publication:
- September 2012
-
- Article
- Export citation
Replacement of train wheels: an application of dynamic reversal of a Markov process
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 31 / Issue 1 / March 1994
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1-8
- Print publication:
- March 1994
-
- Article
- Export citation