Refine search
Actions for selected content:
25 results
Density and unitarity of the Burau representation from a non-semisimple TQFT
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 28 July 2025, pp. 1-29
-
- Article
- Export citation
Constructing skew left braces whose additive group has trivial centre
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 30 January 2025, pp. 797-804
- Print publication:
- September 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
From actions of an abelian group on itself to left braces
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 178 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 09 January 2025, pp. 65-79
- Print publication:
- January 2025
-
- Article
- Export citation
Laurent family of simple modules over quiver Hecke algebras
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 8 / August 2024
- Published online by Cambridge University Press:
- 11 September 2024, pp. 1916-1940
- Print publication:
- August 2024
-
- Article
- Export citation
On the structure of some one-generator braces
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 2 / May 2024
- Published online by Cambridge University Press:
- 20 March 2024, pp. 566-576
-
- Article
- Export citation
Equivariant
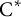 $\textrm {C}^*$-correspondences and compact quantum group actions on Pimsner algebras
$\textrm {C}^*$-correspondences and compact quantum group actions on Pimsner algebras
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 77 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 05 December 2023, pp. 57-96
- Print publication:
- February 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Comparison of quantizations of symmetric spaces: cyclotomic Knizhnik–Zamolodchikov equations and Letzter–Kolb coideals
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 11 / 2023
- Published online by Cambridge University Press:
- 02 May 2023, e14
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A Jordan–Hölder theorem for skew left braces and their applications to multipermutation solutions of the Yang–Baxter equation
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 24 April 2023, pp. 793-809
- Print publication:
- June 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Uniconnected solutions to the Yang–Baxter equation arising from self-maps of groups
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 20 April 2021, pp. 225-233
- Print publication:
- March 2022
-
- Article
- Export citation
One-generator braces and indecomposable set-theoretic solutions to the Yang–Baxter equation
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 63 / Issue 3 / August 2020
- Published online by Cambridge University Press:
- 06 May 2020, pp. 676-696
-
- Article
- Export citation
Laurent phenomenon and simple modules of quiver Hecke algebras
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 12 / December 2019
- Published online by Cambridge University Press:
- 04 October 2019, pp. 2263-2295
- Print publication:
- December 2019
-
- Article
- Export citation
QUANTUM INCREASING SEQUENCES GENERATE QUANTUM PERMUTATION GROUPS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 62 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 27 September 2019, pp. 631-639
- Print publication:
- September 2020
-
- Article
-
- You have access
- Export citation
Remarks on Hopf Images and Quantum Permutation Groups
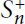 $S_{n}^{+}$
$S_{n}^{+}$
-
- Journal:
- Canadian Mathematical Bulletin / Volume 61 / Issue 2 / 01 June 2018
- Published online by Cambridge University Press:
- 20 November 2018, pp. 301-317
- Print publication:
- 01 June 2018
-
- Article
-
- You have access
- Export citation
Annular Khovanov homology and knotted Schur–Weyl representations
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 3 / March 2018
- Published online by Cambridge University Press:
- 28 November 2017, pp. 459-502
- Print publication:
- March 2018
-
- Article
- Export citation
A CATEGORIFICATION OF A QUANTUM FROBENIUS MAP
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 18 / Issue 5 / September 2019
- Published online by Cambridge University Press:
- 20 July 2017, pp. 899-939
- Print publication:
- September 2019
-
- Article
- Export citation
Simplicity of heads and socles of tensor products
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 2 / February 2015
- Published online by Cambridge University Press:
- 26 November 2014, pp. 377-396
- Print publication:
- February 2015
-
- Article
-
- You have access
- Export citation
A Remark on BMW Algebra, q-Schur Algebras and Categorification
-
- Journal:
- Canadian Journal of Mathematics / Volume 66 / Issue 2 / 01 April 2014
- Published online by Cambridge University Press:
- 20 November 2018, pp. 453-480
- Print publication:
- 01 April 2014
-
- Article
-
- You have access
- Export citation
Generating Functions for Hecke Algebra Characters
-
- Journal:
- Canadian Journal of Mathematics / Volume 63 / Issue 2 / 01 April 2011
- Published online by Cambridge University Press:
- 20 November 2018, pp. 413-435
- Print publication:
- 01 April 2011
-
- Article
-
- You have access
- Export citation
Commuting Families in Hecke and Temperley-Lieb Algebras
-
- Journal:
- Nagoya Mathematical Journal / Volume 195 / 2009
- Published online by Cambridge University Press:
- 11 January 2016, pp. 125-152
- Print publication:
- 2009
-
- Article
-
- You have access
- Export citation
Modified quantum dimensions and re-normalized link invariants
- Part of
-
- Journal:
- Compositio Mathematica / Volume 145 / Issue 1 / January 2009
- Published online by Cambridge University Press:
- 01 January 2009, pp. 196-212
- Print publication:
- January 2009
-
- Article
-
- You have access
- Export citation
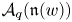
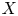
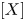
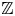

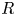
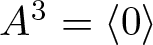
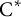





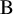
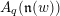
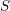
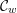
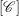
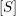
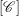
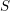
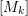
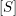
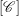
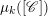
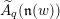
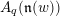
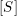
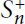
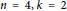
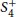
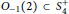
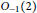
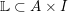
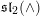
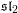
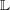
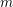

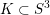
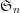
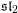
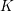

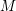
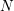
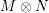
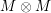

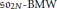


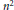
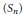
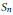
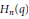
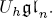 . We also give the explicit specializations of these results to the finite Temperley-Lieb algebra.
. We also give the explicit specializations of these results to the finite Temperley-Lieb algebra.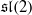 at a root of unity. These invariants contain Kashaev’s quantum dilogarithm invariants of knots.
at a root of unity. These invariants contain Kashaev’s quantum dilogarithm invariants of knots.