Refine search
Actions for selected content:
4 results
Time-dependent modelling of thin poroelastic films drying on deformable plates
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 35 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 12 April 2023, pp. 62-95
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Convergence of equilibria for bending-torsion models of rods with inhomogeneities
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 24 January 2019, pp. 233-260
- Print publication:
- February 2020
-
- Article
- Export citation
Nonlinear Vibration Analysis of Functionally Graded Nanobeam Using Homotopy Perturbation Method
- Part of
-
- Journal:
- Advances in Applied Mathematics and Mechanics / Volume 9 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 11 October 2016, pp. 144-156
- Print publication:
- February 2017
-
- Article
- Export citation
Toward a New Algorithm for Nonlinear Fractional Differential Equations
-
- Journal:
- Advances in Applied Mathematics and Mechanics / Volume 5 / Issue 2 / April 2013
- Published online by Cambridge University Press:
- 03 June 2015, pp. 222-234
- Print publication:
- April 2013
-
- Article
- Export citation

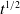
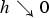
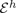 , for a rod
, for a rod 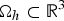
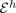 , provided that the bending energy of the sequence scales appropriately. This generalizes earlier results for homogeneous materials to the case of materials with (not necessarily periodic) inhomogeneities.
, provided that the bending energy of the sequence scales appropriately. This generalizes earlier results for homogeneous materials to the case of materials with (not necessarily periodic) inhomogeneities.