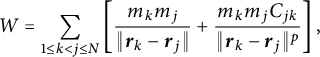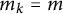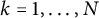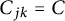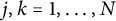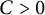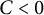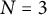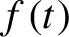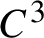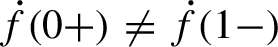Refine search
Actions for selected content:
7 results
Linear stability of the regular N-gon periodic solutions for the planar N-body problem with quasi-homogeneous potential
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 16 January 2025, pp. 1-25
-
- Article
- Export citation
Second-kind symmetric periodic orbits for planar perturbed Kepler problems and applications
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 19 May 2023, pp. 961-992
- Print publication:
- June 2024
-
- Article
- Export citation
Pseudo-holomorphic dynamics in the restricted three-body problem
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 174 / Issue 3 / May 2023
- Published online by Cambridge University Press:
- 05 December 2022, pp. 663-693
- Print publication:
- May 2023
-
- Article
- Export citation
A piecewise smooth Fermi–Ulam pingpong with potential
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 5 / May 2022
- Published online by Cambridge University Press:
- 04 March 2021, pp. 1847-1870
- Print publication:
- May 2022
-
- Article
- Export citation
On Moser’s regularization of the Kepler system: Positive and negative energies
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 18 December 2020, pp. 970-983
- Print publication:
- December 2021
-
- Article
- Export citation
Periodic Solutions of an Indefinite Singular Equation Arising from the Kepler Problemon the Sphere
-
- Journal:
- Canadian Journal of Mathematics / Volume 70 / Issue 1 / 01 February 2018
- Published online by Cambridge University Press:
- 20 November 2018, pp. 173-190
- Print publication:
- 01 February 2018
-
- Article
-
- You have access
- Export citation
Voronoi Domains and Dual Cells in the Generalized Kaleidoscope with Applications to Root and Weight Lattices
-
- Journal:
- Canadian Journal of Mathematics / Volume 47 / Issue 3 / 01 June 1995
- Published online by Cambridge University Press:
- 20 November 2018, pp. 573-605
- Print publication:
- 01 June 1995
-
- Article
-
- You have access
- Export citation