The method of equivariant moving frames is employed to construct and completely classify the differential invariants for the action of the projective group on functions defined on the two-dimensional projective plane. While there are four independent differential invariants of order $\leq 3$, it is proved that the algebra of differential invariants is generated by just two of them through invariant differentiation. The projective differential invariants are, in particular, of importance in image processing applications.

Image registration is the process of finding an alignment between two or more images so that their appearances match. It has been widely studied and applied to several fields, including medical imaging and biology, where it is related to morphometrics. In this paper, we present a construction of conformal diffeomorphisms which is based on constrained optimization. We consider a set of different penalty terms that aim to enforce conformality, based on discretizations of the Cauchy–Riemann equations and geometric principles, and demonstrate them experimentally on a variety of images.

Assignment flows denote a class of dynamical models for contextual data labelling (classification) on graphs. We derive a novel parametrisation of assignment flows that reveals how the underlying information geometry induces two processes for assignment regularisation and for gradually enforcing unambiguous decisions, respectively, that seamlessly interact when solving for the flow. Our result enables to characterise the dominant part of the assignment flow as a Riemannian gradient flow with respect to the underlying information geometry. We consider a continuous-domain formulation of the corresponding potential and develop a novel algorithm in terms of solving a sequence of linear elliptic partial differential equations (PDEs) subject to a simple convex constraint. Our result provides a basis for addressing learning problems by controlling such PDEs in future work.

Image feature points are detected as pixels which locally maximise a detector function, two commonly used examples of which are the (Euclidean) image gradient and the Harris–Stephens corner detector. A major limitation of these feature detectors is that they are only Euclidean-invariant. In this work, we demonstrate the application of a 2D equi-affine-invariant image feature point detector based on differential invariants as derived through the equivariant method of moving frames. The fundamental equi-affine differential invariants for 3D image volumes are also computed.

High order total variation (TV2) and ℓ1 based (TV2L1) model has its advantage over the TVL1 for its ability in avoiding the staircase; and a constrained model has the advantage over its unconstrained counterpart for simplicity in estimating the parameters. In this paper, we consider solving the TV2L1 based magnetic resonance imaging (MRI) signal reconstruction problem by an efficient alternating direction method of multipliers. By sufficiently utilizing the problem's special structure, we manage to make all subproblems either possess closed-form solutions or can be solved via Fast Fourier Transforms, which makes the cost per iteration very low. Experimental results for MRI reconstruction are presented to illustrate the effectiveness of the new model and algorithm. Comparisons with its recent unconstrained counterpart are also reported.

The hybrid variational model for restoration of texture images corrupted by blur and Gaussian noise we consider combines total variation regularisation and a fractional-order regularisation, and is solved by an alternating minimisation direction algorithm. Numerical experiments demonstrate the advantage of this model over the adaptive fractional-order variational model in image quality and computational time.

Multiplicative noise removal is a challenging problem in image restoration. In this paper, by applying Box-Cox transformation, we convert the multiplicative noise removal problem into the additive noise removal problem and the block matching three dimensional (BM3D) method is applied to get the final recovered image. Indeed, BM3D is an effective method to remove additive Gaussian white noise in images. A maximum likelihood method is designed to determine the parameter in the Box-Cox transformation. We also present the unbiased inverse transform for the Box-Cox transformation which is important. Both theoretical analysis and experimental results illustrate clearly that the proposed method can remove multiplicative noise very well especially when multiplicative noise is heavy. The proposed method is superior to the existing methods for multiplicative noise removal in the literature.

Recently, many variational models involving high order derivatives have been widely used in image processing, because they can reduce staircase effects during noise elimination. However, it is very challenging to construct efficient algorithms to obtain the minimizers of original high order functionals. In this paper, we propose a new linearized augmented Lagrangian method for Euler's elastica image denoising model. We detail the procedures of finding the saddle-points of the augmented Lagrangian functional. Instead of solving associated linear systems by FFT or linear iterative methods (e.g., the Gauss-Seidel method), we adopt a linearized strategy to get an iteration sequence so as to reduce computational cost. In addition, we give some simple complexity analysis for the proposed method. Experimental results with comparison to the previous method are supplied to demonstrate the efficiency of the proposed method, and indicate that such a linearized augmented Lagrangian method is more suitable to deal with large-sized images.

Amethod for non-rigid image registration that is suitable for large deformations is presented. Conventional registration methods embed the image in a B-spline object, and the image is evolved by deforming the B-spline object. In this work, we represent the image using B-spline and deform the image using a composition approach. We also derive a computationally efficient algorithm for calculating the B-spline coefficients and gradients of the image by adopting ideas from signal processing using image filters. We demonstrate the application of our method on several different types of 2D and 3D images and compare it with existing methods.

We propose a new two-phase method for reconstruction of blurred images corrupted by impulse noise. In the first phase, we use a noise detector to identify the pixels that are contaminated by noise, and then, in the second phase, we reconstruct the noisy pixels by solving an equality constrained total variation minimization problem that preserves the exact values of the noise-free pixels. For images that are only corrupted by impulse noise (i.e., not blurred) we apply the semismooth Newton's method to a reduced problem, and if the images are also blurred, we solve the equality constrained reconstruction problem using a first-order primal-dual algorithm. The proposed model improves the computational efficiency (in the denoising case) and has the advantage of being regularization parameter-free. Our numerical results suggest that the method is competitive in terms of its restoration capabilities with respect to the other two-phase methods.

Retinex theory explains how the human visual system perceives colors. The goal of retinex is to decompose the reflectance and the illumination from the given images and thereby compensating for non-uniform lighting. The existing methods for retinex usually use a single image with a fixed exposure to restore the reflectance of the image. In this paper, we propose a variational model for retinex problem by utilizing multi-exposure images of a given scene. The existence and uniqueness of the solutions of the proposed model have been elaborated. An alternating minimization method is constructed to solve the proposed model and its convergence is also demonstrated. The experimental results show that the proposed method is effective for reflectance recovery in retinex problem.

Mean curvature-based image registration model firstly proposed by Chumchob-Chen-Brito (2011) offered a better regularizer technique for both smooth and nonsmooth deformation fields. However, it is extremely challenging to solve efficiently this model and the existing methods are slow or become efficient only with strong assumptions on the smoothing parameter β. In this paper, we take a different solution approach. Firstly, we discretize the joint energy functional, following an idea of relaxed fixed point is implemented and combine with Gauss-Newton scheme with Armijo's Linear Search for solving the discretized mean curvature model and further to combine with a multilevel method to achieve fast convergence. Numerical experiments not only confirm that our proposed method is efficient and stable, but also it can give more satisfying registration results according to image quality.

Image segmentation is a fundamental problem in both image processing and computer vision with numerous applications. In this paper, we propose a two-stage image segmentation scheme based on inexact alternating direction method. Specifically, we first solve the convex variant of the Mumford-Shah model to get the smooth solution, the segmentation are then obtained by apply the K-means clustering method to the solution. Some numerical comparisons are arranged to show the effectiveness of our proposed schemes by segmenting many kinds of images such as artificial images, natural images, and brain MRI images.

In this paper we consider an anisotropic convection-diffusion (ACD) filter for image denoising and compression simultaneously. The ACD filter is discretized by a tailored finite point method (TFPM), which can tailor some particular properties of the image in an irregular grid structure. A quadtree structure is implemented for the storage in multi-levels for the compression. We compare the performance of the proposed scheme with several well-known filters. The numerical results show that the proposed method is effective for removing a mixture of white Gaussian and salt-and-pepper noises.

Image registration is an ill-posed problem that has been studied widely in recent years. The so-called curvature-based image registration method is one of the most effective and well-known approaches, as it produces smooth solutions and allows an automatic rigid alignment. An important outstanding issue is the accurate and efficient numerical solution of the Euler-Lagrange system of two coupled nonlinear biharmonic equations, addressed in this article. We propose a fourth-order compact (FOC) finite difference scheme using a splitting operator on a 9-point stencil, and discuss how the resulting nonlinear discrete system can be solved efficiently by a nonlinear multi-grid (NMG) method. Thus after measuring the h-ellipticity of the nonlinear discrete operator involved by a local Fourier analysis (LFA), we show that our FOC finite difference method is amenable to multi-grid (MG) methods and an appropriate point-wise smoothing procedure. A high potential point-wise smoother using an outer-inner iteration method is shown to be effective by the LFA and numerical experiments. Real medical images are used to compare the accuracy and efficiency of our approach and the standard second-order central (SSOC) finite difference scheme in the same NMG framework. As expected for a higher-order finite difference scheme, the images generated by our FOC finite difference scheme prove significantly more accurate than those computed using the SSOC finite difference scheme. Our numerical results are consistent with the LFA analysis, and also demonstrate that the NMG method converges within a few steps.

Algebraic Multigrid (AMG) methods were developed originally for numerically solving Partial Differential Equations (PDE), not necessarily on structured grids. In the last two decades solvers inspired by the AMG approach, were developed for non PDE problems, including data and image analysis problems, such as clustering, segmentation, quantization and others. These solvers share a common principle in that there is a crosstalk between fine and coarse representations of the problems, with flow of information in both directions, fine-to-coarse and coarse-to-fine. This paper surveys some of these problems and the AMG-inspired algorithms for their solution.

Denoising of images corrupted by multiplicative noise is an important task in various applications, such as laser imaging, synthetic aperture radar and ultrasound imaging. We propose a combined first-order and second-order variational model for removal of multiplicative noise. Our model substantially reduces the staircase effects while preserving edges in the restored images, since it combines advantages of the first-order and second-order total variation. The issues of existence and uniqueness of a minimizer for this variational model are analysed. Moreover, a gradient descent method is employed to solve the associated Euler–Lagrange equation, and several numerical experiments are given to show the efficiency of our model. In particular, a comparison with an existing model in terms of peak signal-to-noise ratio and structural similarity index is provided.

In this paper, we study to use nonlocal bounded variation (NLBV) techniques to decompose an image intensity into the illumination and reflectance components. By considering spatial smoothness of the illumination component and nonlocal total variation (NLTV) of the reflectance component in the decomposition framework, an energy functional is constructed. We establish the theoretical results of the space of NLBV functions such as lower semicontinuity, approximation and compactness. These essential properties of NLBV functions are important tools to show the existence of solution of the proposed energy functional. Experimental results on both grey-level and color images are shown to illustrate the usefulness of the nonlocal total variation image decomposition model, and demonstrate the performance of the proposed method is better than the other testing methods.

Image fusion is an imaging technique to visualize information from multiple imaging sources in one single image, which is widely used in remote sensing, medical imaging etc. In this work, we study two variational approaches to image fusion which are closely related to the standard TV-L2 and TV-L1 image approximation methods. We investigate their convex optimization formulations, under the perspective of primal and dual, and propose their associated new image decomposition models. 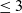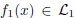In addition, we consider the TV-L1 based image fusion approach and study the specified problem of fusing two discrete-constrained images and 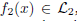where 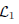and 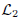are the sets of linearly-ordered discrete values. We prove that the TV-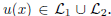L1 based image fusion actually gives rise to the exact convex relaxation to the corresponding nonconvex image fusion constrained by the discrete-valued set This extends the results for the global optimization of the discrete-constrained TV-L1 image approximation [8, 36] to the case of image fusion. As a big numerical advantage of the two proposed dual models, we show both of them directly lead to new fast and reliable algorithms, based on modern convex optimization techniques. Experiments with medical images, remote sensing images and multi-focus images visibly show the qualitative differences between the two studied variational models of image fusion. We also apply the new variational approaches to fusing 3D medical images.

We present a multi-phase image segmentation method based on the histogram of the Gabor feature space, which consists of a set of Gabor-filter responses with various orientations, scales and frequencies. Our model replaces the error function term in the original fuzzy region competition model with squared 2-Wasserstein distance function, which is a metric to measure the distance of two histograms. The energy functional is minimized by alternative minimization method and the existence of closed-form solutions is guaranteed when the exponent of the fuzzy membership term being 1 or 2. We test our model on both simple synthetic texture images and complex natural images with two or more phases. Experimental results are shown and compared to other recent results.