Refine search
Actions for selected content:
20 results
IMPLICIT–EXPLICIT TIME INTEGRATION METHOD FOR FRACTIONAL ADVECTION–DIFFUSION-REACTION EQUATIONS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 67 / 2025
- Published online by Cambridge University Press:
- 16 October 2024, e2
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
MONTE CARLO VARIANCE REDUCTION METHODS WITH APPLICATIONS IN STRUCTURAL RELIABILITY ANALYSIS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 3 / December 2023
- Published online by Cambridge University Press:
- 31 August 2023, pp. 518-521
- Print publication:
- December 2023
-
- Article
-
- You have access
- HTML
- Export citation
CONFIDENCE INTERVALS IN GENERAL REGRESSION MODELS THAT UTILISE UNCERTAIN PRIOR INFORMATION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 3 / June 2022
- Published online by Cambridge University Press:
- 08 February 2022, pp. 516-517
- Print publication:
- June 2022
-
- Article
-
- You have access
- HTML
- Export citation
Asymptotic variance of Newton–Cotes quadratures based on randomized sampling points
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 52 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 03 December 2020, pp. 1284-1307
- Print publication:
- December 2020
-
- Article
- Export citation
IMPLEMENTATION OF HIGH-ORDER, DISCONTINUOUS GALERKIN TIME STEPPING FOR FRACTIONAL DIFFUSION PROBLEMS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 62 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 06 November 2020, pp. 121-147
-
- Article
-
- You have access
- Export citation
Structure-Preserving Wavelet Algorithms for the Nonlinear Dirac Model
- Part of
-
- Journal:
- Advances in Applied Mathematics and Mechanics / Volume 9 / Issue 4 / August 2017
- Published online by Cambridge University Press:
- 18 January 2017, pp. 964-989
- Print publication:
- August 2017
-
- Article
- Export citation
A New Quasi-Monte Carlo Technique Based on Nonnegative Least Squares and Approximate Fekete Points
- Part of
-
- Journal:
- Numerical Mathematics: Theory, Methods and Applications / Volume 9 / Issue 4 / November 2016
- Published online by Cambridge University Press:
- 17 November 2016, pp. 640-663
- Print publication:
- November 2016
-
- Article
- Export citation
A Simple Method for Computing Singular or Nearly Singular Integrals on Closed Surfaces
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 20 / Issue 3 / September 2016
- Published online by Cambridge University Press:
- 31 August 2016, pp. 733-753
- Print publication:
- September 2016
-
- Article
- Export citation
Simple Fourth-Degree Cubature Formulae with Few Nodes over General Product Regions
-
- Journal:
- Numerical Mathematics: Theory, Methods and Applications / Volume 7 / Issue 2 / May 2014
- Published online by Cambridge University Press:
- 28 May 2015, pp. 179-192
- Print publication:
- May 2014
-
- Article
- Export citation
Random Construction of Interpolating Sets for High-Dimensional Integration
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 51 / Issue 1 / March 2014
- Published online by Cambridge University Press:
- 30 January 2018, pp. 92-105
- Print publication:
- March 2014
-
- Article
-
- You have access
- Export citation
GEGENBAUER COLLOCATION INTEGRATION METHODS: ADVANCES IN COMPUTATIONAL OPTIMAL CONTROL THEORY
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 89 / Issue 1 / February 2014
- Published online by Cambridge University Press:
- 05 February 2014, pp. 168-170
- Print publication:
- February 2014
-
- Article
-
- You have access
- Export citation
A Parallel Adaptive Treecode Algorithm for Evolution of Elastically Stressed Solids
-
- Journal:
- Communications in Computational Physics / Volume 15 / Issue 2 / February 2014
- Published online by Cambridge University Press:
- 03 June 2015, pp. 365-387
- Print publication:
- February 2014
-
- Article
- Export citation
Numerical Integration over Pyramids
-
- Journal:
- Advances in Applied Mathematics and Mechanics / Volume 5 / Issue 3 / June 2013
- Published online by Cambridge University Press:
- 03 June 2015, pp. 309-320
- Print publication:
- June 2013
-
- Article
- Export citation
Convergent Overdetermined-RBF-MLPG for Solving Second Order Elliptic PDEs
-
- Journal:
- Advances in Applied Mathematics and Mechanics / Volume 5 / Issue 1 / February 2013
- Published online by Cambridge University Press:
- 03 June 2015, pp. 78-89
- Print publication:
- February 2013
-
- Article
- Export citation
Fluxon Centering in Josephson Junctions with Exponentially Varying Width
-
- Journal:
- East Asian Journal on Applied Mathematics / Volume 2 / Issue 3 / August 2012
- Published online by Cambridge University Press:
- 28 May 2015, pp. 204-213
- Print publication:
- August 2012
-
- Article
- Export citation
The Eulerian-Lagrangian Method with Accurate Numerical Integration
-
- Journal:
- Advances in Applied Mathematics and Mechanics / Volume 4 / Issue 2 / April 2012
- Published online by Cambridge University Press:
- 03 June 2015, pp. 156-174
- Print publication:
- April 2012
-
- Article
- Export citation
Orthogonal Polynomials with Respect to Modified Jacobi Weight and Corresponding Quadrature Rules of Gaussian Type
-
- Journal:
- Numerical Mathematics: Theory, Methods and Applications / Volume 4 / Issue 4 / November 2011
- Published online by Cambridge University Press:
- 28 May 2015, pp. 478-488
- Print publication:
- November 2011
-
- Article
- Export citation
Approximations of boundary crossing probabilities for a Brownian motion
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 36 / Issue 4 / December 1999
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1019-1030
- Print publication:
- December 1999
-
- Article
- Export citation
Stereological estimation of particle size distributions
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 27 / Issue 2 / June 1995
- Published online by Cambridge University Press:
- 01 July 2016, pp. 350-366
- Print publication:
- June 1995
-
- Article
- Export citation
Hermite and Hermite-Fejer Interpolation and Associated Product Integration Rules on the Real Line: The L 1 Theory
-
- Journal:
- Canadian Journal of Mathematics / Volume 44 / Issue 3 / 01 June 1992
- Published online by Cambridge University Press:
- 20 November 2018, pp. 561-590
- Print publication:
- 01 June 1992
-
- Article
-
- You have access
- Export citation
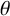
 ) and the Zimm chain solution (
) and the Zimm chain solution ( ). Numerical simulations of the viscoelastic channel flow effectively capture the nonhomogeneous regions of high viscosity at low fluid inertia (or the so-called “spatiotemporal macrostructures”), experimentally observed in the flow-instability transition of subdiffusive flows.
). Numerical simulations of the viscoelastic channel flow effectively capture the nonhomogeneous regions of high viscosity at low fluid inertia (or the so-called “spatiotemporal macrostructures”), experimentally observed in the flow-instability transition of subdiffusive flows.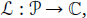 defined on the space of all algebraic polynomials
defined on the space of all algebraic polynomials 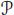 by
by