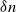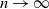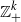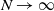Refine search
Actions for selected content:
244 results
Colored interacting particle systems on the ring: Stationary measures from Yang–Baxter equations
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 8 / August 2025
- Published online by Cambridge University Press:
- 03 October 2025, pp. 1855-1922
- Print publication:
- August 2025
-
- Article
- Export citation
Optimal stopping zero-sum games in continuous hidden Markov models
- Part of
-
- Journal:
- Advances in Applied Probability , First View
- Published online by Cambridge University Press:
- 28 July 2025, pp. 1-44
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Cutoff for the logistic SIS epidemic model with self-infection
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 57 / Issue 4 / December 2025
- Published online by Cambridge University Press:
- 04 June 2025, pp. 1456-1483
- Print publication:
- December 2025
-
- Article
- Export citation
Stationary measures of continuous-time Markov chains with applications to stochastic reaction networks
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 57 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 14 May 2025, pp. 1031-1067
- Print publication:
- September 2025
-
- Article
- Export citation
Phase-type representations for exponential distributions
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 57 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 04 March 2025, pp. 969-999
- Print publication:
- September 2025
-
- Article
- Export citation
A non-convex optimization approach of searching algebraic degree phase-type representations for general phase-type distributions
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 57 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 03 March 2025, pp. 1101-1137
- Print publication:
- September 2025
-
- Article
- Export citation
Asymptotic expansion of the invariant measure for Markov-modulated ODEs at high frequency
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 62 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 30 January 2025, pp. 898-924
- Print publication:
- September 2025
-
- Article
- Export citation
Mean-field analysis of stochastic networks with reservation
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 62 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 06 January 2025, pp. 832-858
- Print publication:
- June 2025
-
- Article
- Export citation
The Markov chain embedding problem in a one-jump setting
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 62 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 09 December 2024, pp. 674-696
- Print publication:
- June 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Error bounds for one-dimensional constrained Langevin approximations for nearly density-dependent Markov chains
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 56 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 26 July 2024, pp. 825-867
- Print publication:
- September 2024
-
- Article
- Export citation
Perturbation analysis for continuous-time Markov chains in a weak sense
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 13 May 2024, pp. 1278-1300
- Print publication:
- December 2024
-
- Article
- Export citation
A large-deviation principle for birth–death processes with a linear rate of downward jumps
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 31 October 2023, pp. 781-801
- Print publication:
- September 2024
-
- Article
- Export citation
The asymptotic tails of limit distributions of continuous-time Markov chains
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 56 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 06 October 2023, pp. 693-734
- Print publication:
- June 2024
-
- Article
- Export citation
Comparison theorem and stability under perturbation of transition rate matrices for regime-switching processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 14 September 2023, pp. 540-557
- Print publication:
- June 2024
-
- Article
- Export citation
Strong convergence of an epidemic model with mixing groups
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 56 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 01 September 2023, pp. 430-463
- Print publication:
- June 2024
-
- Article
- Export citation
Improved Metropolis–Hastings algorithms via landscape modification with applications to simulated annealing and the Curie–Weiss model
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 56 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 30 August 2023, pp. 587-620
- Print publication:
- June 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Propagation of chaos and large deviations in mean-field models with jumps on block-structured networks
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 55 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 05 June 2023, pp. 1301-1361
- Print publication:
- December 2023
-
- Article
- Export citation
Asymptotic persistence time formulae for multitype birth–death processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 21 March 2023, pp. 895-920
- Print publication:
- September 2023
-
- Article
- Export citation
Moran models and Wright–Fisher diffusions with selection and mutation in a one-sided random environment
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 55 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 09 March 2023, pp. 701-767
- Print publication:
- September 2023
-
- Article
- Export citation
Sturm–Liouville theory and decay parameter for quadratic markov branching processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 19 January 2023, pp. 737-764
- Print publication:
- September 2023
-
- Article
- Export citation